Model Combinations
through revised
base rates
Anastasios Panagiotelis
University of Sydney
1
Co-authors
 Fotios Petropoulos
Fotios Petropoulos

Evangelos Spiliotis
2
A motivation
3
A problem for undergrads
- An algorithm detects fraud
4
A problem for undergrads
- An algorithm detects fraud
- The algorithm has an accuracy of 90%
4
A problem for undergrads
- An algorithm detects fraud
- The algorithm has an accuracy of 90%
- If fraud is committed the algorithm detects fraud 90% of the time
4
A problem for undergrads
- An algorithm detects fraud
- The algorithm has an accuracy of 90%
- If fraud is committed the algorithm detects fraud 90% of the time
- If fraud is not committed the algorithm detects no fraud 90% of the time.
4
A problem for undergrads
- An algorithm detects fraud
- The algorithm has an accuracy of 90%
- If fraud is committed the algorithm detects fraud 90% of the time
- If fraud is not committed the algorithm detects no fraud 90% of the time.
- You apply the algorithm to an individual and the algorithm detects fraud.
- What is the probability that the individual has truly committed fraud?
4
A problem for forecasters
- An information criterion (IC) selects whether a forecasting model is 'correct'.
- The (IC) has an accuracy of 90%
- If model truly correct the IC selects it 90% of the time
- If model is not truly correct, the algorithm selects another model 90% of the time.
- You apply the IC to a time series and the algorithm selects the model.
- What is the probability that selected model is the correct model?
5
Setting
- Setting is multivariate data
6
Setting
- Setting is multivariate data
- Macroeconomics (FRED data)
- Retail (SKU)
- M forecasting competitions
6
Setting
- Setting is multivariate data
- Macroeconomics (FRED data)
- Retail (SKU)
- M forecasting competitions
- Will focus on univariate models however...
6
Setting
- Setting is multivariate data
- Macroeconomics (FRED data)
- Retail (SKU)
- M forecasting competitions
- Will focus on univariate models however...
- ... still want to cross learn.
6
Setting
- Setting is multivariate data
- Macroeconomics (FRED data)
- Retail (SKU)
- M forecasting competitions
- Will focus on univariate models however...
- ... still want to cross learn.
- Can the behavior of selection criteria across a set of 'reference' series improve forecast selection and combination?
6
The method
7
Selected and Correct
- Information criteria include AIC and BIC
- "Correct" model is one that minimises forecast error (MAE or RMSE)
- Construct a contingency table of selected/correct models.
- Compute the following probabilities
- p(C|S): Precision
- p(S|C): Sensitivity
- Sensitivity = Precision if all models are equally likely to be the correct model a priori.
8
Computing the Table
- Fit all models
9
Computing the Table
- Fit all models
- Compute selection criterion
- Determine selected model
9
Computing the Table
- Fit all models
- Compute selection criterion
- Determine selected model
- Forecast using all models
9
Computing the Table
- Fit all models
- Compute selection criterion
- Determine selected model
- Forecast using all models
- Evaluate out of sample criterion
- Determine "correct" model
9
Computing the Table
- Fit all models
- Compute selection criterion
- Determine selected model
- Forecast using all models
- Evaluate out of sample criterion
- Determine "correct" model
- Repeat for all series
9
(Part of) a cross tab
| ARMA(1,1) | SAR(1) | SMA(1) | Total | |
|---|---|---|---|---|
| ARMA(1,1) | 25 | 0 | 1 | 26 |
| SAR(1) | 0 | 34 | 2 | 36 |
| SMA(1) | 0 | 7 | 0 | 7 |
| Total | 25 | 41 | 3 | 69 |
- This is a simulation where all series are ARMA(1,1) or SAR(1).
- Sometimes we select SMA(1), but cross learning leads the correct model.
10
Precision
| ARMA(1,1) | SAR(1) | SMA(1) | Total | |
|---|---|---|---|---|
| ARMA(1,1) | 25 | 0 | 1 | 26 |
| SAR(1) | 0 | 34 | 2 | 36 |
| SMA(1) | 0 | 7 | 0 | 7 |
| Total | 25 | 41 | 3 | 69 |
11
Precision
| ARMA(1,1) | SAR(1) | SMA(1) | Total | |
|---|---|---|---|---|
| ARMA(1,1) | 25 | 0 | 1 | 26 |
| SAR(1) | 0 | 34 | 2 | 36 |
| SMA(1) | 0 | 7 | 0 | 7 |
| Total | 25 | 41 | 3 | 69 |
- Suppose SAR(1) selected.
- Consider one row and normalise.
- Weights w=(0, 0.944, 0.056) proxy p(C|S).
11
Sensitivity
| ARMA(1,1) | SAR(1) | SMA(1) | Total | |
|---|---|---|---|---|
| ARMA(1,1) | 25 | 0 | 1 | 26 |
| SAR(1) | 0 | 34 | 2 | 36 |
| SMA(1) | 0 | 7 | 0 | 7 |
| Total | 25 | 41 | 3 | 69 |
12
Sensitivity
| ARMA(1,1) | SAR(1) | SMA(1) | Total | |
|---|---|---|---|---|
| ARMA(1,1) | 25 | 0 | 1 | 26 |
| SAR(1) | 0 | 34 | 2 | 36 |
| SMA(1) | 0 | 7 | 0 | 7 |
| Total | 25 | 41 | 3 | 69 |
- Apply Bayes' Rule to get p(S|C)
12
Sensitivity
| ARMA(1,1) | SAR(1) | SMA(1) | Total | |
|---|---|---|---|---|
| ARMA(1,1) | 25 | 0 | 1 | 26 |
| SAR(1) | 0 | 34 | 2 | 36 |
| SMA(1) | 0 | 7 | 0 | 7 |
| Total | 25 | 41 | 3 | 69 |
- Apply Bayes' Rule to get p(S|C)
- If SAR(1) selected w=(0, 0.554, 0.446)
12
Sensitivity
| ARMA(1,1) | SAR(1) | SMA(1) | Total | |
|---|---|---|---|---|
| ARMA(1,1) | 25 | 0 | 1 | 26 |
| SAR(1) | 0 | 34 | 2 | 36 |
| SMA(1) | 0 | 7 | 0 | 7 |
| Total | 25 | 41 | 3 | 69 |
- Apply Bayes' Rule to get p(S|C)
- If SAR(1) selected w=(0, 0.554, 0.446)
- May be useful if assume uniform priors of 'correct' model for new series
12
Applications
13
Fred data
- Consider monthly FRED data (Ng and McCracken data).
14
Fred data
- Consider monthly FRED data (Ng and McCracken data).
- Forecast 115 series.
14
Fred data
- Consider monthly FRED data (Ng and McCracken data).
- Forecast 115 series.
- Use a training sample of T=60 and rolling window of length Win=30 to construct cross tab.
14
Fred data
- Consider monthly FRED data (Ng and McCracken data).
- Forecast 115 series.
- Use a training sample of T=60 and rolling window of length Win=30 to construct cross tab.
- Then wrap this inside another rolling window of size Wout=90.
14
Fred data
- Consider monthly FRED data (Ng and McCracken data).
- Forecast 115 series.
- Use a training sample of T=60 and rolling window of length Win=30 to construct cross tab.
- Then wrap this inside another rolling window of size Wout=90.
- Evaluation based on MASE.
14
Fred data
- Consider monthly FRED data (Ng and McCracken data).
- Forecast 115 series.
- Use a training sample of T=60 and rolling window of length Win=30 to construct cross tab.
- Then wrap this inside another rolling window of size Wout=90.
- Evaluation based on MASE.
- Consider 16 (Seasonal) ARMA models
14
Benchmarks
- Selection
- Best model according to criterion (criterion-select)
- Most common correct model overall (aggregate-select)
15
Benchmarks
- Selection
- Best model according to criterion (criterion-select)
- Most common correct model overall (aggregate-select)
- Combination
- Equal weights
- Criterion specific weights wi∝exp(Si)
- Regularised weights (Diebold and Shin, 2019)
15
Selection Results
| Method | MASE |
|---|---|
| Aggregate-Select | 0.553 |
| Criterion-Select | 0.530 |
| Precision-Select | 0.537 |
| Sensitivity-Select | 0.544 |
16
Combination Results
| Method | MASE |
|---|---|
| Equal | 0.532 |
| Regularised | 0.533 |
| Criterion-Average | 0.527 |
| Precision-Average | 0.525 |
| Sensitivity-Average | 0.527 |
For combination in this example, cross learning can help.
17
M Competition
- Data from M, M3 and M4.
18
M Competition
- Data from M, M3 and M4.
- Yearly, Quarterly and Monthly frequency.
18
M Competition
- Data from M, M3 and M4.
- Yearly, Quarterly and Monthly frequency.
- Consider 15 clases of ETS model.
18
M Competition
- Data from M, M3 and M4.
- Yearly, Quarterly and Monthly frequency.
- Consider 15 clases of ETS model.
- Total of 95,434 series.
18
Selection Results
| Method | Yearly | Quarterly | Monthly |
|---|---|---|---|
| Aggregate-Select | 3.512 | 1.192 | 0.988 |
| Criterion-Select | 3.412 | 1.166 | 0.949 |
| Precision-Select | 3.490 | 1.184 | 0.985 |
| Sensitivity-Select | 3.309 | 1.174 | 0.948 |
19
Combination Results
| Method | Yearly | Quarterly | Monthly |
|---|---|---|---|
| Equal | 3.231 | 1.174 | 0.948 |
| Criterion-Average | 3.351 | 1.152 | 0.942 |
| Precision-Average | 3.247 | 1.147 | 0.160 |
| Sensitivity-Average | 3.212 | 1.155 | 0.922 |
For combination in this example, cross learning helps at all frequencies.
20
Size of Reference Set
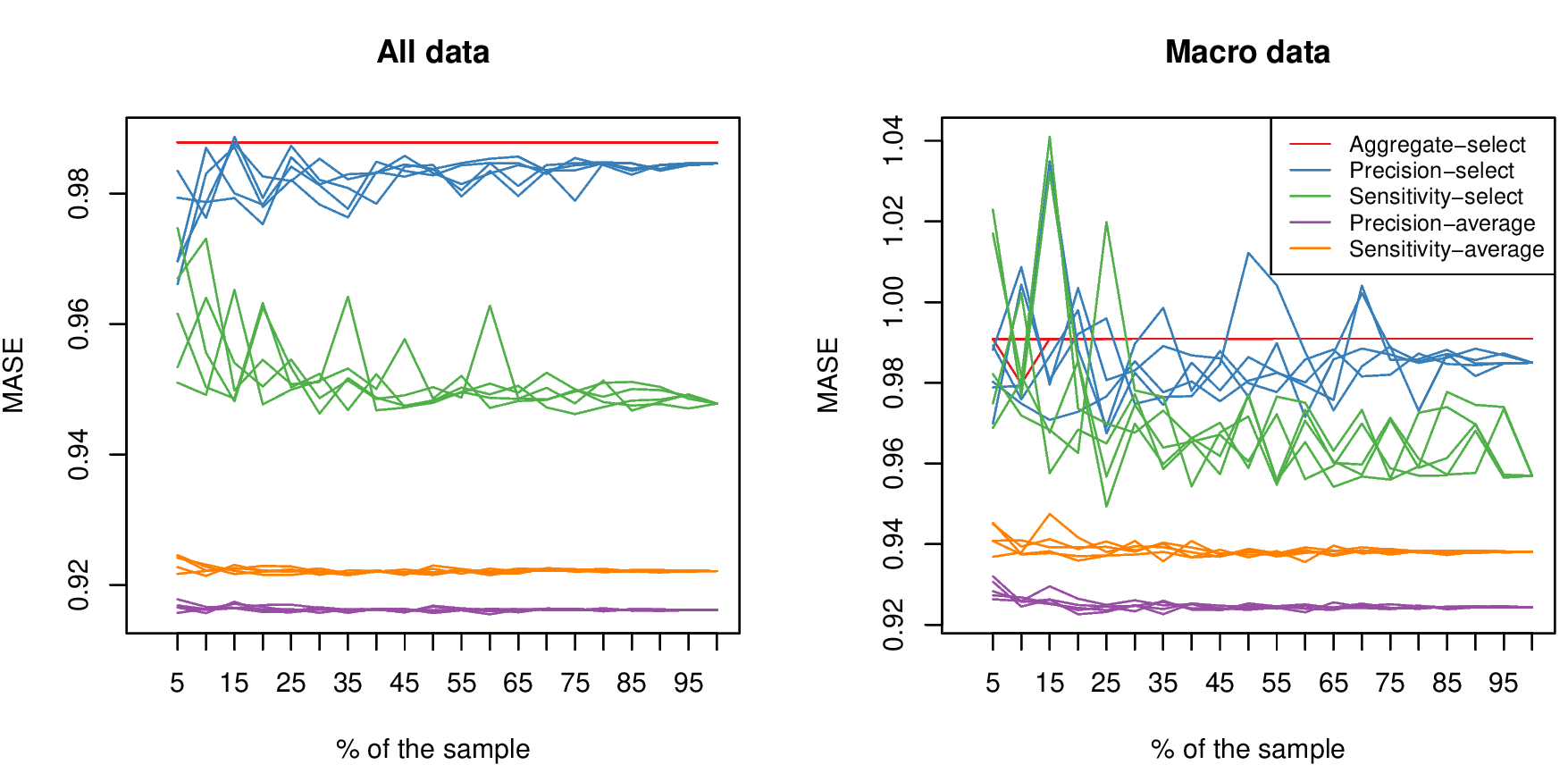
21
Conclusions
- This is a simple way to do cross learning.
22
Conclusions
- This is a simple way to do cross learning.
- Can achieve modest gains for a small number of variables (~100).
22
Conclusions
- This is a simple way to do cross learning.
- Can achieve modest gains for a small number of variables (~100).
- For 1k-100k variables, our combinations methods are
- Outperforming benchmarks,
- Better than corresponding selection methods and
- Robust to size and choice of 'reference' set
22
Questions ?
23