Reconciliation
 with Immutable
 Forecasts
Anastasios Panagiotelis
December 1, 2022
1

Joint work with

Bohan Zhang

Joint work with

Bohan Zhang

Yanfei Kang

Joint work with

Bohan Zhang

Yanfei Kang

Feng Li

Reconciliation background3

Hierarchical Time SeriesMultivariate forecasting problem.
4

Hierarchical Time SeriesMultivariate forecasting problem.
Variables follow linear constraints.
4

Hierarchical Time SeriesMultivariate forecasting problem.
Variables follow linear constraints.
Forecast store level sales and aggregates.
4

Problem contextHave base forecasts at all nodes. How can we make these coherent?
5

Problem contextHave base forecasts at all nodes. How can we make these coherent?
Bottom Up (Schwarzkopf, Tersine, and Morris, 1988) ignores top nodes.
5

Problem contextHave base forecasts at all nodes. How can we make these coherent?
Bottom Up (Schwarzkopf, Tersine, and Morris, 1988) ignores top nodes.  Noise in bottom level transferred to top level.

5

Problem contextHave base forecasts at all nodes. How can we make these coherent?
Bottom Up (Schwarzkopf, Tersine, and Morris, 1988) ignores top nodes.  Noise in bottom level transferred to top level.  

Top Down (Gross and Sohl, 1990) ignores bottom nodes.
5

Problem contextHave base forecasts at all nodes. How can we make these coherent?
Bottom Up (Schwarzkopf, Tersine, and Morris, 1988) ignores top nodes.  Noise in bottom level transferred to top level.  

Top Down (Gross and Sohl, 1990) ignores bottom nodes.Discards information.
Can bias even unbiased base forecasts.

5

ReconciliationBase forecasts stacked in an nn-vector ^yy^.
6

ReconciliationBase forecasts stacked in an nn-vector ^yy^.
Reconciled forecasts ~yy~ given by
~y=S(S′WS)−1S′W^yy~=S(S′WS)−1S′Wy^
6

ReconciliationBase forecasts stacked in an nn-vector ^yy^.
Reconciled forecasts ~yy~ given by
~y=S(S′WS)−1S′W^yy~=S(S′WS)−1S′Wy^
Different choices of WWWW give rise to different methods.
6

ReconciliationBase forecasts stacked in an nn-vector ^yy^.
Reconciled forecasts ~yy~ given by
~y=S(S′WS)−1S′W^yy~=S(S′WS)−1S′Wy^
Different choices of WWWW give rise to different methods.
The original is WW=IIWW=II (Hyndman, Ahmed, Athanasopoulos, and Shang, 2011).
6

What is $S S$ ?

$y y = S S b b$

What is $S S$ ?

$y y = S S b b$

$S = (\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$

Why optimal? Minimises expected loss

MinT method (Wickramasuriya, Athanasopoulos, and Hyndman, 2019) minimises

$E [(y y - \tilde{y y})^{'} (y y - \tilde{y y})]$

if $W W$ is set to the inverse forecast error covariance of the base forecasts.

Why optimal? Minimises expected loss

MinT method (Wickramasuriya, Athanasopoulos, and Hyndman, 2019) minimises

$E [(y y - \tilde{y y})^{'} (y y - \tilde{y y})]$

if $W W$ is set to the inverse forecast error covariance of the base forecasts.

Subject to linearity and constraint that unbiasedness of base forecasts is preserved.

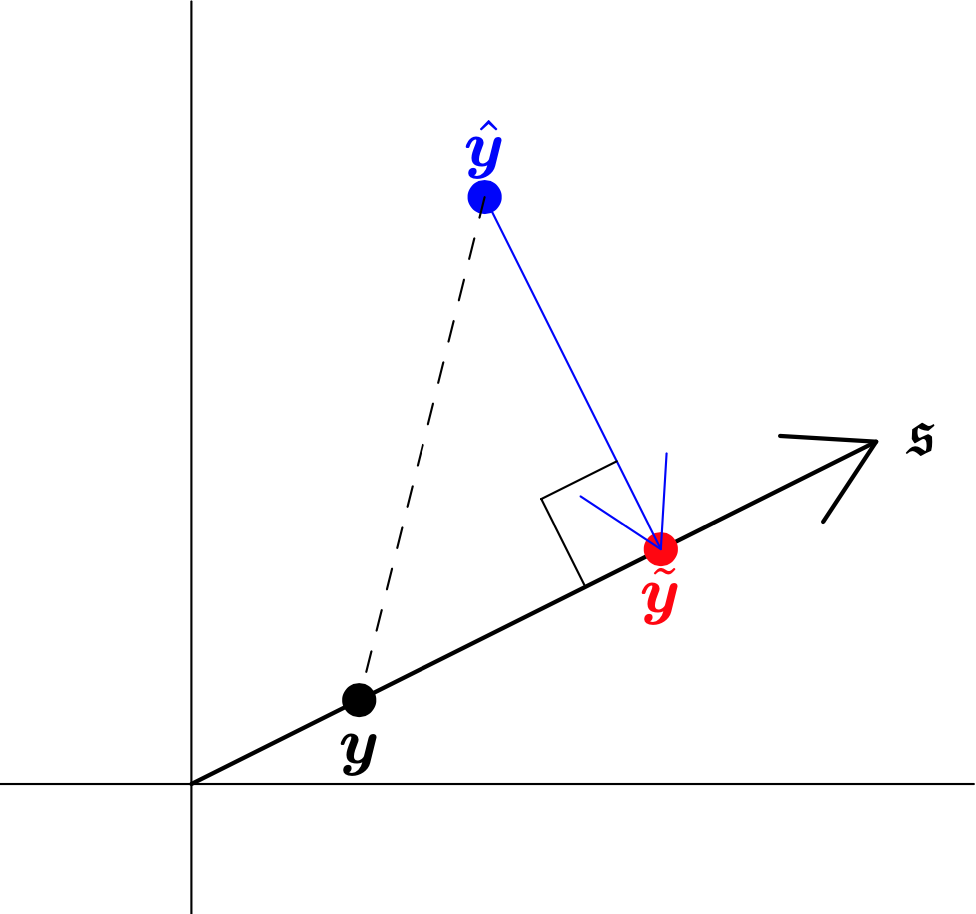
Why optimal? Always improves loss

Reconciliation also minimises

$(\tilde{y y} - \hat{y y})^{'} W W (\tilde{y y} - \hat{y y})$

Subject to $\tilde{y y}$ being coherent.
Guarantee $(y y - \hat{y y})^{'} W W (y y - \hat{y y}) \geq (y y - \tilde{y y})^{'} W W (y y - \tilde{y y})$

With non negativity

For data that cannot be negative can minimise

$(\tilde{y y} - \hat{y y})^{'} W W (\tilde{y y} - \hat{y y})$

Subject to the coherence constraint.
Subject to the constraint that ${\tilde{y}}_{i} \geq 0$ for all $i$ .

With non negativity

For data that cannot be negative can minimise

$(\tilde{y y} - \hat{y y})^{'} W W (\tilde{y y} - \hat{y y})$

Subject to the coherence constraint.
Subject to the constraint that ${\tilde{y}}_{i} \geq 0$ for all $i$ .
Solved by QP using a block pivoting algorithm (Wickramasuriya, Turlach, and Hyndman, 2020).

With non negativity

For data that cannot be negative can minimise

$(\tilde{y y} - \hat{y y})^{'} W W (\tilde{y y} - \hat{y y})$

Subject to the coherence constraint.
Subject to the constraint that ${\tilde{y}}_{i} \geq 0$ for all $i$ .
Solved by QP using a block pivoting algorithm (Wickramasuriya, Turlach, and Hyndman, 2020).
Theory does not follow through, but useful in practice.

Motivation12

Joint loss functionEverything we know about why reconciliation works applies to a joint loss function.
13

Joint loss functionEverything we know about why reconciliation works applies to a joint loss function.
Forecast accuracy for individual variables may become worse after reconciling.
13

Joint loss functionEverything we know about why reconciliation works applies to a joint loss function.
Forecast accuracy for individual variables may become worse after reconciling.
13

Unbiased top down

For 3-variable hierarchy $y_{T} = y_{A} + y_{B}$ , consider

$(\begin{matrix} {\hat{y}}_{T} \\ {\hat{y}}_{A} \\ {\hat{y}}_{T} - {\hat{y}}_{A} \end{matrix}) or (\begin{matrix} {\hat{y}}_{T} \\ {\hat{y}}_{T} - {\hat{y}}_{B} \\ {\hat{y}}_{B} \end{matrix})$

or an average of these (Hollyman, Petropoulos, and Tipping, 2021).

Top level remains unchanged (or immutable) and unbiasedness is preserved

Our contributionSuppose we want to keep forecasts of a subset of variables immutable.
15

Our contributionSuppose we want to keep forecasts of a subset of variables immutable.  When is this feasible?
How should we choose immutable series?

15

Our contributionSuppose we want to keep forecasts of a subset of variables immutable.  When is this feasible?
How should we choose immutable series?

We provide a conclusive answer to the first question and some suggestions (with an empirical example) for the second.
15

Is it feasible?16

Feasbility checkCannot keep Region 1, Store 1A and Store 1B immutable
17

Basis seriesChoose any representation yy=SSbbyy=SSbb.
18

Basis seriesChoose any representation yy=SSbbyy=SSbb.
Let j1,j2,…,jmj1,j2,…,jm be the indices of a set of proposed immutable series
18

Basis seriesChoose any representation yy=SSbbyy=SSbb.
Let j1,j2,…,jmj1,j2,…,jm be the indices of a set of proposed immutable series
Construct a matrix SS{j}SS{j} using the rows of SSSS corresponding to the indices j1,j2,…,jmj1,j2,…,jm.
18

Basis seriesChoose any representation yy=SSbbyy=SSbb.
Let j1,j2,…,jmj1,j2,…,jm be the indices of a set of proposed immutable series
Construct a matrix SS{j}SS{j} using the rows of SSSS corresponding to the indices j1,j2,…,jmj1,j2,…,jm.
If SS{j}SS{j} has full (row) rank, then yj1,yj2,…,yjmyj1,yj2,…,yjm can be kept immutable.
18

Example

$S = (\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$

Example

$S = (\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix})$

Reconciliation

Find $\tilde{y y}$ to minimise

$(\tilde{y y} - \hat{y y})^{'} W W (\tilde{y y} - \hat{y y})$

subject to

Reconciliation

Find $\tilde{y y}$ to minimise

$(\tilde{y y} - \hat{y y})^{'} W W (\tilde{y y} - \hat{y y})$

subject to

Coherence constraints
Immutability constraints
Non negativity constraints

Choosing immutable series22

ApplicationSales data from Chinese online retailer
23

ApplicationSales data from Chinese online retailerConsider "Food" sales as top level.
There are 40 "middle" level categories.
There are 1905 "bottom" level categories.

23

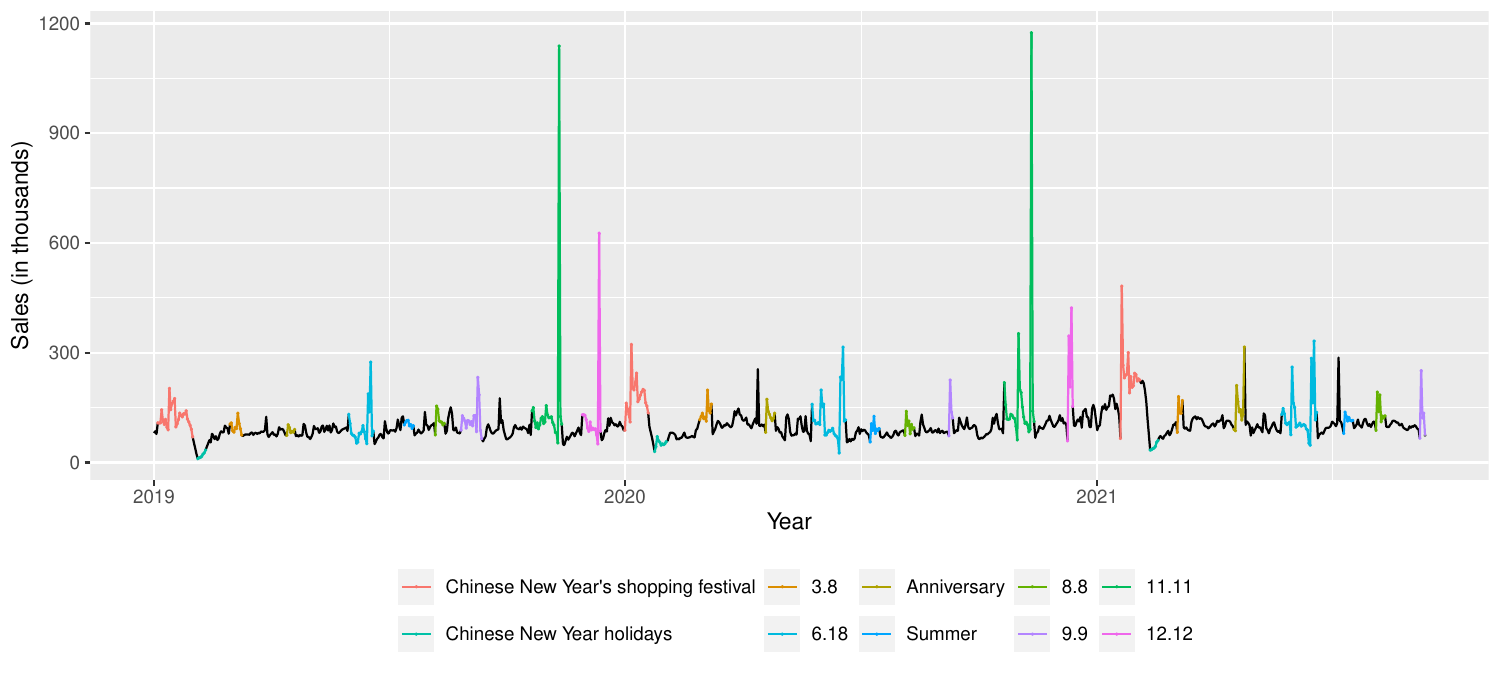
ApplicationSales data from Chinese online retailerConsider "Food" sales as top level.
There are 40 "middle" level categories.
There are 1905 "bottom" level categories.

Many series are intermittent.
Promotions are very important
23

Top level

SetupBase models
25

SetupBase modelsIntermittent Series (more than 60% zeroes) use simple exponential smoothing.
Regression (predictors are strength of promotion) with ARIMA errors and Box Cox transformation for other series.

25

SetupBase modelsIntermittent Series (more than 60% zeroes) use simple exponential smoothing.
Regression (predictors are strength of promotion) with ARIMA errors and Box Cox transformation for other series.

Immutable series
25

SetupBase modelsIntermittent Series (more than 60% zeroes) use simple exponential smoothing.
Regression (predictors are strength of promotion) with ARIMA errors and Box Cox transformation for other series.

Immutable seriesTop level
Series with longer histories (more than 1 year) 

25

Results
 
    Level 
    Base 
    C 
    CN 
    CI 
    CIN 
  


    Top (I) 
    2.94 
    2.75 
    2.77 
    2.94 
    2.94 
  

    Middle (M) 
    2.66 
    2.39 
    2.40 
    2.43 
    2.47 
  

    Bottom (M) 
    2.04 
    1.86 
    1.83 
    1.97 
    1.88 
  

    Intermittent (I) 
    0.11 
    1.52 
    1.52 
    0.11 
    0.11 
  

    Older (I) 
    1.08 
    1.58 
    1.19 
    1.08 
    1.08 
  

26

Level	Base	C	CN	CI	CIN
Top (I)	2.94	2.75	2.77	2.94	2.94
Middle (M)	2.66	2.39	2.40	2.43	2.47
Bottom (M)	2.04	1.86	1.83	1.97	1.88
Intermittent (I)	0.11	1.52	1.52	0.11	0.11
Older (I)	1.08	1.58	1.19	1.08	1.08

ConclusionsImposing immutability constraints still leads to improvements over base forecasts.
27

ConclusionsImposing immutability constraints still leads to improvements over base forecasts.
Immutability stabilises forecasting performance of intermittent series in particular.
27

ConclusionsImposing immutability constraints still leads to improvements over base forecasts.
Immutability stabilises forecasting performance of intermittent series in particular.
Imposing immutability does not lead to better accuracy in all series.
27

ConclusionsImposing immutability constraints still leads to improvements over base forecasts.
Immutability stabilises forecasting performance of intermittent series in particular.
Imposing immutability does not lead to better accuracy in all series.
Imposing non-negativity constraints generally improves performance.
27

Open QuestionsCan we choose immutability constraints in a more principled way?
28

Open QuestionsCan we choose immutability constraints in a more principled way?
Is this another version of a shrinkage v sparsity question?
28

Open QuestionsCan we choose immutability constraints in a more principled way?
Is this another version of a shrinkage v sparsity question?
When is it possible reconcile in a way that yields Pareto improvements in forecast accuracy?
28

References

Gross, C. W. et al. (1990). "Disaggregation methods to expedite product line forecasting". In: Journal of Forecasting 9.3, pp. 233-254.

Hollyman, R. et al. (2021). "Understanding Forecast Reconciliation". En. In: European Journal of Operational Research 294.1, pp. 149-160. ISSN: 0377-2217. DOI: 10.1016/j.ejor.2021.01.017.

Hyndman, R. J. et al. (2011). "Optimal Combination Forecasts for Hierarchical Time Series". En. In: Computational Statistics Data Analysis 55.9, pp. 2579-2589. ISSN: 0167-9473. DOI: 10.1016/j.csda.2011.03.006.

Schwarzkopf, A. B. et al. (1988). "Top-down versus bottom-up forecasting strategies". In: International Journal of Production Research 26 (11), pp. 1833-1843.

Wickramasuriya, S. L. et al. (2019). "Optimal Forecast Reconciliation for Hierarchical and Grouped Time Series Through Trace Minimization". In: Journal of the American Statistical Association 114.526, pp. 804-819. ISSN: 0162-1459. DOI: 10.1080/01621459.2018.1448825.

Wickramasuriya, S. L. et al. (2020). "Optimal Non-Negative Forecast Reconciliation". En. In: Statistics and Computing 30.5, pp. 1167-1182. ISSN: 1573-1375. DOI: 10.1007/s11222-020-09930-0.

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Reconciliation with Immutable Forecasts

Anastasios Panagiotelis

December 1, 2022

Joint work with

Joint work with

Joint work with

Reconciliation background

Hierarchical Time Series

Hierarchical Time Series

Hierarchical Time Series

Problem context

Problem context

Problem context

Problem context

Problem context

Reconciliation

Reconciliation

Reconciliation

Reconciliation

What is SSSS?

What is SSSS?

Why optimal? Minimises expected loss

Why optimal? Minimises expected loss

Why optimal? Always improves loss

With non negativity

With non negativity

With non negativity

Motivation

Joint loss function

Joint loss function

Joint loss function

Unbiased top down

Our contribution

Our contribution

Our contribution

Is it feasible?

Feasbility check

Basis series

Basis series

Basis series

Basis series

Example

Example

Reconciliation

Reconciliation

Choosing immutable series

Application

Application

Application

Top level

Setup

Setup

Setup

Setup

Results

Conclusions

Conclusions

Conclusions

Conclusions

Open Questions

Open Questions

Open Questions

References

Joint work with

Help

Reconciliation
with Immutable
Forecasts

What is $S S$ ?

What is $S S$ ?