Probabilistic
Forecast
Reconciliation
Properties, Evaluation
and Score Optimisation
Anastasios Panagiotelis
September 23, 2020
Joint work with
Puwasala Gamakumara 
Joint work with
Puwasala Gamakumara 
George Athanasopoulos 
Joint work with
Puwasala Gamakumara 
George Athanasopoulos 
Rob Hyndman 
Motivation
Hierarchical Time Series
- Predictions of multiple variables needed.
Hierarchical Time Series
- Predictions of multiple variables needed.
- Variables follow linear constraints.
Hierarchical Time Series
- Predictions of multiple variables needed.
- Variables follow linear constraints.
- Forecast store level sales and aggregates.
Electricity Example
- Total daily electricity in Australian NEM
Electricity Example
- Total daily electricity in Australian NEM
- Renewable
- Non-renewable
Electricity Example
- Total daily electricity in Australian NEM
- Renewable
- Non-renewable
- Renewable can be broken down
Electricity Example
- Total daily electricity in Australian NEM
- Renewable
- Non-renewable
- Renewable can be broken down
- Solar
- Wind
- etc.
Electricity Example
- Total daily electricity in Australian NEM
- Renewable
- Non-renewable
- Renewable can be broken down
- Solar
- Wind
- etc.
- Solar can be broken down into
Electricity Example
- Total daily electricity in Australian NEM
- Renewable
- Non-renewable
- Renewable can be broken down
- Solar
- Wind
- etc.
- Solar can be broken down into
- Solar rooftop
- Solar utility
Electricity Example
- Total daily electricity in Australian NEM
- Renewable
- Non-renewable
- Renewable can be broken down
- Solar
- Wind
- etc.
- Solar can be broken down into
- Solar rooftop
- Solar utility
- Data sourced from Open NEM.
Electricity Data (link)
Main takeaways
- Data have different characteristics regarding
Main takeaways
- Data have different characteristics regarding
- Trends
- Seasonality
- Spikes
- Signal to noise ratio
Main takeaways
- Data have different characteristics regarding
- Trends
- Seasonality
- Spikes
- Signal to noise ratio
- Hard to come up with a single multivariate model.
Main takeaways
- Data have different characteristics regarding
- Trends
- Seasonality
- Spikes
- Signal to noise ratio
- Hard to come up with a single multivariate model.
- Even harder to do so while accounting for constraints.
Why multivariate?
- Electricity cannot be economically stored at large scale (yet).
Why multivariate?
- Electricity cannot be economically stored at large scale (yet).
- Day ahead load forecasting crucial input to dispatch and operational decisions.
Why multivariate?
- Electricity cannot be economically stored at large scale (yet).
- Day ahead load forecasting crucial input to dispatch and operational decisions.
- Increased use of renewables result in uncertainty in supply.
Why multivariate?
- Electricity cannot be economically stored at large scale (yet).
- Day ahead load forecasting crucial input to dispatch and operational decisions.
- Increased use of renewables result in uncertainty in supply.
- Decisions of generators, market regulators may depend on total generation but also on generation from individual sources.
Why multivariate?
- Electricity cannot be economically stored at large scale (yet).
- Day ahead load forecasting crucial input to dispatch and operational decisions.
- Increased use of renewables result in uncertainty in supply.
- Decisions of generators, market regulators may depend on total generation but also on generation from individual sources.
- Avoid non-aligned decisions.
Why probabilistic?
- Prices are heavily right skewed.
Why probabilistic?
- Prices are heavily right skewed.
- Prices in NSW reached $14700 on January 4th,2020.
- This compares to $30-$40 on a normal day.
Why probabilistic?
- Prices are heavily right skewed.
- Prices in NSW reached $14700 on January 4th,2020.
- This compares to $30-$40 on a normal day.
- Price peaks coincide with the use of fuels with higher marginal cost.
Why probabilistic?
- Prices are heavily right skewed.
- Prices in NSW reached $14700 on January 4th,2020.
- This compares to $30-$40 on a normal day.
- Price peaks coincide with the use of fuels with higher marginal cost.
- Another important consideration is grid reliability.
Why probabilistic?
- Prices are heavily right skewed.
- Prices in NSW reached $14700 on January 4th,2020.
- This compares to $30-$40 on a normal day.
- Price peaks coincide with the use of fuels with higher marginal cost.
- Another important consideration is grid reliability.
- Tails are important!
What is reconciliation?
Traditional approaches
- Single level approaches
Traditional approaches
- Single level approaches
- Bottom Up (Schwarzkopf, Tersine, and Morris, 1988).
Traditional approaches
- Single level approaches
- Bottom Up (Schwarzkopf, Tersine, and Morris, 1988).
- Top Down (Gross and Sohl, 1990).
Traditional approaches
- Single level approaches
- Bottom Up (Schwarzkopf, Tersine, and Morris, 1988).
- Top Down (Gross and Sohl, 1990).
- Middle Out
Traditional approaches
- Single level approaches
- Bottom Up (Schwarzkopf, Tersine, and Morris, 1988).
- Top Down (Gross and Sohl, 1990).
- Middle Out
- Top down do not exploit information at bottom levels.
Traditional approaches
- Single level approaches
- Bottom Up (Schwarzkopf, Tersine, and Morris, 1988).
- Top Down (Gross and Sohl, 1990).
- Middle Out
- Top down do not exploit information at bottom levels.
- Bottom up can suffer from the noisiness of bottom level series.
Traditional approaches
- Single level approaches
- Bottom Up (Schwarzkopf, Tersine, and Morris, 1988).
- Top Down (Gross and Sohl, 1990).
- Middle Out
- Top down do not exploit information at bottom levels.
- Bottom up can suffer from the noisiness of bottom level series.
- These approaches do not work for more general constraints.
Reconciliation
- Forecast every variable, stack in an n-vector ^y.
- Call these base forecasts.
- Forecasts not coherent.
- Forecasts need to be reconciled via a mapping ~y=ψ(^y).
Reconciliation
- Forecast every variable, stack in an n-vector ^y.
- Call these base forecasts.
- Forecasts not coherent.
- Forecasts need to be reconciled via a mapping ~y=ψ(^y).
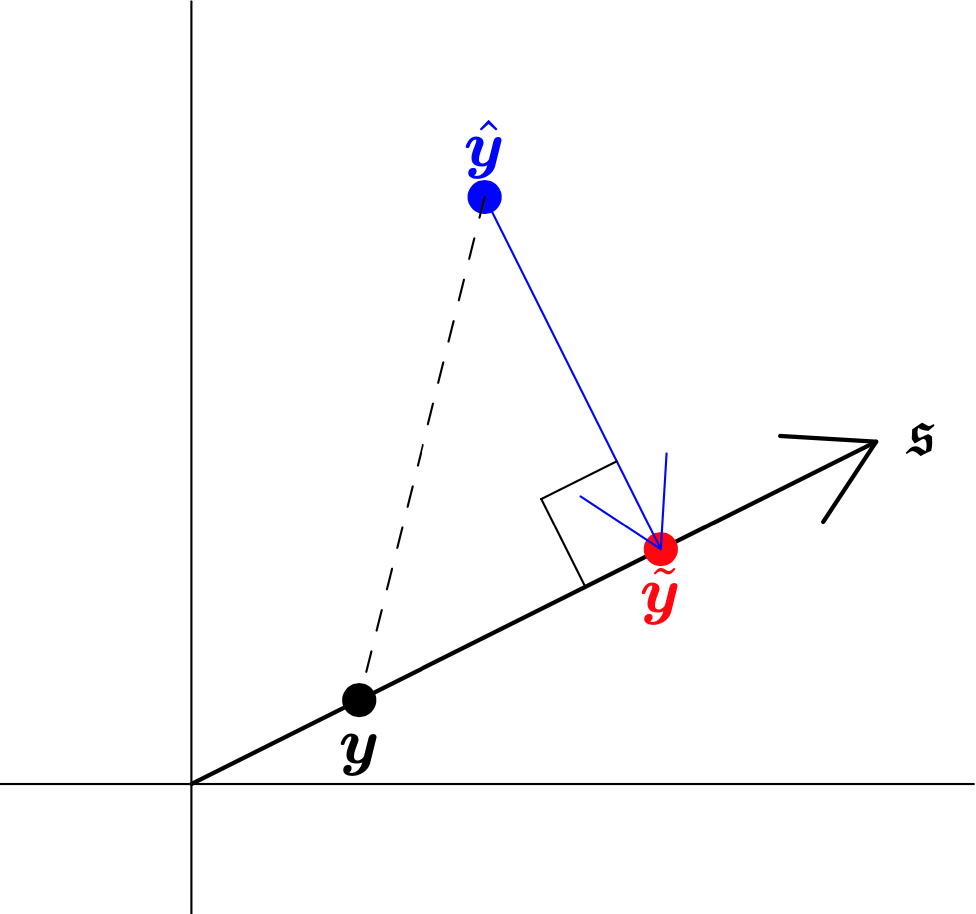
Some math
Linear reconciliation generally takes the form ~b=(d+G^y) where
Some math
Linear reconciliation generally takes the form ~b=(d+G^y) where
- G is an m×n matrix of reconciliation weights
- d is m×1 translation vector
Some math
Linear reconciliation generally takes the form ~b=(d+G^y) where
- G is an m×n matrix of reconciliation weights
- d is m×1 translation vector
The full hierarchy is ~y=S~b where S is an n×m matrix that encodes constraints.
The summing matrix
The summing matrix
S=⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝1111110000111000010000100001⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠
Specific reconciliation methods
- OLS: ~y=S(S′S)−1S′^y
- Hyndman, Ahmed, Athanasopoulos, and Shang (2011)
Specific reconciliation methods
- OLS: ~y=S(S′S)−1S′^y
- Hyndman, Ahmed, Athanasopoulos, and Shang (2011)
- WLS: ~y=S(S′WS)−1S′W^y
- Athanasopoulos, Hyndman, Kourentzes, and Petropoulos (2017)
Specific reconciliation methods
- OLS: ~y=S(S′S)−1S′^y
- Hyndman, Ahmed, Athanasopoulos, and Shang (2011)
- WLS: ~y=S(S′WS)−1S′W^y
- Athanasopoulos, Hyndman, Kourentzes, and Petropoulos (2017)
- MinT: ~y=S(S′Σ−1S)−1S′Σ−1^y
- Wickramasuriya, Athanasopoulos, and Hyndman (2019)
Probabilistic forecasts
Existing approaches
- Stack quantiles of each series in a vector and reconcile
- Shang and Hyndman (2017) for prediction intervals.
- Jeon, Panagiotelis, and Petropoulos (2019) (hereafter JPP) for a full distribution.
Existing approaches
- Stack quantiles of each series in a vector and reconcile
- Shang and Hyndman (2017) for prediction intervals.
- Jeon, Panagiotelis, and Petropoulos (2019) (hereafter JPP) for a full distribution.
- Reconcile mean otherwise bottom up
- Ben Taieb, Taylor, and Hyndman (2020) (hereafter BTTH)
Formal Definition: Coherence
- Let (Rm,FRm,μ) be a probability triple
- Let s:Rm→s where s(.) is premultiplication by S.
Formal Definition: Coherence
- Let (Rm,FRm,μ) be a probability triple
- Let s:Rm→s where s(.) is premultiplication by S.
- A coherent probabilistic forecast can be characterised by a probability triple (s,Fs,ν) where
ν(s(B))=μ(B)∀B∈FRm and s(B) is the image of B under s(.).
In a picture
Formal Definition: Reconciliation
Let (Rn,FRn,^ν) be a probability triple corresponding to a base forecast.
Formal Definition: Reconciliation
Let (Rn,FRn,^ν) be a probability triple corresponding to a base forecast.
The reconcilied forecast is characterised by
~ν(A)=^ν(ψ−1(A))∀A∈Fs and ψ−1(A) is the pre-image of A under ψ(.).
In a picture
In practice
If ^y[1],…,^y[L] is a sample from some base probabilistic forecast, then ~y[1],…,~y[L] is a sample from the reconciled forecast where
~y[l]=ψ(^y[l])∀l=1,…,L
In practice
If ^y[1],…,^y[L] is a sample from some base probabilistic forecast, then ~y[1],…,~y[L] is a sample from the reconciled forecast where
~y[l]=ψ(^y[l])∀l=1,…,L Reconciling a sample from the base distribution gives a sample from the reconciled distribution.
In practice
If ^y[1],…,^y[L] is a sample from some base probabilistic forecast, then ~y[1],…,~y[L] is a sample from the reconciled forecast where
~y[l]=ψ(^y[l])∀l=1,…,L Reconciling a sample from the base distribution gives a sample from the reconciled distribution.
Proof in paper.
In practice
- If the base forecast is elliptical, then the reconcilied forecast will be elliptical.
In practice
- If the base forecast is elliptical, then the reconcilied forecast will be elliptical.
- If the base forecast is N(^μ,^Σ)
In practice
- If the base forecast is elliptical, then the reconcilied forecast will be elliptical.
- If the base forecast is N(^μ,^Σ)
- If reconciliation is linear ψ(^y):=S(d+G^y)
In practice
- If the base forecast is elliptical, then the reconcilied forecast will be elliptical.
- If the base forecast is N(^μ,^Σ)
- If reconciliation is linear ψ(^y):=S(d+G^y)
- The reconciled forecast is N(S(d+G^μ),SG^ΣG′S′)
Perfect Reconciliation
- Using the result on the previous slide we prove that for an arbitrary ^μ and ^Σ there exists a d and G that recovers the true predictive distribution.
Perfect Reconciliation
- Using the result on the previous slide we prove that for an arbitrary ^μ and ^Σ there exists a d and G that recovers the true predictive distribution.
- No matter how bad the base forecast is reconciliation can get you to the truth.
Perfect Reconciliation
- Using the result on the previous slide we prove that for an arbitrary ^μ and ^Σ there exists a d and G that recovers the true predictive distribution.
- No matter how bad the base forecast is reconciliation can get you to the truth.
- It is not feasible.
Perfect Reconciliation
- Using the result on the previous slide we prove that for an arbitrary ^μ and ^Σ there exists a d and G that recovers the true predictive distribution.
- No matter how bad the base forecast is reconciliation can get you to the truth.
- It is not feasible.
- Will not always be a projection.
Score Optimisation
Scoring Rules
- Propose reconciliation by optimising with respect to a scoring rule (Gneiting and Raftery, 2007).
Scoring Rules
- Propose reconciliation by optimising with respect to a scoring rule (Gneiting and Raftery, 2007).
- A scoring rule K(q,ω) takes a probabilistic forecast q and a realisation ω and returns a real number.
Scoring Rules
- Propose reconciliation by optimising with respect to a scoring rule (Gneiting and Raftery, 2007).
- A scoring rule K(q,ω) takes a probabilistic forecast q and a realisation ω and returns a real number.
- The rule is proper if
Ep[K(p,ω)]≤Ep[K(q,ω)]
for all p≠q where ω∼p
Multivariate scoring rules
- Log score
Multivariate scoring rules
- Log score
- Improper in context of reconciliation.
- Result proven in paper.
Multivariate scoring rules
- Log score
- Improper in context of reconciliation.
- Result proven in paper.
- Energy score
Multivariate scoring rules
- Log score
- Improper in context of reconciliation.
- Result proven in paper.
- Energy score
- Multivariate generalisation of continuous ranked probability score.
Multivariate scoring rules
- Log score
- Improper in context of reconciliation.
- Result proven in paper.
- Energy score
- Multivariate generalisation of continuous ranked probability score.
- Variogram score (Scheuerer and Hamill, 2015)
If d and G known
Use training data t=1,…,T to train models and make base forecasts.
If d and G known
Use training data t=1,…,T to train models and make base forecasts.
Then reconcile.
Training d and G
In math
Optimise E(γ)=T+R−1∑t=TK(~fγt+h|t,yt+h)
In math
Optimise E(γ)=T+R−1∑t=TK(~fγt+h|t,yt+h) where ~fγt+h|t is reconciled with respect to γ:=(d,vec(G))
In math
Optimise E(γ)=T+R−1∑t=TK(~fγt+h|t,yt+h) where ~fγt+h|t is reconciled with respect to γ:=(d,vec(G))
- Energy and variogram score approximated via Monte Carlo.
Energy Score
E(γ)≈T+R−1∑t=T[1Q(Q∑q=1||~y[q]t+h|t−yt+h||−12||~y[q]t+h|t−~y∗[q]t+h|t||)]
Energy Score
E(γ)≈T+R−1∑t=T[1Q(Q∑q=1||~y[q]t+h|t−yt+h||−12||~y[q]t+h|t−~y∗[q]t+h|t||)] ~y[q]t+h|t=S(d+G^y[q]t+h|t), ~y∗[q]t+h|t=S(d+G^y∗[q]t+h|t) and ^y[q]t+h|t,^y∗[q]t+h|tiid∼^ft+h|t for q=1,…,Q
Stochastic Gradient Descent
- When the objective function is only known up to approximation Stochastic Gradient Descent can be used for optimisation.
Stochastic Gradient Descent
- When the objective function is only known up to approximation Stochastic Gradient Descent can be used for optimisation.
- Requires an estimate of the gradient found by Automatic Differentiation.
Stochastic Gradient Descent
- When the objective function is only known up to approximation Stochastic Gradient Descent can be used for optimisation.
- Requires an estimate of the gradient found by Automatic Differentiation.
- The specific variant of SGD used is Adam (Kingma and Ba, 2014).
Stochastic Gradient Descent
- When the objective function is only known up to approximation Stochastic Gradient Descent can be used for optimisation.
- Requires an estimate of the gradient found by Automatic Differentiation.
- The specific variant of SGD used is Adam (Kingma and Ba, 2014).
- Implementation available in ProbReco package.
Simulation
Scenarios
Simulate from 7-variable hierarchy with bottom levels given by ARIMA models
Scenarios
Simulate from 7-variable hierarchy with bottom levels given by ARIMA models
- Stationary Gaussian
Scenarios
Simulate from 7-variable hierarchy with bottom levels given by ARIMA models
- Stationary Gaussian
- Stationary non-Gaussian
Scenarios
Simulate from 7-variable hierarchy with bottom levels given by ARIMA models
- Stationary Gaussian
- Stationary non-Gaussian
- Non-stationary Gaussian
Scenarios
Simulate from 7-variable hierarchy with bottom levels given by ARIMA models
- Stationary Gaussian
- Stationary non-Gaussian
- Non-stationary Gaussian
- Non-stationary non-Gaussian
Base forecasts
Obtain point forecasts from ARIMA or ETS models. To sample from base probabilistic forecasts add noise that is
Base forecasts
Obtain point forecasts from ARIMA or ETS models. To sample from base probabilistic forecasts add noise that is
- Independent Gaussian noise
Base forecasts
Obtain point forecasts from ARIMA or ETS models. To sample from base probabilistic forecasts add noise that is
- Independent Gaussian noise
- Multivariate Gaussian noise
Base forecasts
Obtain point forecasts from ARIMA or ETS models. To sample from base probabilistic forecasts add noise that is
- Independent Gaussian noise
- Multivariate Gaussian noise
- Bootstraped residuals
Base forecasts
Obtain point forecasts from ARIMA or ETS models. To sample from base probabilistic forecasts add noise that is
- Independent Gaussian noise
- Multivariate Gaussian noise
- Bootstraped residuals
- Jointly bootstapped residuals
Residual Matrix
⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝eTot,1⋯eTot,t⋯eTot,TeA,1⋯eA,t⋯eA,TeB,1⋯eB,t⋯eB,TeAA,1⋯eAA,t⋯eAA,TeAB,1⋯eAB,t⋯eAB,TeBA,1⋯eBA,t⋯eBA,TeBB,1⋯eBB,t⋯eBB,T⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠
Independently Bootstapped
⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝eTot,1⋯eTot,t⋯eTot,TeA,1⋯eA,t⋯eA,TeB,1⋯eB,t⋯eB,TeAA,1⋯eAA,t⋯eAA,TeAB,1⋯eAB,t⋯eAB,TeBA,1⋯eBA,t⋯eBA,TeBB,1⋯eBB,t⋯eBB,T⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠
Jointly Bootstapped
⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝eTot,1⋯eTot,t⋯eTot,TeA,1⋯eA,t⋯eA,TeB,1⋯eB,t⋯eB,TeAA,1⋯eAA,t⋯eAA,TeAB,1⋯eAB,t⋯eAB,TeBA,1⋯eBA,t⋯eBA,TeBB,1⋯eBB,t⋯eBB,T⎞⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟⎠
Reconciliation methods
- JPP: Reconcile quantiles.
Reconciliation methods
- JPP: Reconcile quantiles.
- BTTH: Reconcile mean, otherwise BU.
Reconciliation methods
- JPP: Reconcile quantiles.
- BTTH: Reconcile mean, otherwise BU.
- BU: Bottom up.
Reconciliation methods
- JPP: Reconcile quantiles.
- BTTH: Reconcile mean, otherwise BU.
- BU: Bottom up.
- OLS: Orthogonal projection.
Reconciliation methods
- JPP: Reconcile quantiles.
- BTTH: Reconcile mean, otherwise BU.
- BU: Bottom up.
- OLS: Orthogonal projection.
- MinT: With shrinkage estimator.
Reconciliation methods
- JPP: Reconcile quantiles.
- BTTH: Reconcile mean, otherwise BU.
- BU: Bottom up.
- OLS: Orthogonal projection.
- MinT: With shrinkage estimator.
- ScoreOptE: Optimise w.r.t Energy Score.
Reconciliation methods
- JPP: Reconcile quantiles.
- BTTH: Reconcile mean, otherwise BU.
- BU: Bottom up.
- OLS: Orthogonal projection.
- MinT: With shrinkage estimator.
- ScoreOptE: Optimise w.r.t Energy Score.
- ScoreOptV: Optimise w.r.t Variogram Score.
Simulation Results (link)
Energy application
Base forecasts
Use a feed-forward neural network with up to 28 lags of daily data. For probabilisitic forecasts:
Base forecasts
Use a feed-forward neural network with up to 28 lags of daily data. For probabilisitic forecasts:
- Independent Gaussian noise
Base forecasts
Use a feed-forward neural network with up to 28 lags of daily data. For probabilisitic forecasts:
- Independent Gaussian noise
- Multivariate Gaussian noise
Base forecasts
Use a feed-forward neural network with up to 28 lags of daily data. For probabilisitic forecasts:
- Independent Gaussian noise
- Multivariate Gaussian noise
- Bootstraped residuals
Base forecasts
Use a feed-forward neural network with up to 28 lags of daily data. For probabilisitic forecasts:
- Independent Gaussian noise
- Multivariate Gaussian noise
- Bootstraped residuals
- Jointly bootstapped residuals
Base forecasts
Use a feed-forward neural network with up to 28 lags of daily data. For probabilisitic forecasts:
- Independent Gaussian noise
- Multivariate Gaussian noise
- Bootstraped residuals
- Jointly bootstapped residuals
Consider day-ahead forecasts.
Model Fit (link)
Residual Dependence
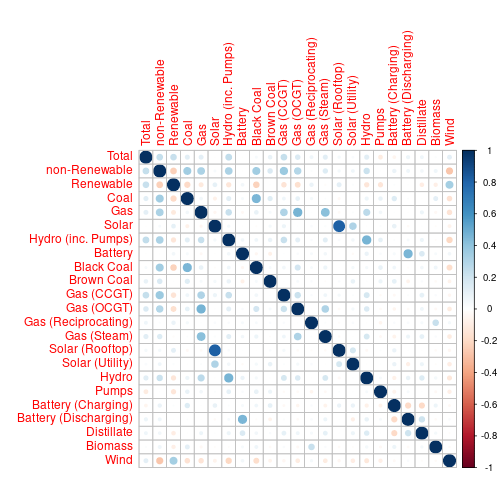
Reconciliation Results
Independent Gaussian
Joint Bootstrap
Main takeaway
- Score optimisation dominates alternatives when base forecasts are badly mis-specified.
Main takeaway
- Score optimisation dominates alternatives when base forecasts are badly mis-specified.
- If base models are good then OLS dominates.
Main takeaway
- Score optimisation dominates alternatives when base forecasts are badly mis-specified.
- If base models are good then OLS dominates.
- Existing approaches in the literature do not work well and are even dominated by base forecasts.
Main takeaway
- Score optimisation dominates alternatives when base forecasts are badly mis-specified.
- If base models are good then OLS dominates.
- Existing approaches in the literature do not work well and are even dominated by base forecasts.
- Possible bias-variance tradeoff at play. Future work may look at regularised approaches to score optimisation.
References
Athanasopoulos, G. et al. (2017). "Forecasting with temporal hierarchies". In: European Journal of Operational Research 262.1, pp. 60-74.
Ben Taieb, S. et al. (2020). "Hierarchical Probabilistic Forecasting of Electricity Demand With Smart Meter Data". In: Journal of the American Statistical Association. in press.
Gneiting, T. et al. (2007). "Strictly Proper Scoring Rules, Prediction, and Estimation". In: Journal of the American Statistical Association 102.477, pp. 359-378.
Gross, C. W. et al. (1990). "Disaggregation methods to expedite product line forecasting". In: Journal of Forecasting 9.3, pp. 233-254.
Hyndman, R. J. et al. (2011). "Optimal combination forecasts for hierarchical time series". In: Computational Statistics and Data Analysis 55.9, pp. 2579-2589.
Jeon, J. et al. (2019). "Probabilistic forecast reconciliation with applications to wind power and electric load". In: European Journal of Operational Research 279.2, pp. 364-379.
Kingma, D. P. et al. (2014). "Adam: A method for stochastic optimization". . http://arxiv.org/abs/1412.6980.
Scheuerer, M. et al. (2015). "Variogram-Based Proper Scoring Rules for Probabilistic Forecasts of Multivariate Quantities". In: Monthly Weather Review 143.4, pp. 1321-1334.
Schwarzkopf, A. B. et al. (1988). "Top-down versus bottom-up forecasting strategies". In: International Journal of Production Research 26 (11), pp. 1833-1843.
Shang, H. L. et al. (2017). "Grouped Functional Time Series Forecasting: An Application to Age-Specific Mortality Rates". In: Journal of Computational and Graphical Statistics 26.2, pp. 330-343.
Wickramasuriya, S. L. et al. (2019). "Optimal Forecast Reconciliation for Hierarchical and Grouped Time Series Through Trace Minimization". In: Journal of the American Statistical Association 114.526, pp. 804-819.