Forecast Reconciliation: A Review

class: center, middle, inverse, title-slide

.title[
# Forecast Reconciliation:<br> A Review
]
.author[
### Anastasios Panagiotelis
]
.date[
### 16th August, 2023
]

---

# Joint work with...

.pull-left[
- Rob Hyndman
- George Athanasopoulos
- Nikos Kourentzes
- Puwasala Gamakumara
- Mohamaed Affan
- Han Li
]
.pull-right[
- Hong Li
- Yang Lu
- Florian Eckert
- Fotios Petropoulos
- Jooyoung Jeon
- Bohan Zhang
- Yanfei Kang
- Feng Li
]

---
class: inverse, center, middle

# Motivation

---

# Hierarchical Time Series

- Predictions of multiple variables needed.
--

- Variables follow linear constraints.
--

- Forecast store level sales and aggregates.

<div id="htmlwidget-6cd9f28e9a60e1cd2ba2" style="width:100%;height:300px;" class="widgetframe html-widget"></div>
<script type="application/json" data-for="htmlwidget-6cd9f28e9a60e1cd2ba2">{"x":{"url":"RecoReview_files/figure-html//widgets/widget_unnamed-chunk-1.html","options":{"xdomain":"*","allowfullscreen":false,"lazyload":false}},"evals":[],"jsHooks":[]}</script>

---

# Temporal

<div id="htmlwidget-5a3436086b8d8e7fb33e" style="width:100%;height:300px;" class="widgetframe html-widget"></div>
<script type="application/json" data-for="htmlwidget-5a3436086b8d8e7fb33e">{"x":{"url":"RecoReview_files/figure-html//widgets/widget_unnamed-chunk-2.html","options":{"xdomain":"*","allowfullscreen":false,"lazyload":false}},"evals":[],"jsHooks":[]}</script>

---

# Grouped Time Series

---

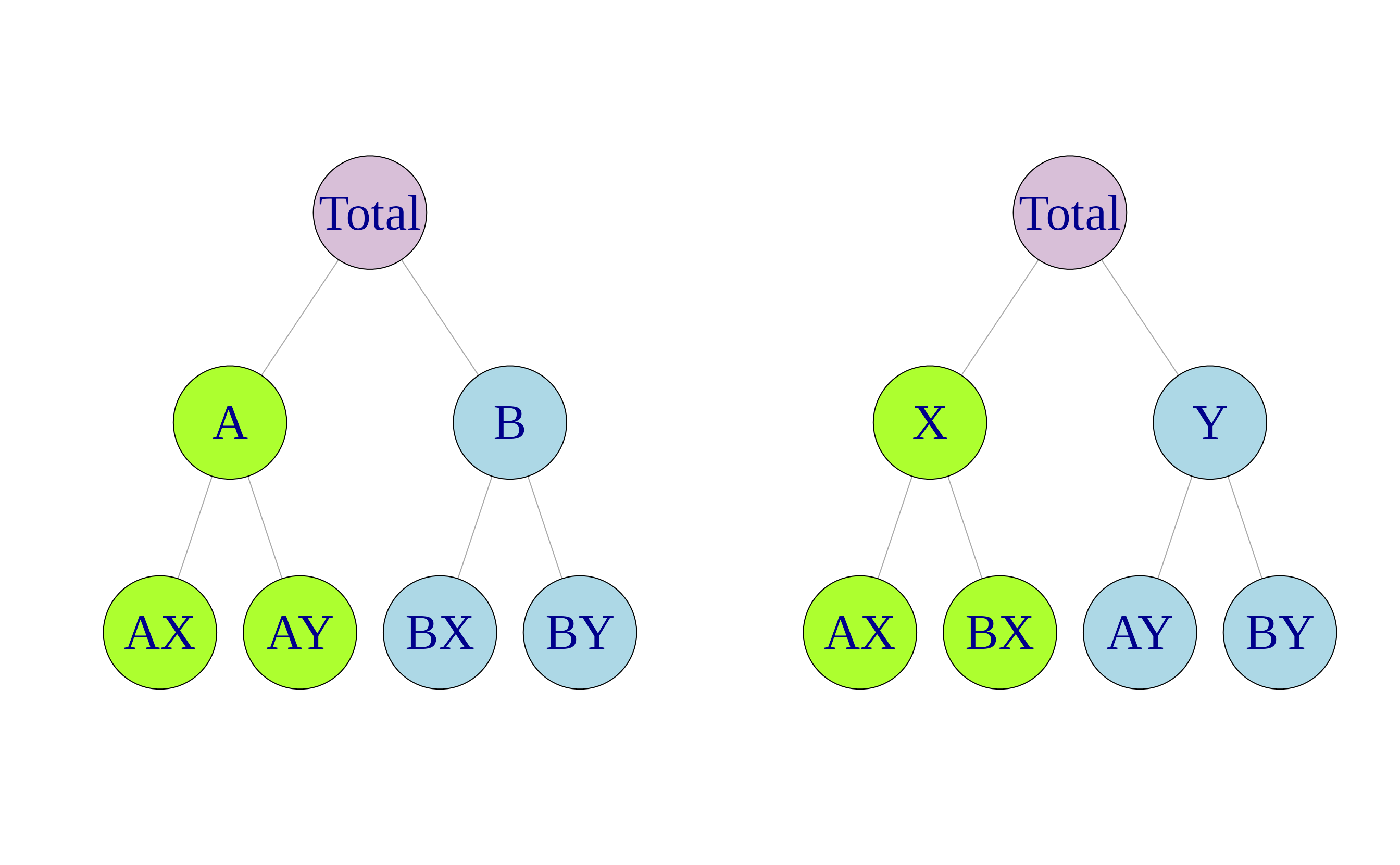
# Examples

- Tourism data grouped by:
  - Region
  - Purpose of travel
- Prison population data grouped by:
  - State
  - Gender

---

# Definition of Hierarchies

- Alternative definitions of 'Hierarchical Time Series':
  - Any collection of `$n$` variables with `$q$` linear constraints.
  - Any collection of `$n$` variables with support on a `$m$`-dimensional linear subspace `$n=m+q$`.
- These are the same. Notably 
  - They do not need to involve aggregation
  - They do not even need to be time series

---

# Electricity Example

- Total daily electricity in Australian NEM
--

- Renewable
  - Non-renewable
--

- Renewable can be broken down 
--

- Solar
  - Wind
  - etc.
--

- Solar can be broken down into
--

- Solar rooftop
  - Solar utility
--

- Data sourced from [Open NEM](opennem.org.au).

---

# Electricity Data [<span style="color:white">(link)</span>](https://anastasiospanagiotelis.shinyapps.io/ProbRecoApp)

---

# Main takeaways

- Data have different characteristics regarding
--
  
  - Trends
  - Seasonality
  - Spikes
  - Signal to noise ratio
--

- Hard to come up with a single multivariate model. 
--

- Even harder to do so while accounting for constraints.

---
class: middle, center, inverse

# What is reconciliation?

---

# Traditional approaches

- Single level approaches
--
  
  - Bottom Up (Schwarzkopf, Tersine, and Morris, 1988).
--
  
  - Top Down (Gross and Sohl, 1990).
--
  
  - Middle Out
--

- Top down do not exploit information at bottom levels.
--

- Bottom up can suffer from the noisiness of bottom level series.
--

- These approaches do not work for more general constraints.

---

# What is reconciliation?

- Traditional approaches only use forecasts at a single level.
--

- **Question:** Why not produce forecasts *for all series*?
--
  
  - **Answer:** They may not respect constraints
--

- **Solution:** Adjust forecasts ex post.
--

- This is called *forecast reconciliation*.

---

# In the beginning

- Some very early examples involving national accounts data
  - Stone, Champernowne, and Meade (1942)
  - Byron (1978)
--

- Literature becomes more focused on forecasting with Hyndman, Ahmed, Athanasopoulos, and Shang (2011)
--

- How did they think about the problem?

---

# The regression interpretation

- Consider the `$n$`-vector of initial (so-called base) forecasts denoted `$\hat{\mathbf{y}}$`.
- Let `$\beta$` be an `$m$`-vector vector of 'true' bottom level forecasts.
- Consider a regression

`$$\hat{\mathbf{y}}=\mathbf{S}\mathbf{\beta}+\epsilon$$`
- What is `$\mathbf{S}$`?

---

# The summing matrix

.pull-left[
<div id="htmlwidget-4af8432f11d33e35e87b" style="width:100%;height:300px;" class="widgetframe html-widget"></div>
<script type="application/json" data-for="htmlwidget-4af8432f11d33e35e87b">{"x":{"url":"RecoReview_files/figure-html//widgets/widget_unnamed-chunk-4.html","options":{"xdomain":"*","allowfullscreen":false,"lazyload":false}},"evals":[],"jsHooks":[]}</script>
]

---

# The summing matrix

.pull-left[
<div id="htmlwidget-2a6f1fa8a6602f9284f8" style="width:100%;height:300px;" class="widgetframe html-widget"></div>
<script type="application/json" data-for="htmlwidget-2a6f1fa8a6602f9284f8">{"x":{"url":"RecoReview_files/figure-html//widgets/widget_unnamed-chunk-5.html","options":{"xdomain":"*","allowfullscreen":false,"lazyload":false}},"evals":[],"jsHooks":[]}</script>
]
.pull-right[
`$\mathbf{S}=\begin{pmatrix}1&1&1&1\\1&1&0&0\\0&0&1&1\\1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}$`
]

---

# The solution

- Can get an 'estimate' of `$\mathbf{\beta}$` via least squares

`$$\hat{\mathbf{\beta}}=\mathbf{(S'S)}^{-1}\mathbf{S'\hat{y}}$$`
--

- Find a full set of coherent forecasts as

`$$\tilde{\mathbf{y}}=\mathbf{S}\mathbf{(S'S)}^{-1}\mathbf{S'\hat{y}}$$`
--

- Here `$\tilde{\mathbf{y}}$` is the *OLS reconciled forecast*.

---

# Other reconciliation methods

- Other reconciliation methods take the form

`$$\tilde{\mathbf{y}}=\mathbf{S}\left(\mathbf{S}'\mathbf{W}\mathbf{S}\right)^{-1}\mathbf{S}'\mathbf{W}\hat{\mathbf{y}}$$` 
- Different choices of `$\mathbf{W}$` 
  - Diagonal (Athanasopoulos, Hyndman, Kourentzes, and Petropoulos, 2017)
  - Error covariance or 'MinT' (Wickramasuriya, Athanasopoulos, and Hyndman, 2019)

---

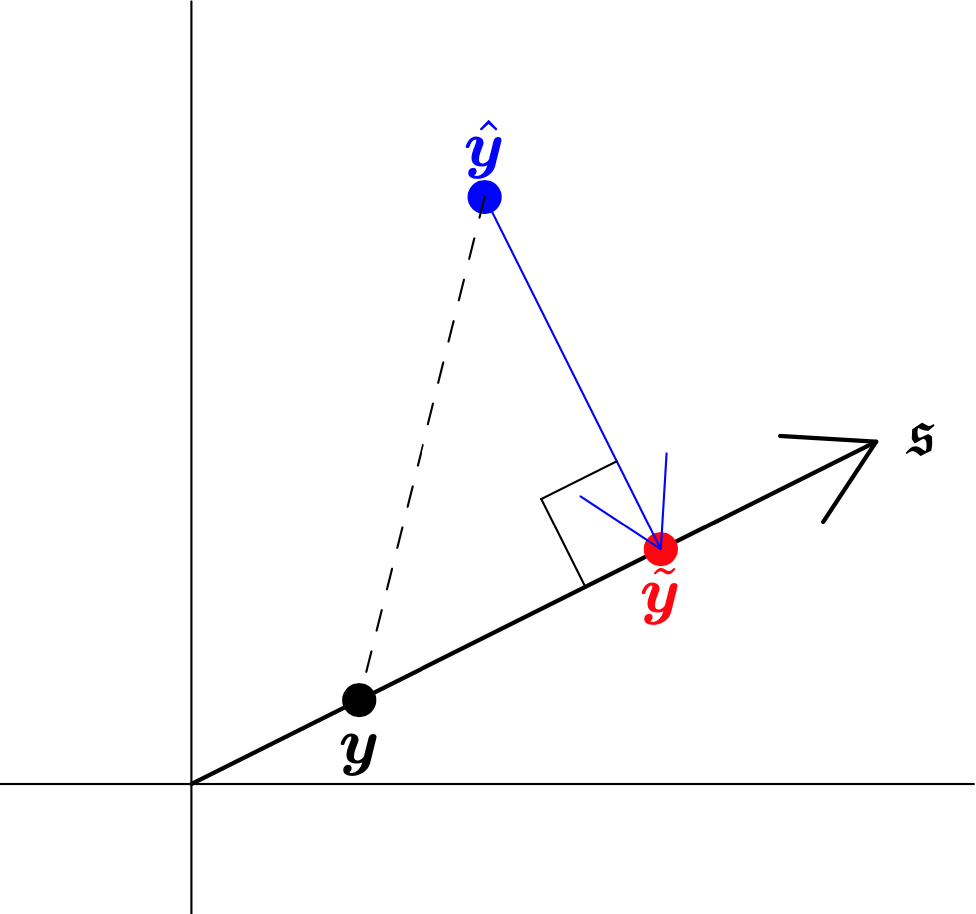
# Geometric Intepretation

.pull-left[
- Base forecasts `$\hat{\mathbf{y}}$` lie somewhere in `$\mathbb{R}^n$`
- Realisation `$\mathbf{y}$` lies on a linear subspace `$\mathfrak{s}$` that is spanned by the columns of `$\mathbf{S}$`.
- Forecasts need to be .emphcol[reconciled] via a mapping `$\tilde{\mathbf{y}}=\psi(\hat{\mathbf{y}})$`.
]

.pull-right[![](img/geo.png)]

---

# Why it works?

- Consider a loss function

`$$L_{\mathbf{W}}(\mathbf{y},\breve{\mathbf{y}})=(\mathbf{y}-\breve{\mathbf{y}})'\mathbf{W}(\mathbf{y}-\breve{\mathbf{y}})$$`
--

- Can prove that for `$\tilde{\mathbf{y}}=\mathbf{S}\left(\mathbf{S}'\mathbf{W}\mathbf{S}\right)^{-1}\mathbf{S}'\mathbf{W}\hat{\mathbf{y}}$`

`$$L_{\mathbf{W}}(\mathbf{y},\tilde{\mathbf{y}})\leq L_{\mathbf{W}}(\mathbf{y},\hat{\mathbf{y}})$$`
- Proof in Panagiotelis, Athanasopoulos, Gamakumara, and Hyndman (2021)

---

#Intuition

---

# Optimality

- Assume unbiased forecasts.
- Can prove that for any `$\mathbf{W}$`, `$E\left[L_{\mathbf{W}}(\mathbf{y},\tilde{\mathbf{y}})\right]$` is minimised by

`$$\tilde{\mathbf{y}}=\mathbf{S}\left(\mathbf{S}'\mathbf{\Sigma}^{-1}\mathbf{S}\right)^{-1}\mathbf{S}'\mathbf{\Sigma}^{-1}\hat{\mathbf{y}}$$`
where `$\mathbf{\Sigma}$` is the forecast error covariance.

`$$\mathbf{\Sigma}=E\left[(\mathbf{y}-\mathbf{\hat{y}})(\mathbf{y}-\mathbf{\hat{y}})'\right]$$`

---

# Intuition

---

# Intuition

---
# Intuition

---
# Intuition

<img src="img/mintint4.svg" width="70%" style="display: block; margin: auto;" />
---

# What theory does not tell us (yet)

- How to reconcile if we are primarily interested in a single series (or subset of series).
--

- How to obtain improvements in forecast accuracy for all series.
--

- How to improve forecast accuracy for losses that are not quadratic.
--

- Nonetheless, the above do often (but not always) hold empirically

---

# Model averaging

- Consider the most simple hierarchy `$T=A+B$`
- There are two forecasts for `$A$`
  - Direct `$\hat{A}$`
  - Indirect `$\hat{T}-\hat{B}$`
- Reconciliation is a model average between the direct and indirect forecasts (Hollyman, Petropoulos, and Tipping, 2021)
--

- Model averaging is a relatively well understood problem.

---

# Other interesting problems

- Discrete reconciliation
  - Zambon, Azzimonti, and Corani (2022)
  - Zhang, Panagiotelis, Li, and Kang (2023)
--

- Cross Temporal Reconciliation
  - Di
Fonzo and Girolimetto (2023)
--

- Machine Learning
  - Spiliotis, Abolghasemi, Hyndman, Petropoulos, and Assimakopoulos (2021)
  - Burba and Chen (2021)

---

class: inverse, middle center

# Probabilistic forecasts

---

# Early attempts

- Reconcile means but otherwise bottom up (Ben Taieb, Taylor, and Hyndman, 2021)
--

- Reconcile quantiles (Jeon, Panagiotelis, and Petropoulos, 2019)
--

- This is only valid under perfectly dependent forecasts
--

- Can notions of coherence and reconciliation be extended to probabilistic setting in a formal way?
- See Panagiotelis, Gamakumara, Athanasopoulos, and Hyndman (2023)

---

# Formal Definition: Coherence

- Let `$\left(\mathbb{R}^m,\mathscr{F}_{\mathbb{R}^m},\mu\right)$` be a probability triple 
- Let `$s:\mathbb{R}^m\rightarrow\mathfrak{s}$` where `$s(.)$` is premultiplication by the matrix `$\mathbf{S}$`.  
--

- Coherent probabilistic forecast characterised by probability triple `$\left(\mathfrak{s},\mathscr{F}_{\mathfrak{s}},\nu\right)$` where

`$$\nu(s(\mathcal{B}))=\mu(\mathcal{B})\quad\forall\mathcal{B}\in{\mathscr{F}_{\mathbb{R}^m}}$$`
and `$s(\mathcal{B})$` is the image of `$\mathcal{B}$` under `$s(.)$`.

---

# In a picture

---

# Formal Definition: Reconciliation

Let `$\left(\mathbb{R}^n,\mathscr{F}_{\mathbb{R}^n},\hat\nu\right)$` be a probability triple corresponding to a base forecast.  
--

The reconciled forecast is characterised by

`$$\tilde\nu(\mathcal{A})=\hat\nu(\psi^{-1}(\mathcal{A}))\quad\forall\mathcal{A}\in\mathscr{F}_{\mathfrak{s}}$$`
and `$\psi^{-1}(\mathcal{A})$` is the pre-image of `$\mathcal{A}$` under `$\psi(.)$`.
--

- The measure `$\tilde{\nu}$` is the *pushforward* of `$\hat{\nu}$`
---

# In a picture

---

# In practice

If `$\hat{\mathbf{y}}^{[1]},\ldots,\hat{\mathbf{y}}^{[L]}$` is a sample from some base probabilistic forecast, then `$\tilde{\mathbf{y}}^{[1]},\ldots,\tilde{\mathbf{y}}^{[L]}$` is a sample from the reconciled forecast where

`$$\tilde{\mathbf{y}}^{[l]}=\psi(\hat{\mathbf{y}}^{[l]})\quad\forall l=1,\ldots,L$$`
--

*Reconciling a sample from the base distribution gives a sample from the reconciled distribution.*
--

---

# Some results

- For elliptical distributions linear reconciliation leads to another elliptical distribution.
  - The true predictive distribution can be recovered by linear reconciliation.
  - This need not be a projection.
--

- In the Gaussian case, Wickramasuriya (2023) proves that MinT is optimal w.r.t to log score.
--

- Otherwise, resort to numerical methods.
- Reconciliation mapping `$\psi$` can be found by optimising with respect to a scoring rule.

---

# An alternative

- Zambon et al. (2022) propose an alternative approach.
--

- Simply consider the base forecast, conditional on coherence being met.
--

- Sampling techniques (Importance sampling, MCMC) can be used to draw from the posterior.
--

- Research into the theoretical properties (of both approaches) is ongoing.

---

# Another alternative

- Rather than a 2 step approach consider an *end to end* approach Rangapuram, Werner, Benidis, Mercado, Gasthaus, and Januschowski (2021)
--

- Neural networks that include
  - A layer that guarantees coherence
  - Scoring rule as an objective function
--

- Not always applicable in organisational settings.

---

# Application areas

- Macroeconomics
  - Components of GDP
- Retail demand
  - Amazon, Walmart
- Mortality
  - Aggregate by geography or cause of death
- Healthcare
  - Accidents and Emergencies
--

- And others

---

# Summary

- Forecast reconciliation is an interesting area
- Despite progress, important questions remain unanswered
  - Theoretically
  - Methodologically
  - Empirically
--

- So jump on the bandwagon!

---

# References

.small[
Athanasopoulos, G. et al. (2017). "Forecasting with temporal
hierarchies". In: _European Journal of Operational Research_ 262.1, pp.
60-74.

Ben Taieb, S. et al. (2021). "Hierarchical Probabilistic Forecasting of
Electricity Demand With Smart Meter Data". In: _Journal of the American
Statistical Association_ 116, pp. 27-43.

Burba, D. et al. (2021). "A trainable reconciliation method for
hierarchical time-series". URL:
[https://arxiv.org/abs/2101.01329](https://arxiv.org/abs/2101.01329).

Byron, R. P. (1978). "The estimation of large social account matrices".
In: _Journal of the Royal Statistical Society, Series A_ 141.3, pp.
359-367.

Di Fonzo, T. et al. (2023). "Cross-temporal forecast reconciliation:
Optimal combination method and heuristic alternatives". In:
_International Journal of Forecasting_ 39.1, pp. 39-57.

Gross, C. W. et al. (1990). "Disaggregation methods to expedite product
line forecasting". In: _Journal of Forecasting_ 9.3, pp. 233-254.

Hollyman, R. et al. (2021). "Understanding forecast reconciliation".
In: _European Journal of Operational Research_ 294.1, pp. 149-160. DOI:
[10.1016/j.ejor.2021.01.017](https://doi.org/10.1016%2Fj.ejor.2021.01.017).
]

---

# References

.small[
Hyndman, R. J. et al. (2011). "Optimal combination forecasts for
hierarchical time series". In: _Computational Statistics and Data
Analysis_ 55.9, pp. 2579-2589.

Jeon, J. et al. (2019). "Probabilistic forecast reconciliation with
applications to wind power and electric load". In: _European Journal of
Operational Research_ 279.2, pp. 364-379.

Panagiotelis, A. et al. (2021). "Forecast reconciliation: A geometric
view with new insights on bias correction". In: _International Journal
of Forecasting_ 37.1, pp. 343-359.

Panagiotelis, A. et al. (2023). "Probabilistic forecast reconciliation:
properties, evaluation and score optimisation". In: _European Journal
of Operational Research_ 306.2, pp. 693-706.

Rangapuram, S. S. et al. (2021). "End-to-end learning of coherent
probabilistic forecasts for hierarchical time series". In: _Proceedings
of the 38th International Conference on Machine Learning, PMLR 139_. ,
pp. 8832-8843.

Schwarzkopf, A. B. et al. (1988). "Top-down versus bottom-up
forecasting strategies". In: _International Journal of Production
Research_ 26 (11), pp. 1833-1843.
]

---

# References

.small[
Spiliotis, E. et al. (2021). "Hierarchical forecast reconciliation with
machine learning". In: _Applied Soft Computing_ 112, p. 107756.

Stone, R. et al. (1942). "The precision of national income estimates".
In: _Review of Economic Studies_ 9.2, pp. 111-125. DOI:
[10.2307/2967664](https://doi.org/10.2307%2F2967664).

Wickramasuriya, S. L. (2023). "Probabilistic forecast reconciliation
under the Gaussian framework". In: _Journal of Business & Economic
Statistics_, pp. 1-14.

Wickramasuriya, S. L. et al. (2019). "Optimal Forecast Reconciliation
for Hierarchical and Grouped Time Series Through Trace Minimization".
In: _Journal of the American Statistical Association_ 114.526, pp.
804-819.

Zambon, L. et al. (2022). "Efficient probabilistic reconciliation of
forecasts for real-valued and count time series". URL:
[https://arxiv.org/abs/2210.02286](https://arxiv.org/abs/2210.02286).

Zhang, B. et al. (2023). "Discrete forecast reconciliation". URL:
[https://arxiv.org/abs/2305.18809](https://arxiv.org/abs/2305.18809).
]