Boosted mortality 
 models with age 
 and spatial shrinkage
Anastasios Panagiotelis
November, 2023
1

Joint work with

Li Li Han Li

The big storyStatistics v Machine LearningBoosting or domain-specific statistical models?

Humans v MachinesDoes domain knowledge about data structure matter?

Can't we just get along...
3

The big story

Statistics v Machine Learning
- Boosting or domain-specific statistical models?
Humans v Machines
- Does domain knowledge about data structure matter?
Can't we just get along...

The data4

Mortality data (all U.S.)

Image Title

Mortality data (selected states)

Image Title

ChallengesMortality generally trends downward
7

ChallengesMortality generally trends downwardBut not for all ages...
and not for all states

7

ChallengesMortality generally trends downwardBut not for all ages...
and not for all states

Age effects generally smooth over time
7

ChallengesMortality generally trends downwardBut not for all ages...
and not for all states

Age effects generally smooth over timeData are noisier for age/states with lower populations and fewer deaths

7

ChallengesMortality generally trends downwardBut not for all ages...
and not for all states

Age effects generally smooth over timeData are noisier for age/states with lower populations and fewer deaths

Different states, different patterns
7

ChallengesMortality generally trends downwardBut not for all ages...
and not for all states

Age effects generally smooth over timeData are noisier for age/states with lower populations and fewer deaths

Different states, different patterns  Neighboring states can have similar patterns

7

The model8

Lee Carter model

A popular mortality model is the Lee and Carter (1992) model.

$y_{x, t} = a_{x} + b_{x} κ_{t} + ϵ_{x, t}$

Lee Carter model

A popular mortality model is the Lee and Carter (1992) model.

$y_{x, t} = a_{x} + b_{x} κ_{t} + ϵ_{x, t}$

The $y_{x, t}$ are log mortality rates for age $x$ in year $t$ .
The $a_{x}$ are estimated as age-wise means
The $b_{x}$ are age weights, the $κ_{t}$ is a time trend
- Both estimated using SVD
The $ϵ_{x, t}$ are errors.

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
The idea of gradient boosting is to 
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
The idea of gradient boosting is to fit a weak learner, 
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
The idea of gradient boosting is to fit a weak learner, compute residuals, 
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
The idea of gradient boosting is to fit a weak learner, compute residuals, refit the weak learner 
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
The idea of gradient boosting is to fit a weak learner, compute residuals, refit the weak learner recompute residuals, 
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
The idea of gradient boosting is to fit a weak learner, compute residuals, refit the weak learner recompute residuals, etc.
10

Gradient BoostingConsider a prediction ft=(f0,t,…,f85+,t)′ft=(f0,t,…,f85+,t)′ with squared loss function
Lt(yt,ft)=(yt−ft)′(yt−ft)Lt(yt,ft)=(yt−ft)′(yt−ft)
Gradient proportional to residual (yt−ft)(yt−ft)
The idea of gradient boosting is to fit a weak learner, compute residuals, refit the weak learner recompute residuals, etc.
Prediction is ensemble of the weak learners
10

What is a weak learner?Typically trees. But can also be
11

What is a weak learner?Typically trees. But can also be  Logistic regression (Friedman, Hastie, and Tibshirani, 2000)
Generalized additive models (Tutz and Binder, 2006)
Copulas (Brant and Haff, 2022)

11

What is a weak learner?Typically trees. But can also be  Logistic regression (Friedman, Hastie, and Tibshirani, 2000)
Generalized additive models (Tutz and Binder, 2006)
Copulas (Brant and Haff, 2022)

Novel idea 1: Do gradient boosting with the Lee-Carter model.
11

Exploiting structureWe know certain things about mortality data.Mortality rates of similar ages are similar
Mortality rates of neighboring regions are similar due to local effects

12

Exploiting structureWe know certain things about mortality data.Mortality rates of similar ages are similar
Mortality rates of neighboring regions are similar due to local effects

Novel idea 2: Shrink forecasts together to borrow strength across nearby age groups and/or geographical regions
12

How to do shrinkage?

Add a penalty term to the objective function

$L_{t} (y_{t}, f_{t}) = (y_{t} - f_{t})^{'} (y_{t} - f_{t}) + λ f_{t}^{'} W f_{t}$

When Lee Carter model is refit, do not fit residuals, but residuals plus a term involving $W f_{t}$

How to do shrinkage?

Add a penalty term to the objective function

$L_{t} (y_{t}, f_{t}) = (y_{t} - f_{t})^{'} (y_{t} - f_{t}) + λ f_{t}^{'} W f_{t}$

When Lee Carter model is refit, do not fit residuals, but residuals plus a term involving $W f_{t}$
What is $W$ ?

How to do shrinkage?

Add a penalty term to the objective function

$L_{t} (y_{t}, f_{t}) = (y_{t} - f_{t})^{'} (y_{t} - f_{t}) + λ f_{t}^{'} W f_{t}$

When Lee Carter model is refit, do not fit residuals, but residuals plus a term involving $W f_{t}$
What is $W$ ?
- The Graph Laplacian.

How to do shrinkage?

Add a penalty term to the objective function

$L_{t} (y_{t}, f_{t}) = (y_{t} - f_{t})^{'} (y_{t} - f_{t}) + λ f_{t}^{'} W f_{t}$

When Lee Carter model is refit, do not fit residuals, but residuals plus a term involving $W f_{t}$
What is $W$ ?
- The Graph Laplacian.
Why does it make sense?

How to do shrinkage?

Add a penalty term to the objective function

$L_{t} (y_{t}, f_{t}) = (y_{t} - f_{t})^{'} (y_{t} - f_{t}) + λ f_{t}^{'} W f_{t}$

When Lee Carter model is refit, do not fit residuals, but residuals plus a term involving $W f_{t}$
What is $W$ ?
- The Graph Laplacian.
Why does it make sense?
- Need to think about neighborhoods.

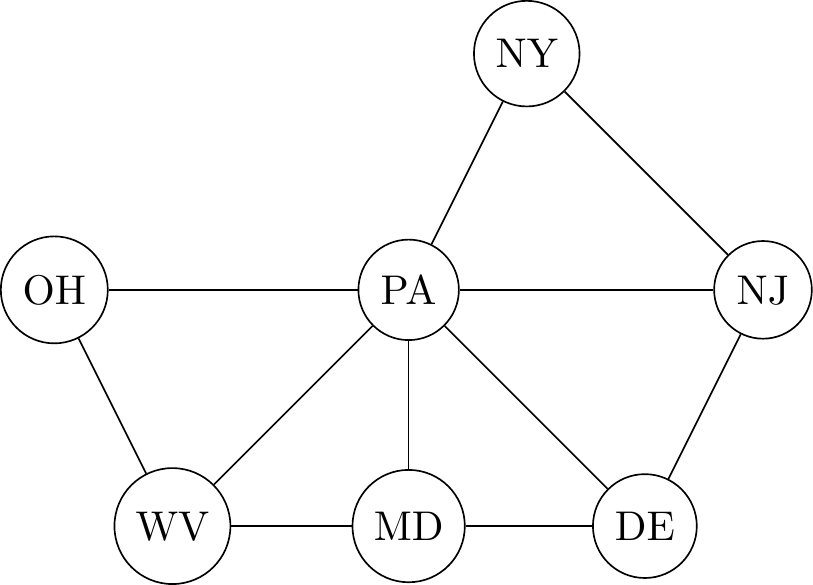
Graph Laplacian

Neighborhood structure for age

Neighborhood structure for states

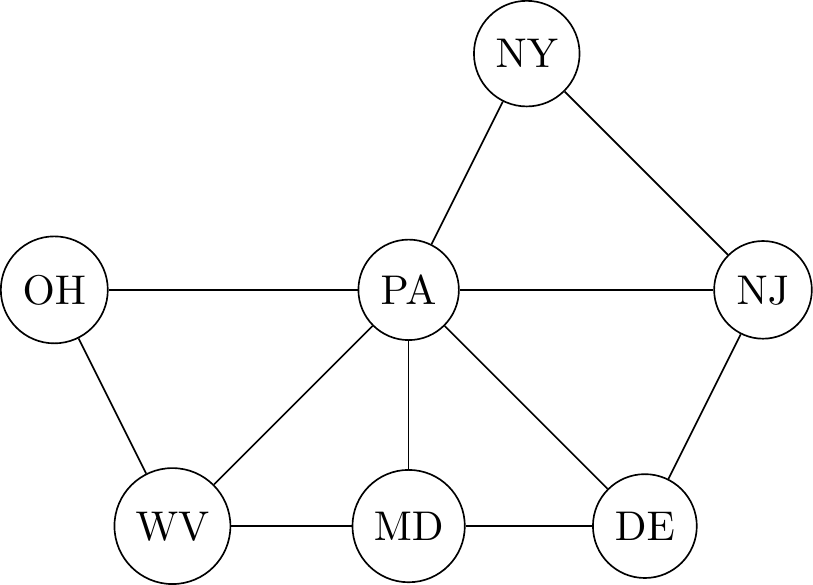
Graph Laplacian

Off diagonal elements are -1 if two nodes share an edge, 0 otherwise.
Diagonal elements are equal to number of neighbors.

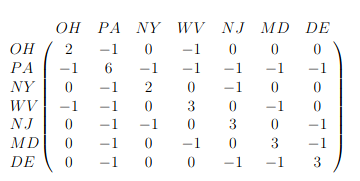
Effect on penalty

Residual for Maryland (MD) adds penalty

$(f_{M D, t} - f_{D E, t}) + (f_{M D, t} - f_{P A, t}) + (f_{M D, t} - f_{W V, t})$

Effect on penalty

Residual for Maryland (MD) adds penalty

$(f_{M D, t} - f_{D E, t}) + (f_{M D, t} - f_{P A, t}) + (f_{M D, t} - f_{W V, t})$

For age 50 add penalty

$(f_{50, t} - f_{49, t}) + (f_{50, t} - f_{51, t})$

Effect on penalty

Residual for Maryland (MD) adds penalty

$(f_{M D, t} - f_{D E, t}) + (f_{M D, t} - f_{P A, t}) + (f_{M D, t} - f_{W V, t})$

For age 50 add penalty

$(f_{50, t} - f_{49, t}) + (f_{50, t} - f_{51, t})$

When we fit the next Lee Carter model it will force forecasts to be closer to its neighbors forecasts.

Putting everything togetherWe can shrink across age and states using the following neighborhood structure
17

Putting everything togetherWe can shrink across age and states using the following neighborhood structureSame age, neighboring states are neighbors
Same state, neighboring age are neighbors

17

Putting everything togetherWe can shrink across age and states using the following neighborhood structureSame age, neighboring states are neighbors
Same state, neighboring age are neighbors

Mathematically we find the Cartesian product of the two graphs.
17

Putting everything togetherWe can shrink across age and states using the following neighborhood structureSame age, neighboring states are neighbors
Same state, neighboring age are neighbors

Mathematically we find the Cartesian product of the two graphs.
The graph Laplacian is found by a simple expression involving Kronecker products, see paper for details.
17

Results18

Empirical setupExpanding window from 1960−1997,...,20091960−1997,...,2009. 
19

Empirical setupExpanding window from 1960−1997,...,20091960−1997,...,2009. 
Make h=1,…,10h=1,…,10 step ahead forecasts.
19

Empirical setupExpanding window from 1960−1997,...,20091960−1997,...,2009. 
Make h=1,…,10h=1,…,10 step ahead forecasts.
Use Lee Carter (LC) and three other benchmarksHyndman and Ullah (2007) (H-U)
Hyndman, Booth, and Yasmeen (2013) (H-B-Y)
LightGBM (a popular tree based boosting method).

19

Empirical setupConsider four new approaches:Gradient boosted Lee Carter (GBLC)
with age shrinkage (GBLC-age)
with state shrinkage (GBLC-state)
with age and state shrinkage (GBLC-age-state)

20

Summary of resultsAt a national level, GBLC and GBLC-age significantly outperform everything.
At horizons 1 and 4, GBLC-age is significantly better than GBLC.
At a state level, LightGBM, GBLC-age and GBLC-age-state significantly outperform everything.
For longer horizons, GBLC-age-state outperforms even LightGBM an GBLC-age.
These results are based on model confidence sets
21

National level results

For presentation purposes take averages across 20 year age bands. Figures show improvement in MASE

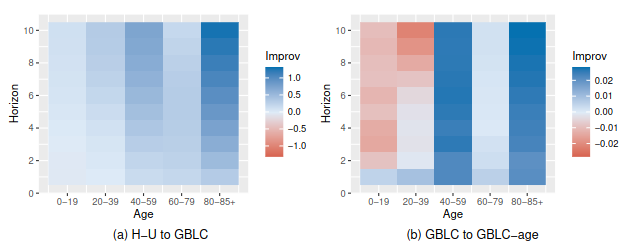
Image Title

State level results

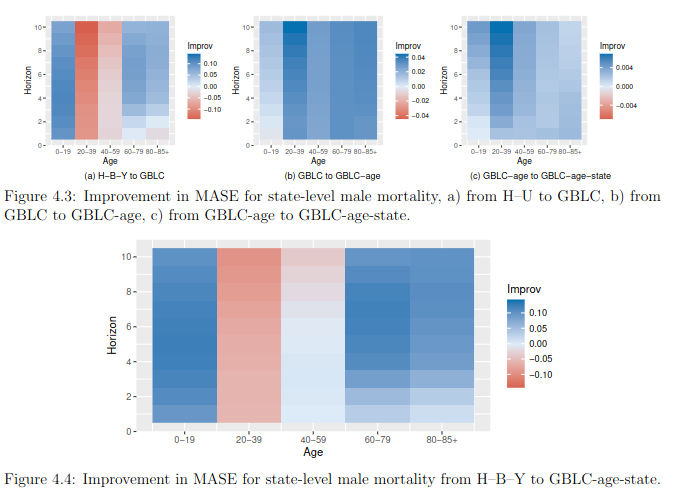
Image Title

State level results

Improvement from GBLC to GBLC-state

Image Title

ConclusionsIf you have a forecasting model that works in a specific domain, try boosting.
If you have structure in what you are trying to forecast, consider shrinkage.
25

Conclusions

If you have a forecasting model that works in a specific domain, try boosting.
If you have structure in what you are trying to forecast, consider shrinkage.

References

Brant, S. B. et al. (2022). Copulaboost: additive modeling with copula-based model components. arXiv: 2208.04669 [stat.ME].

Friedman, J. et al. (2000). "Additive logistic regression: A statistical view of boosting (With discussion and a rejoinder by the authors)". In: The Annals of Statistics 28.2, pp. 337 - 407.

Hyndman, R. J. et al. (2013). "Coherent mortality forecasting: the product-ratio method with functional time series models". In: Demography 50.1, pp. 261-283.

Hyndman, R. J. et al. (2007). "Robust forecasting of mortality and fertility rates: A functional data approach". In: Computational Statistics & Data Analysis 51.10, pp. 4942-4956.

Lee, R. D. et al. (1992). "Modeling and forecasting US mortality". In: Journal of the American Statistical Association 87.419, pp. 659-671.

Tutz, G. et al. (2006). "Generalized Additive Modeling with Implicit Variable Selection by Likelihood-Based Boosting". In: Biometrics 62.4, pp. 961-971.

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Boosted mortality models with age and spatial shrinkage

Anastasios Panagiotelis

November, 2023

Joint work with

The big story

The big story

The data

Mortality data (all U.S.)

Mortality data (selected states)

Challenges

Challenges

Challenges

Challenges

Challenges

Challenges

The model

Lee Carter model

Lee Carter model

Gradient Boosting

Gradient Boosting

Gradient Boosting

Gradient Boosting

Gradient Boosting

Gradient Boosting

Gradient Boosting

Gradient Boosting

Gradient Boosting

Gradient Boosting

What is a weak learner?

What is a weak learner?

What is a weak learner?

Exploiting structure

Exploiting structure

How to do shrinkage?

How to do shrinkage?

How to do shrinkage?

How to do shrinkage?

How to do shrinkage?

Graph Laplacian

Graph Laplacian

Effect on penalty

Effect on penalty

Effect on penalty

Putting everything together

Putting everything together

Putting everything together

Putting everything together

Results

Empirical setup

Empirical setup

Empirical setup

Empirical setup

Summary of results

National level results

State level results

State level results

Conclusions

Conclusions

References

Joint work with

Help

Boosted mortality
models with age
and spatial shrinkage