+ - 0:00:00
Notes for current slide
Notes for next slide

Detecting anomalies
in smart meter data
via manifold learning

Anastasios Panagiotelis

University of Sydney

1

Smart Meter

  • Smart meters measure electricity usage in a building.
  • Need to detect anomalous electricity usage.
  • Scalable to millions of buildings.

2

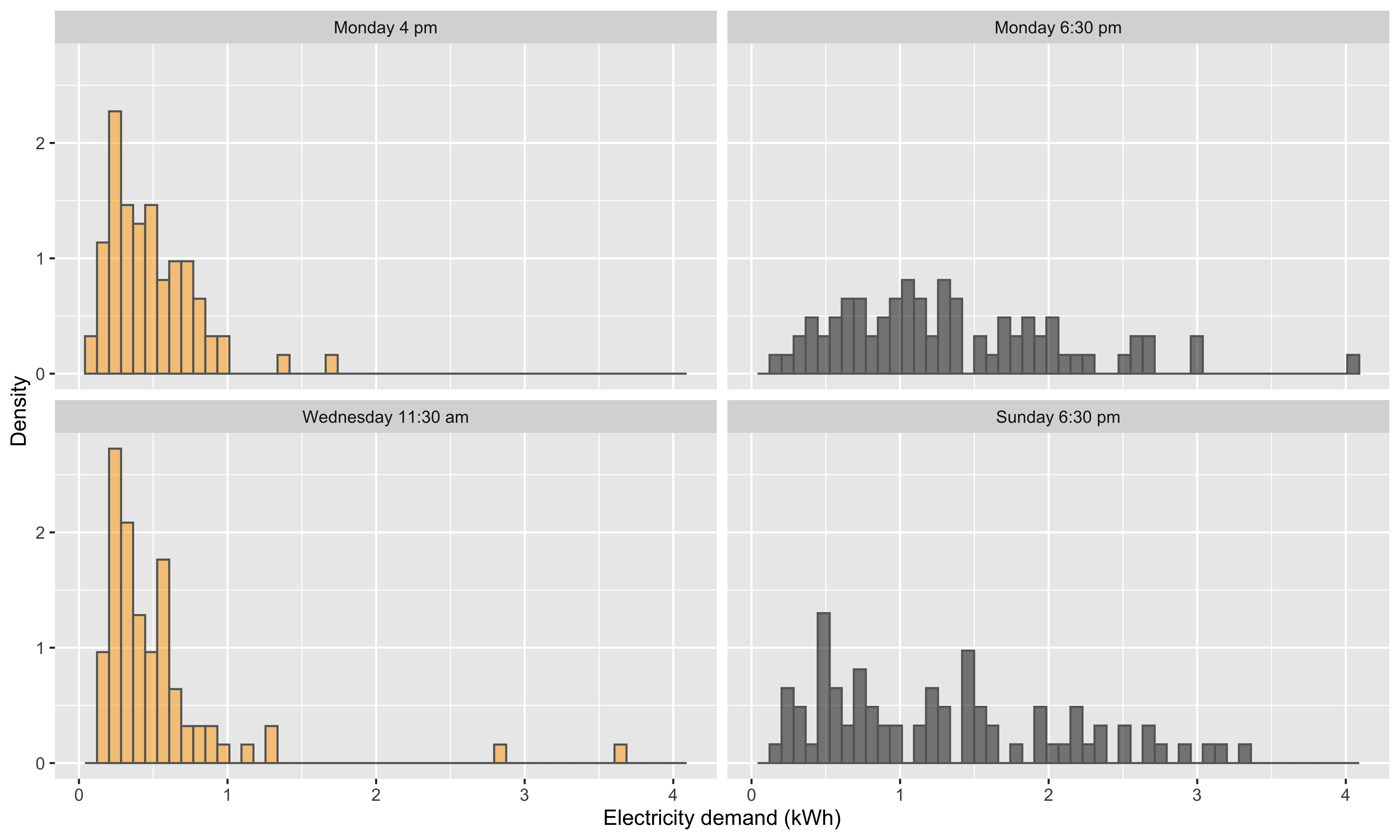
Smart Meter data

  • Three housholds in an Irish dataset

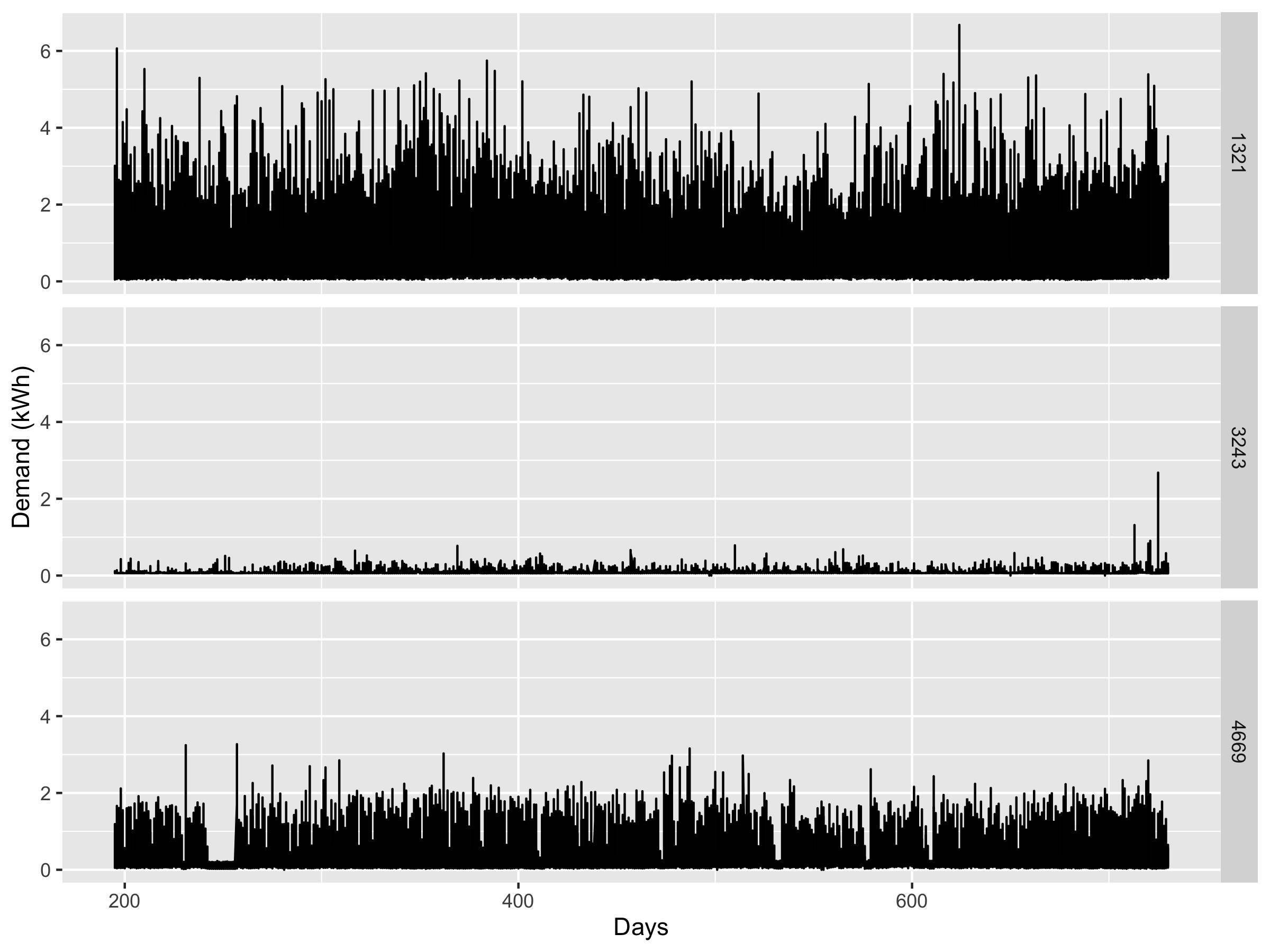
3

Smart Meter data

  • Interested in distribution

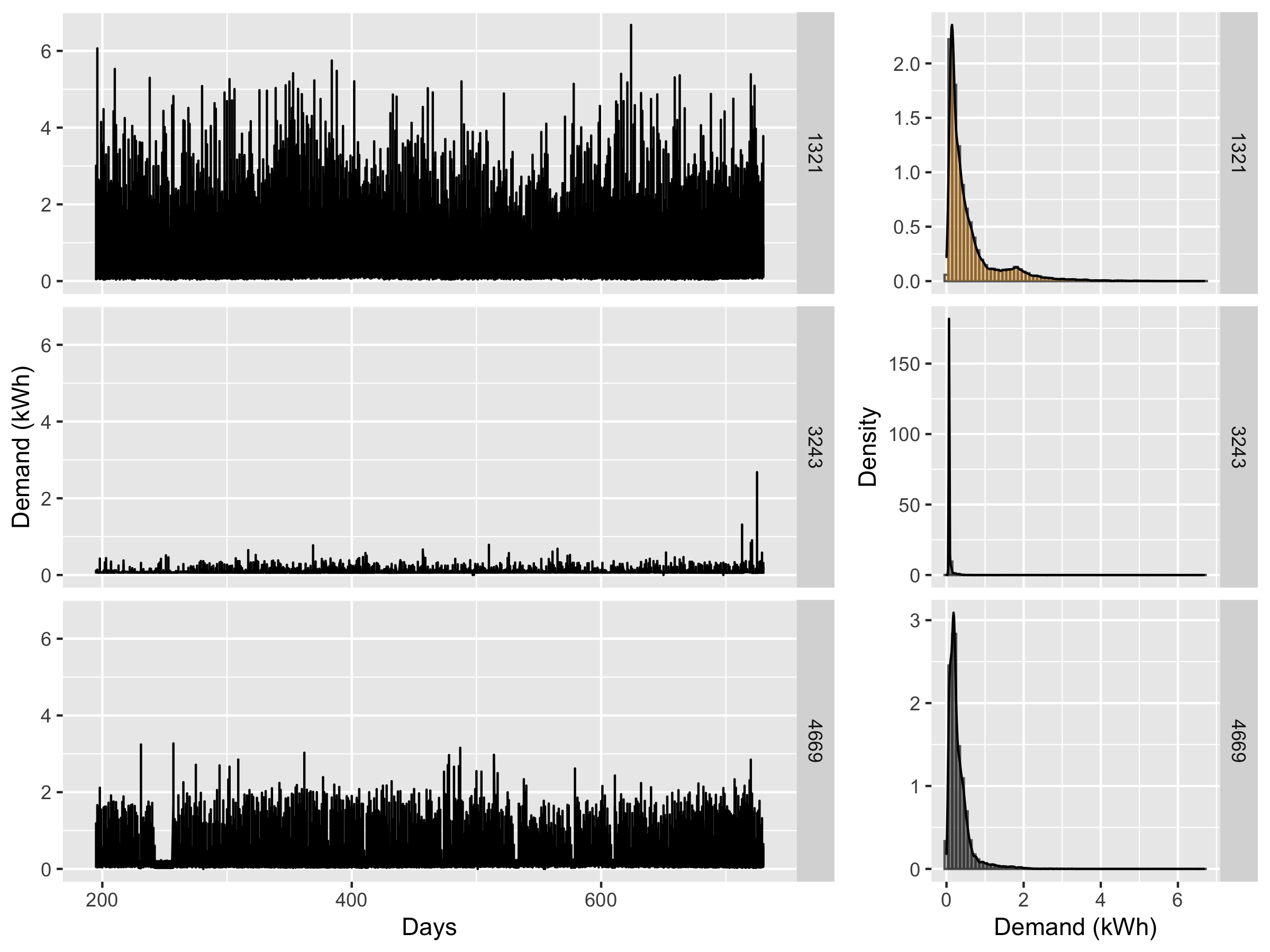
4

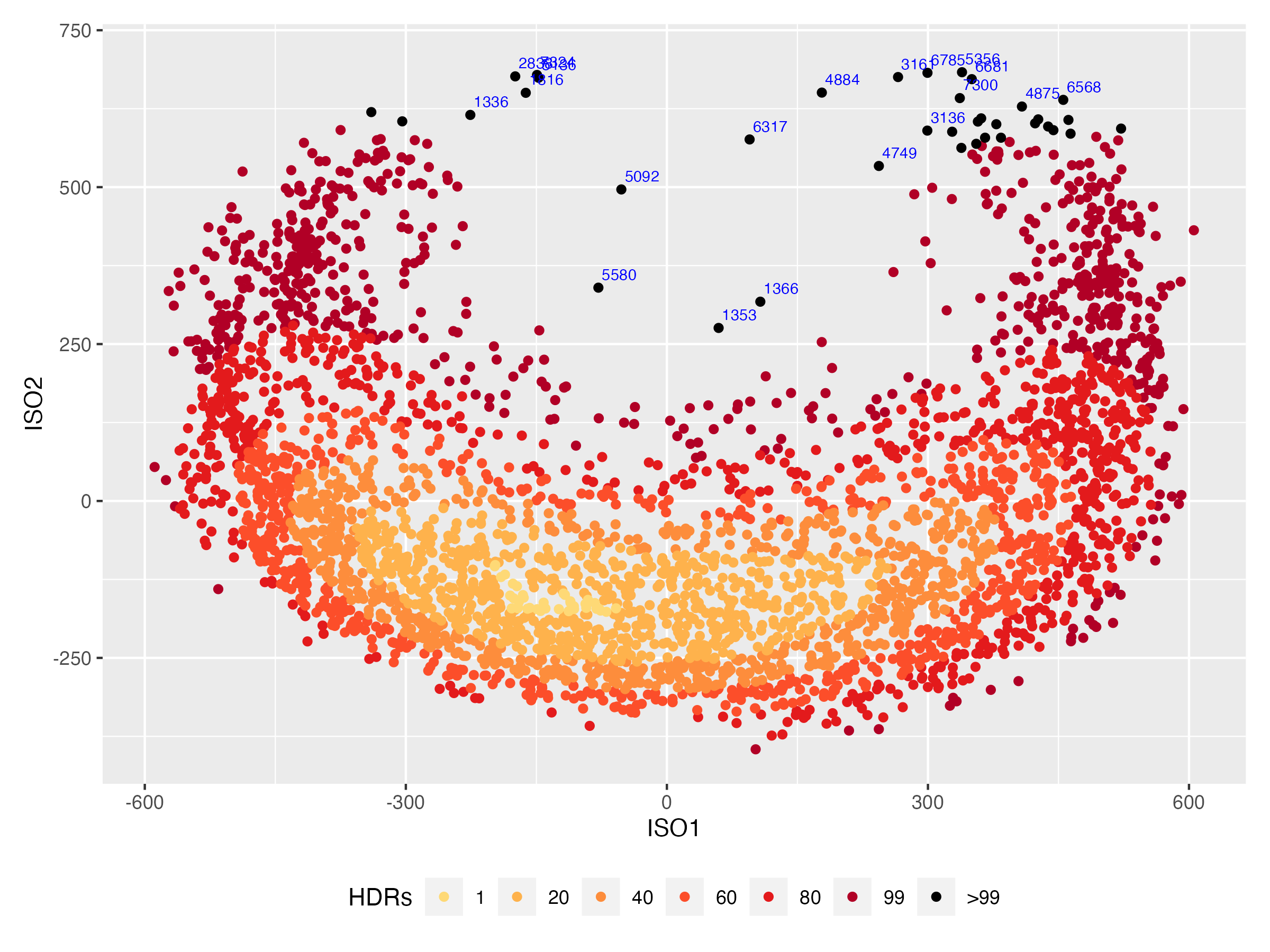
Visualisation

5

Interpretation

  • Each dot represents the probability distribution of electricity usage for a single household.
6

Interpretation

  • Each dot represents the probability distribution of electricity usage for a single household.
  • The colors depend on the value of a kernel density estimate of the points.
6

Interpretation

  • Each dot represents the probability distribution of electricity usage for a single household.
  • The colors depend on the value of a kernel density estimate of the points.
  • The 'typical' household comes from the middle of the distribution.
6

Interpretation

  • Each dot represents the probability distribution of electricity usage for a single household.
  • The colors depend on the value of a kernel density estimate of the points.
  • The 'typical' household comes from the middle of the distribution.
  • The 'anomalous' households comes from edges of the distribution.
6

Interpretation

  • Each dot represents the probability distribution of electricity usage for a single household.
  • The colors depend on the value of a kernel density estimate of the points.
  • The 'typical' household comes from the middle of the distribution.
  • The 'anomalous' households comes from edges of the distribution.
  • But how do we get that plot?
6

Outline

  • Manifold Learning
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
    • Isomap algorithm
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
    • Isomap algorithm
  • Statistical manifolds
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
    • Isomap algorithm
  • Statistical manifolds
    • Hellinger distance estimator
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
    • Isomap algorithm
  • Statistical manifolds
    • Hellinger distance estimator
    • Why it is fast
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
    • Isomap algorithm
  • Statistical manifolds
    • Hellinger distance estimator
    • Why it is fast
  • Application
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
    • Isomap algorithm
  • Statistical manifolds
    • Hellinger distance estimator
    • Why it is fast
  • Application
    • One household
7

Outline

  • Manifold Learning
    • Multidimensional Scaling
    • Isomap algorithm
  • Statistical manifolds
    • Hellinger distance estimator
    • Why it is fast
  • Application
    • One household
    • All households
7

Dimension reduction

8

Idea

  • Data are multivariate, i.e. xi∈Rp where p is large and i=1,2,…,n.
9

Idea

  • Data are multivariate, i.e. xi∈Rp where p is large and i=1,2,…,n.
    • Consider n firms with p financial indicators
9

Idea

  • Data are multivariate, i.e. xi∈Rp where p is large and i=1,2,…,n.
    • Consider n firms with p financial indicators
  • Construct new data yi∈Rd where d<<p.
9

Idea

  • Data are multivariate, i.e. xi∈Rp where p is large and i=1,2,…,n.
    • Consider n firms with p financial indicators
  • Construct new data yi∈Rd where d<<p.
  • How might we do this?
9

Distances

  • Close observations in input space should be close in output space.
10

Distances

  • Close observations in input space should be close in output space.
  • Euclidean distance is a measure of similarity.
10

Distances

  • Close observations in input space should be close in output space.
  • Euclidean distance is a measure of similarity.
  • Inputs: δij=(xi−xj)′(xi−xj)
10

Distances

  • Close observations in input space should be close in output space.
  • Euclidean distance is a measure of similarity.
  • Inputs: δij=(xi−xj)′(xi−xj)
  • Outputs: dij=(yi−yj)′(yi−yj)
10

Distances

  • Close observations in input space should be close in output space.
  • Euclidean distance is a measure of similarity.
  • Inputs: δij=(xi−xj)′(xi−xj)
  • Outputs: dij=(yi−yj)′(yi−yj)
  • Construct y so that dij approximate δij
10

Criterion

Minimise:

∑i,j(δij2−dij2)

Solved by

11

Criterion

Minimise:

∑i,j(δij2−dij2)

Solved by

  1. Putting δij in a matrix Δ
  2. Double centering Δ
  3. Finding eigenvectors.
11

Non-Euclidean

  • What if input distances δij are not Euclidean?
12

Non-Euclidean

  • What if input distances δij are not Euclidean?
  • Can put them in Δ anyway
12

Non-Euclidean

  • What if input distances δij are not Euclidean?
  • Can put them in Δ anyway
  • Optimise a slightly different objective, but still get a good representation.
12

Non-Euclidean

  • What if input distances δij are not Euclidean?
  • Can put them in Δ anyway
  • Optimise a slightly different objective, but still get a good representation.
  • Output distances dij still approximate input distances δij
12

Manifold learning

  • What if data lie on some non-linear d-dimensional surface in p-dimensional space.
13

Manifold learning

  • What if data lie on some non-linear d-dimensional surface in p-dimensional space.
  • Think of the surface of a sphere (2-dimensional) in space (3-dimensional).
13

Manifold learning

  • What if data lie on some non-linear d-dimensional surface in p-dimensional space.
  • Think of the surface of a sphere (2-dimensional) in space (3-dimensional).
  • Euclidean distance is no longer appropriate
13

Manifold learning

  • What if data lie on some non-linear d-dimensional surface in p-dimensional space.
  • Think of the surface of a sphere (2-dimensional) in space (3-dimensional).
  • Euclidean distance is no longer appropriate
  • Should instead use the geodesic distance.
13

Manifold learning

  • What if data lie on some non-linear d-dimensional surface in p-dimensional space.
  • Think of the surface of a sphere (2-dimensional) in space (3-dimensional).
  • Euclidean distance is no longer appropriate
  • Should instead use the geodesic distance.
  • This is the aim of ISOMAP.
13

Toy example

Consider the following data

14

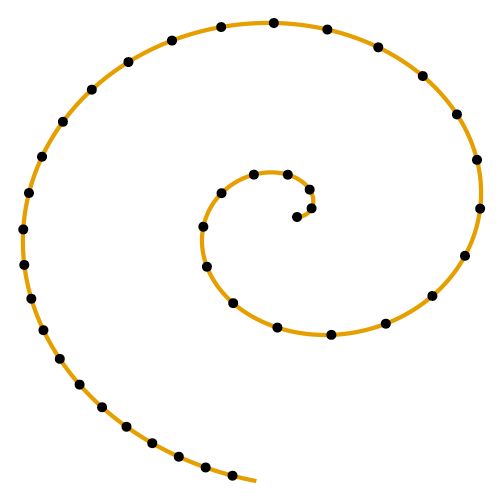
Manifold

Lying on a manifold.

15

Euclidean distance

Blue points close in ambient space.

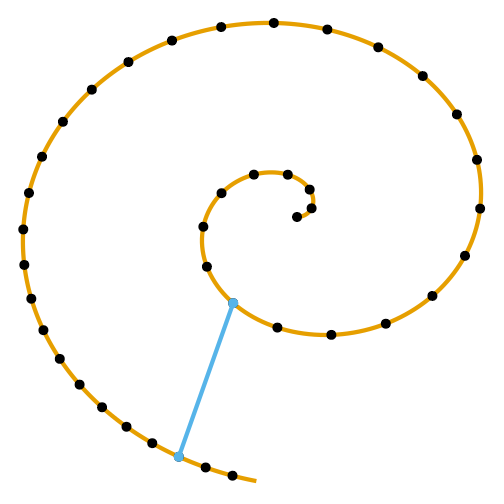
16

Geodesic Distance

But not on manifold.

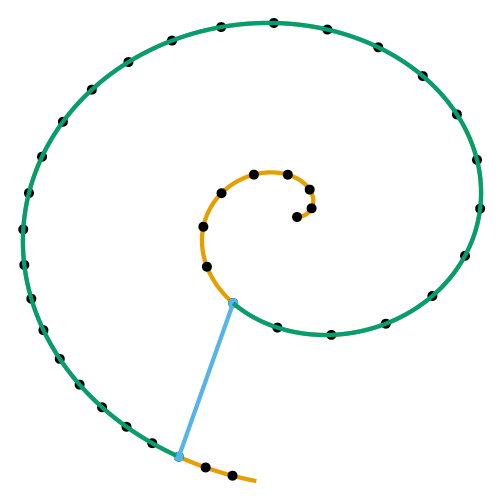
17

Input distances

  • Classical MDS would use the distance in blue as an input
18

Input distances

  • Classical MDS would use the distance in blue as an input
  • The idea behind Isomap is to use the distance in green as an input.
18

Input distances

  • Classical MDS would use the distance in blue as an input
  • The idea behind Isomap is to use the distance in green as an input.
  • However to compute the geodesic (green) distance we need to know the manifold.
18

Input distances

  • Classical MDS would use the distance in blue as an input
  • The idea behind Isomap is to use the distance in green as an input.
  • However to compute the geodesic (green) distance we need to know the manifold.
  • Instead we approximate the geodesic distance
18

Geodesic Distance

Geodesic can be approximated.

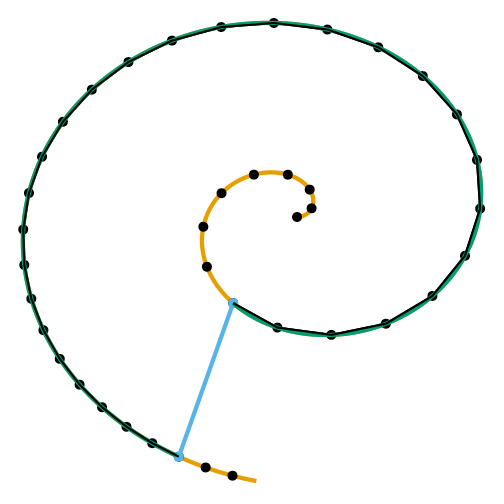
19

Geodesic Distance

Try zooming.

20

Approximate Geodesic

  • Find the graph of nearest neighbors
21

Approximate Geodesic

  • Find the graph of nearest neighbors
    • Neighbourhood within a ϵ-ball
    • K-Nearest neighbours
21

Approximate Geodesic

  • Find the graph of nearest neighbors
    • Neighbourhood within a ϵ-ball
    • K-Nearest neighbours
  • As edge weights use the distance between neighbors
21

Approximate Geodesic

  • Find the graph of nearest neighbors
    • Neighbourhood within a ϵ-ball
    • K-Nearest neighbours
  • As edge weights use the distance between neighbors
  • Approximate geodesic distance by finding shortest path
21

Example

  • ISOMAP is just one manifold learning algorithm.
22

Example

  • ISOMAP is just one manifold learning algorithm.
  • Others include:
    • LLE
    • Laplacian Eigenmaps
    • t-SNE
    • ...
22

Example

  • ISOMAP is just one manifold learning algorithm.
  • Others include:
    • LLE
    • Laplacian Eigenmaps
    • t-SNE
    • ...
  • These algorithms (and many others) use the nearest neighbor graph.
22

Statistical Manifolds

23

Statistical manifolds

  • A statistical manifold is a manifold with elements that are probability distributions
24

Statistical manifolds

  • A statistical manifold is a manifold with elements that are probability distributions
  • Can no longer think of the inputs as being p-dimensional vectors
24

Statistical manifolds

  • A statistical manifold is a manifold with elements that are probability distributions
  • Can no longer think of the inputs as being p-dimensional vectors
  • Can no longer think of Euclidean distance as being a distance between input points.
24

Statistical manifolds

  • A statistical manifold is a manifold with elements that are probability distributions
  • Can no longer think of the inputs as being p-dimensional vectors
  • Can no longer think of Euclidean distance as being a distance between input points.
  • We can use other measures of distance.
24

Hellinger Distance

  • Distance between two distributions given by

Hi,j2=12∫(pi(z)−pj(z))2dz

25

Hellinger Distance

  • Distance between two distributions given by

Hi,j2=12∫(pi(z)−pj(z))2dz

  • Where pi(x) and pj(x) are densities corresponding to observation i and j respectively.
25

Hellinger Distance

  • Distance between two distributions given by

Hi,j2=12∫(pi(z)−pj(z))2dz

  • Where pi(x) and pj(x) are densities corresponding to observation i and j respectively.
  • Need to estimate using data zi,1,zi,2,…,zi,Ti∼pi and zj,1,zj,2,…,zj,Tj∼pj.
25

Our estimator

  • Pool all the data zi,1,zi,2,…zi,Ti∀i=1,2,…,n together.
  • Find L equal probability partitions of the pooled data Il=(γl−1,γl−1] and let

πi,l=12Ti∑tI{zi,t∈Il}

26

Our estimator

  • Pool all the data zi,1,zi,2,…zi,Ti∀i=1,2,…,n together.
  • Find L equal probability partitions of the pooled data Il=(γl−1,γl−1] and let

πi,l=12Ti∑tI{zi,t∈Il}

  • Estimator is

H^i,j=∑l(πi,l−πj,l)2

26

Estimator

  • We prove this estimator is consistent as the number of observations Ti and number of partitions L goes to infinity.
27

Estimator

  • We prove this estimator is consistent as the number of observations Ti and number of partitions L goes to infinity.
  • This is not the only estimator of Hellinger distance.
27

Estimator

  • We prove this estimator is consistent as the number of observations Ti and number of partitions L goes to infinity.
  • This is not the only estimator of Hellinger distance.
  • What makes it special is that it 'looks like' a Euclidean distance.
27

Estimator

  • We prove this estimator is consistent as the number of observations Ti and number of partitions L goes to infinity.
  • This is not the only estimator of Hellinger distance.
  • What makes it special is that it 'looks like' a Euclidean distance.
  • This is important for computational reasons.
27

Nearest neighbour graph

  • Recall that manifold learning algorithms require finding a nearest neighbor graph.
28

Nearest neighbour graph

  • Recall that manifold learning algorithms require finding a nearest neighbor graph.
  • A naive way to do this would be to compute all N2 pairwise distances.
28

Nearest neighbour graph

  • Recall that manifold learning algorithms require finding a nearest neighbor graph.
  • A naive way to do this would be to compute all N2 pairwise distances.
  • A smarter way is to use an algorithm such as k-d trees.
28

Nearest neighbour graph

  • Recall that manifold learning algorithms require finding a nearest neighbor graph.
  • A naive way to do this would be to compute all N2 pairwise distances.
  • A smarter way is to use an algorithm such as k-d trees.
  • This only requires computing O(Nlog(N)) pairwise distances.
28

Nearest neighbour graph

  • Recall that manifold learning algorithms require finding a nearest neighbor graph.
  • A naive way to do this would be to compute all N2 pairwise distances.
  • A smarter way is to use an algorithm such as k-d trees.
  • This only requires computing O(Nlog(N)) pairwise distances.
  • But it only works for a few distance metrics (one of which is Euclidean).
28

Approximate nearest neighbours

  • Further speed up is possible via approximate nearest neighbors.
29

Approximate nearest neighbours

  • Further speed up is possible via approximate nearest neighbors.
  • May find an 'incorrect' nearest neighbor, but this is still guaranteed to be within 1+ϵ of the true nearest neighbor.
29

Approximate nearest neighbours

  • Further speed up is possible via approximate nearest neighbors.
  • May find an 'incorrect' nearest neighbor, but this is still guaranteed to be within 1+ϵ of the true nearest neighbor.
  • We test for robustness of results to using ANN.
29

Approximate nearest neighbours

  • Further speed up is possible via approximate nearest neighbors.
  • May find an 'incorrect' nearest neighbor, but this is still guaranteed to be within 1+ϵ of the true nearest neighbor.
  • We test for robustness of results to using ANN.
  • We also use a more recent algorithm known as ANNOY
29

Application

30

Single household

  • Consider a single household.
  • Each 'observation' is the distribution corresponding to an hour of week, over many weeks.
  • Here N=336 and T≈535
  • Use ISOMAP with exact nearest neighbors, ANN and ANNOY
31

Results

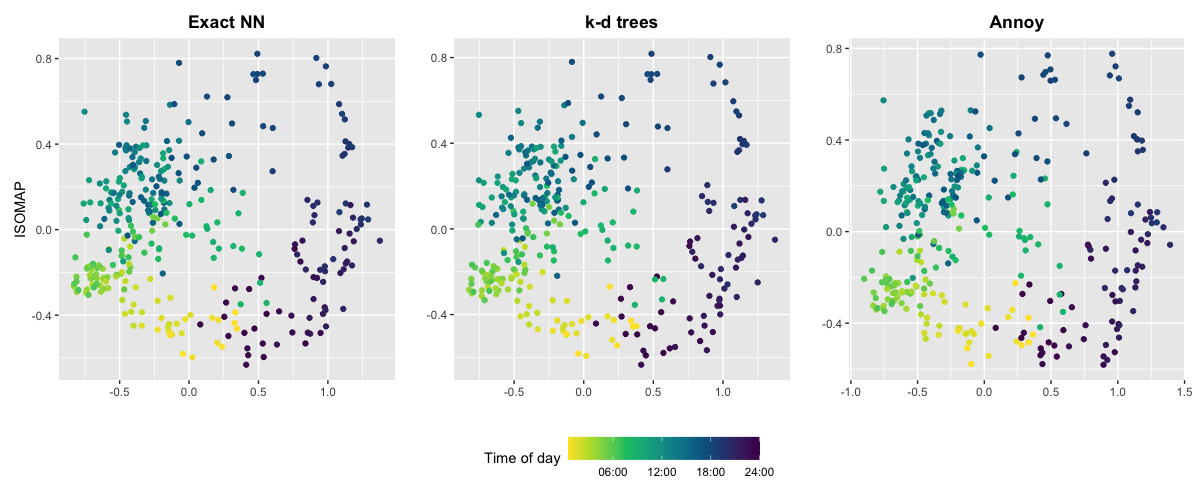
32

Results

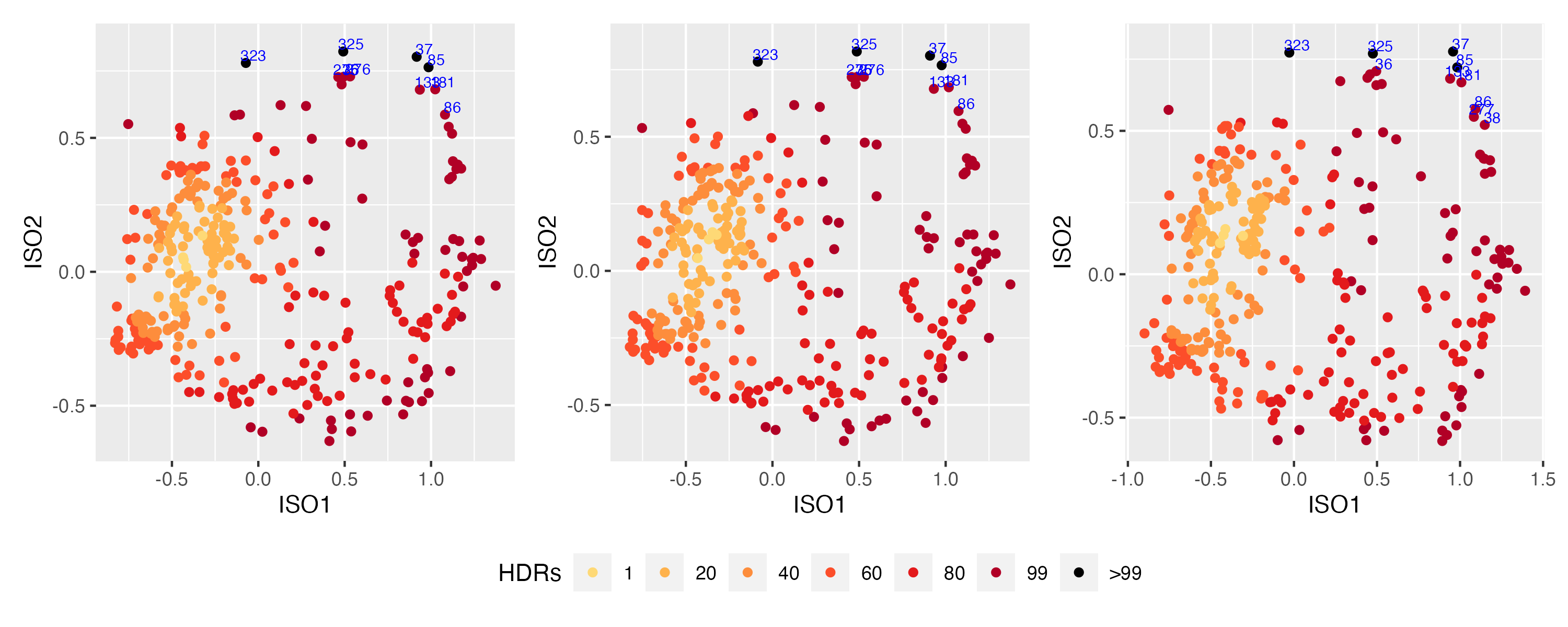
33

Typical and anomalous hours

34

Speed

Isomap LLE Laplacian Eigenmaps Hessian LLE t-SNE UMAP
Exact NN with brute-force 2.760 5.134 2.944 2.087 1.918 2.367
Exact NN with k-d trees 2.360 2.609 2.295 1.669 1.596 2.089
ANN k-d trees 2.351 2.986 2.302 1.663 1.601 2.048
ANN Annoy 1.942 3.093 2.378 1.695 1.647 2.125
35

Accuracy

Isomap LLE Laplacian Eigenmaps Hessian LLE t-SNE UMAP
Exact NN 0.943 0.709 0.885 0.882 0.935 0.924
ANN k-d trees 0.942 0.718 0.891 0.885 0.902 0.933
ANN Annoy 0.938 0.746 0.886 0.873 0.939 0.929
36

All households

  • Consider all household.
  • Each 'observation' is the distribution corresponding to an household.
  • Here N=3639 and T≈179760
  • Use ISOMAP with exact nearest neighbors, ANN and ANNOY
37

Results

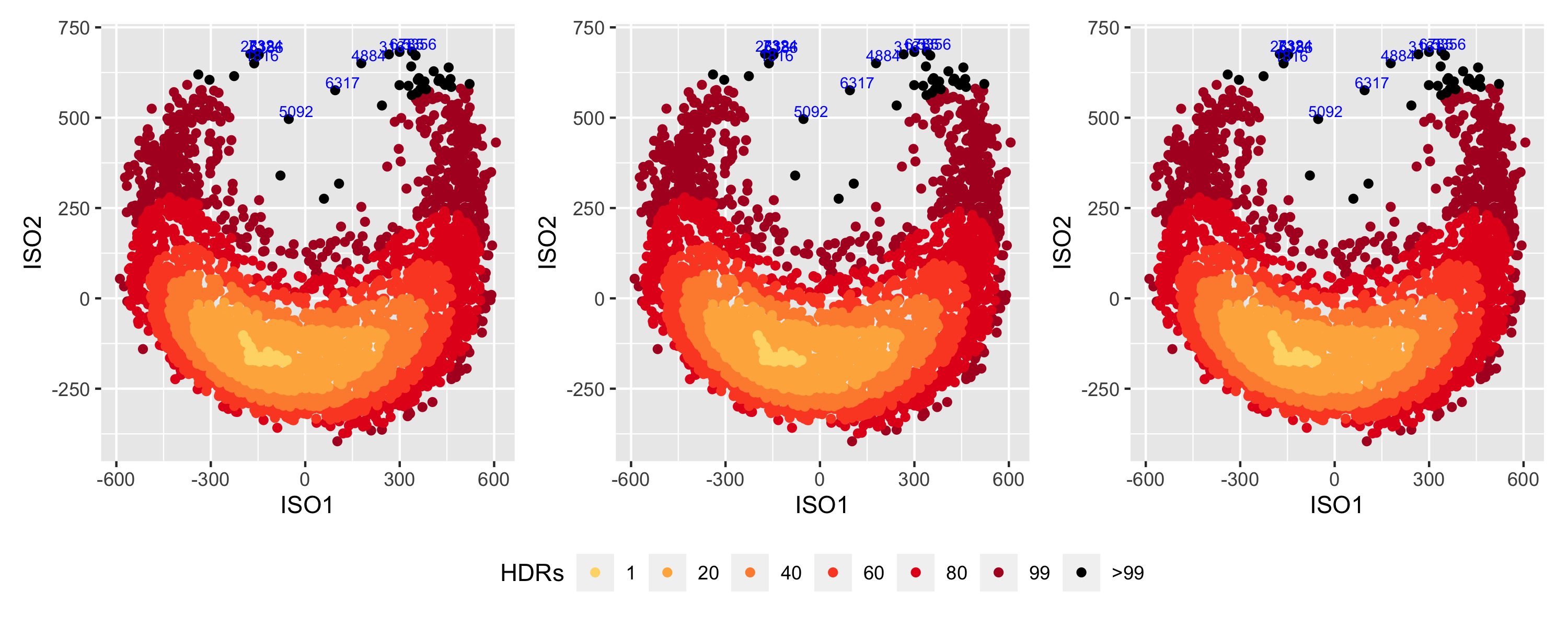
38

Speed

Isomap LLE Laplacian Eigenmaps Hessian LLE t-SNE UMAP
Exact NN with brute-force 4773.4 4967.4 4725.2 5930.4 4739.6 748.6
Exact NN with k-d trees 755.8 1038.2 749.6 1204.1 747.7 744.3
ANN k-d trees 755.7 1041.0 751.5 1208.7 747.8 741.7
ANN Annoy 1670.2 1947.3 1656.1 2363.7 1557.1 1675.3
39

Accuracy

Method Isomap LLE Laplacian Eigenmaps Hessian LLE t-SNE UMAP
Exact NN 0.926 0.911 0.880 0.579 0.914 0.943
ANN k-d trees 0.926 0.911 0.880 0.579 0.919 0.943
ANN Annoy 0.926 0.911 0.880 0.578 0.907 0.943
40

Conclusions

  • We have a way of visualising and finding anomalies for statistical manifolds
41

Conclusions

  • We have a way of visualising and finding anomalies for statistical manifolds
  • Relies on a consistent estimator of Hellinger distance
41

Conclusions

  • We have a way of visualising and finding anomalies for statistical manifolds
  • Relies on a consistent estimator of Hellinger distance
  • Has computational advantages that exploit Nearest Neighbor algorithms
41

Conclusions

  • We have a way of visualising and finding anomalies for statistical manifolds
  • Relies on a consistent estimator of Hellinger distance
  • Has computational advantages that exploit Nearest Neighbor algorithms
  • Further computational improvements possible with ANN and there is little tradeoff on accuracy.
41

Questions?

42

Smart Meter

  • Smart meters measure electricity usage in a building.
  • Need to detect anomalous electricity usage.
  • Scalable to millions of buildings.

2
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow