Basic Visualisation in R
Data Visualisation and Analytics
Anastasios Panagiotelis and Lauren Kennedy
Lecture 3
1
The Grammar of Graphics
2
The grammar of graphics
- At first using
ggplot2can seem too complicated. - Once mastered it can be used to very easily create detailed plots.
- It is built on the ideas of Grammar of Graphics a text by Leland Wilkinson.
- The objective is to find an abstract set of rules for creating almost any graphic.
3
Data
- The starting point for all visualisation is a dataset.
4
Data
- The starting point for all visualisation is a dataset.
- In these slides, we will consider the datasets
diamonds,mpgandeconomicswhich come built in with theggplot2package.
4
Data
- The starting point for all visualisation is a dataset.
- In these slides, we will consider the datasets
diamonds,mpgandeconomicswhich come built in with theggplot2package. - Later on we learn how to read in data.
4
Data
- The starting point for all visualisation is a dataset.
- In these slides, we will consider the datasets
diamonds,mpgandeconomicswhich come built in with theggplot2package. - Later on we learn how to read in data.
- The
diamondsdata contains data on the price, size and quality of over 50000 diamonds.
4
Aes and Geom
- Think of an aesthetic (or aes) as a way of perceiving a variable:
- Position on x or y axis
- Color
- Size
- Think of a geometry (or geom) as a way of representing a variable:
- Points
- Lines
ggplotmaps aesthetics to geometries
5
Histogram
6
Histogram
- Consider a histogram of the variable price
7
Histogram
- Consider a histogram of the variable price
- In a histogram, values of the variable we are interested in lie along the horizontal (x) axis.
7
Histogram
- Consider a histogram of the variable price
- In a histogram, values of the variable we are interested in lie along the horizontal (x) axis.
- The histogram creates bins then counts the number of observations in each bin.
7
Histogram
- Consider a histogram of the variable price
- In a histogram, values of the variable we are interested in lie along the horizontal (x) axis.
- The histogram creates bins then counts the number of observations in each bin.
- To get started type
ggplot(data = diamonds,mapping = aes(x=price))7
What do we see?
8
What do we see?
- We do have an x axis with a label price and some values.
9
What do we see?
- We do have an x axis with a label price and some values.
- Otherwise we see nothing.
9
What do we see?
- We do have an x axis with a label price and some values.
- Otherwise we see nothing.
- We need to add a geometry to the plot.
9
What do we see?
- We do have an x axis with a label price and some values.
- Otherwise we see nothing.
- We need to add a geometry to the plot.
- We do this with the
geom_histogramfunction.
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram()9
What do we see?
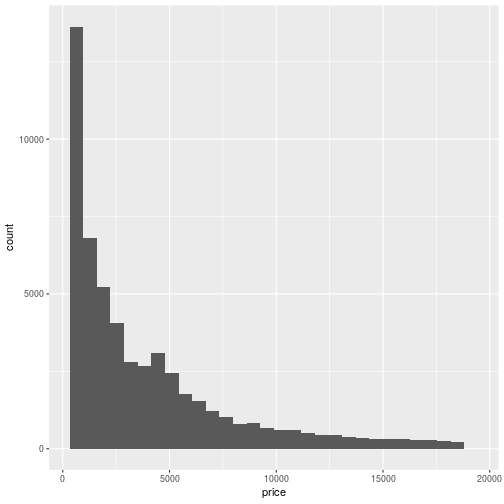
10
Modification
- Suppose want to use a different number of bins or change the color of the bins?
11
Modification
- Suppose want to use a different number of bins or change the color of the bins?
- These are not features of the data or the aes
11
Modification
- Suppose want to use a different number of bins or change the color of the bins?
- These are not features of the data or the aes
- These are features of the geom.
11
Modification
- Suppose want to use a different number of bins or change the color of the bins?
- These are not features of the data or the aes
- These are features of the geom.
- So these are controlled by arguments in the
geom_histogramfunction.
11
Change bins
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram(bins = 5)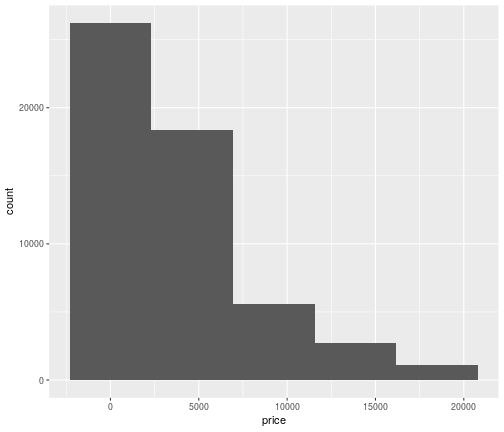
12
Change boundary
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram(bins = 5, boundary=0)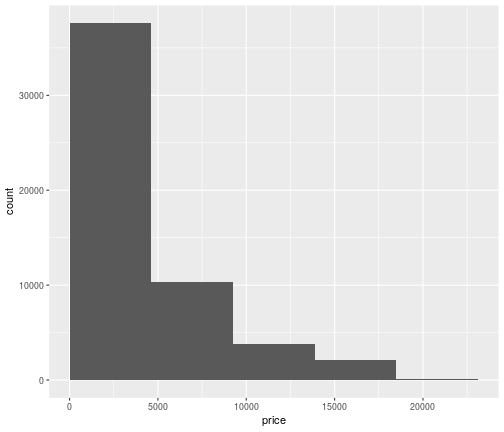
13
Change binwidth
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram(binwidth = 500)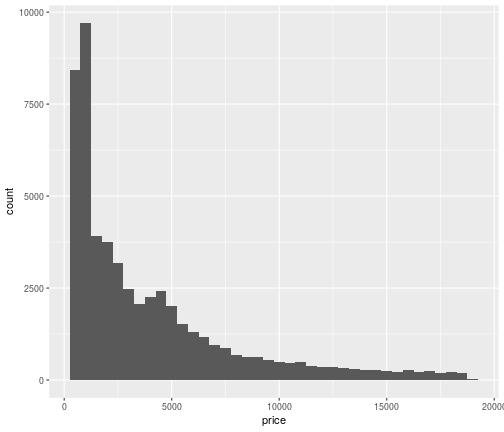
14
Change color
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram(binwidth = 500,fill = 'red')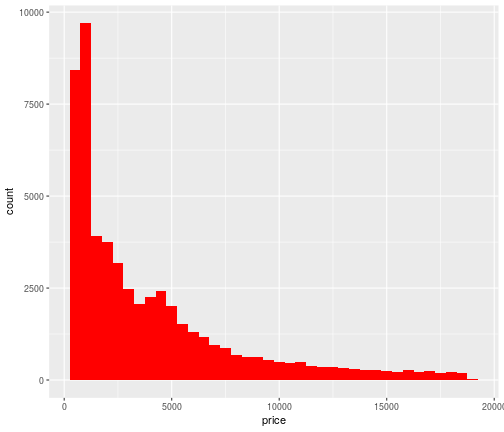
15
Change border color
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram(binwidth = 500,color='white', fill = 'blue')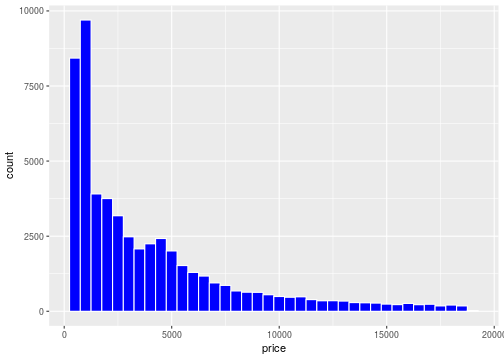
16
An aside on colour
17
Customise colour
- Many colours come built in to R.
18
Customise colour
- Many colours come built in to R.
- In some cases you may wish to select your own color.
18
Customise colour
- Many colours come built in to R.
- In some cases you may wish to select your own color.
- Customising colour requires appreciating how a computer understands color.
18
Customise colour
- Many colours come built in to R.
- In some cases you may wish to select your own color.
- Customising colour requires appreciating how a computer understands color.
- We will do this by looking at RGB hex codes.
18
Customise colour
- Many colours come built in to R.
- In some cases you may wish to select your own color.
- Customising colour requires appreciating how a computer understands color.
- We will do this by looking at RGB hex codes.
- Using this system, to a computer #ff0000 is red.
18
The RGB system
- One color model used by computers encodes every colour by the amount of red, green and blue light mixed to make that colour.
19
The RGB system
- One color model used by computers encodes every colour by the amount of red, green and blue light mixed to make that colour.
- This is called the RGB color model.
19
The RGB system
- One color model used by computers encodes every colour by the amount of red, green and blue light mixed to make that colour.
- This is called the RGB color model.
- A value between 0 and 255 indicates the strength of red, green and blue.
19
The RGB system
- One color model used by computers encodes every colour by the amount of red, green and blue light mixed to make that colour.
- This is called the RGB color model.
- A value between 0 and 255 indicates the strength of red, green and blue.
- These values between 0 and 255 are represented in two hexadecimal digits.
19
Hexadecimal
- In hexadecimal:
- a is ten,
- b is eleven,
- c is twelve...
- f is fifteen.
- Take the first digit and multiply by 16 and add the second digit
- Hexadecimal is used since each digit corresponds to 4 bits in computer memory.
20
Examples
- 10 in hexadecimal is 1×16+0=161×16+0=16 in decimal
- 1a in hexadecimal is 1×16+10=26 in decimal
- 2b in hexadecimal is 2×16+11=43 in decimal
- What is e4 in decimal?
21
Color picker
- One online tool to find the hex code of a color is here.
- Suppose we want to the histogram to be this brown color.
22
Color picker
- One online tool to find the hex code of a color is here.
- Suppose we want to the histogram to be this brown color.
- The hex code is #b35900 which is 179/256 red, 89/256 green and no blue.
22
Color picker
- One online tool to find the hex code of a color is here.
- Suppose we want to the histogram to be this brown color.
- The hex code is #b35900 which is 179/256 red, 89/256 green and no blue.
- This can be provided as a string, to the
fillorcolorargument ofgeom_histogram.
22
Brown histogram
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram(binwidth = 500,color='white', fill = '#b35900')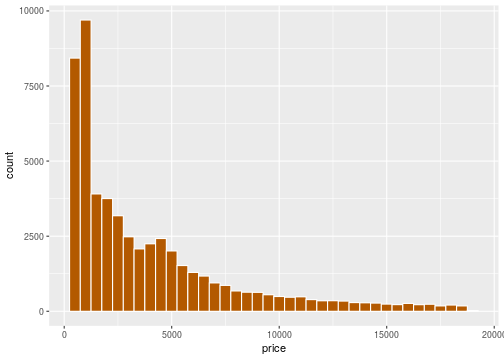
23
Finding hex codes
- It is useful to know hex codes since at times you may want to match colors for a specific purpose.
24
Finding hex codes
- It is useful to know hex codes since at times you may want to match colors for a specific purpose.
- For instance you may want the colors to match the brand colors of a client.
24
Finding hex codes
- It is useful to know hex codes since at times you may want to match colors for a specific purpose.
- For instance you may want the colors to match the brand colors of a client.
- For example a simple online search tells us that Coca Color red is #f40000
24
Finding hex codes
- It is useful to know hex codes since at times you may want to match colors for a specific purpose.
- For instance you may want the colors to match the brand colors of a client.
- For example a simple online search tells us that Coca Color red is #f40000
- The green color worn by NBA team the Milwaukee Bucks is #00471b.
24
Histograms (Bucks Colors)
ggplot(data = diamonds,mapping = aes(x=price))+ geom_histogram(fill='#00471b',color='#eee1c6')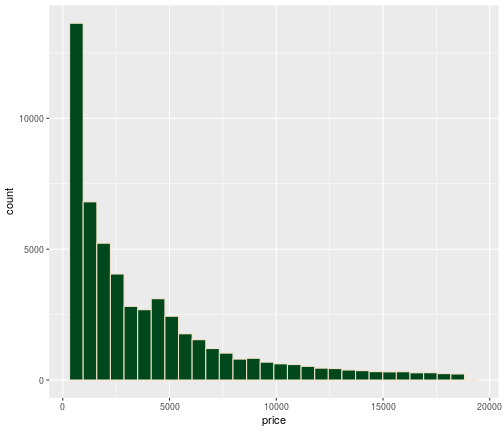
25
An exercise
- Find the hex codes for a color(s) associated with:
- A brand you like, or
- A sports team you like, or
- Your country's flag,
- Anything else
- Construct a histogram of the variable carat with these colors.
26
Density plot
27
Density
- For a smoother version of a histogram we can use a different geom called
geom_density.
28
Density
- For a smoother version of a histogram we can use a different geom called
geom_density. - This in fact computes a kernel density estimate of the variable.
28
Density
- For a smoother version of a histogram we can use a different geom called
geom_density. - This in fact computes a kernel density estimate of the variable.
- The level of smoothness is controlled by a bandwidth parameter
28
Density
- For a smoother version of a histogram we can use a different geom called
geom_density. - This in fact computes a kernel density estimate of the variable.
- The level of smoothness is controlled by a bandwidth parameter
- All the computation is done by
ggplot2.
28
Density plot
ggplot(data = diamonds,mapping = aes(x=price))+ geom_density()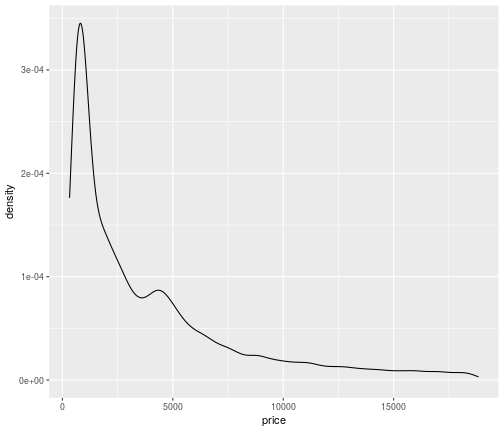
29
Density plot (thicker)
ggplot(data = diamonds,mapping = aes(x=price))+ geom_density(size=3)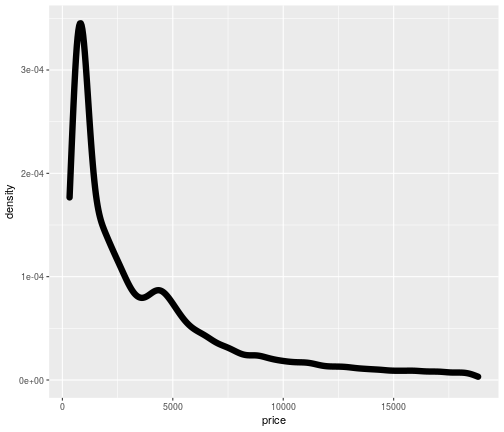
30
How is density calculated?
- The kernel density estimate is a popular nonparametric technique that estimates a density as
ˆf(x)=1nn∑i=1Kh(x−xi)
- Here, Kh() is a kernel function that depends on a bandwidth h.
31
Uniform kernel
- The simplest kernel function is the uniform kernel
- Kh(u)=1/h if |u|<h
- Kh(u)=0 otherwise
32
Uniform kernel
- The simplest kernel function is the uniform kernel
- Kh(u)=1/h if |u|<h
- Kh(u)=0 otherwise
- At a point x, the estimated density is proportional to the number of points that are close to x.
32
Uniform kernel
- The simplest kernel function is the uniform kernel
- Kh(u)=1/h if |u|<h
- Kh(u)=0 otherwise
- At a point x, the estimated density is proportional to the number of points that are close to x.
- By close, we mean within h units of x.
32
Extremes
- If the bandwidth gets extremely large then for any x, all sample points are considered close.
33
Extremes
- If the bandwidth gets extremely large then for any x, all sample points are considered close.
- The formula for the kernel density becomes a flat line.
33
Extremes
- If the bandwidth gets extremely large then for any x, all sample points are considered close.
- The formula for the kernel density becomes a flat line.
- If the bandwidth gets extremely small then for any x we choose, the density is just the number of points in the sample equal to x.
33
Extremes
- If the bandwidth gets extremely large then for any x, all sample points are considered close.
- The formula for the kernel density becomes a flat line.
- If the bandwidth gets extremely small then for any x we choose, the density is just the number of points in the sample equal to x.
- The kernel density is made up of spikes at the sample points.
33
Defaults
- By default,
geom_density- Uses a Gaussian kernel
- Selects the bandwidth using Silverman's rule of thumb
34
Defaults
- By default,
geom_density- Uses a Gaussian kernel
- Selects the bandwidth using Silverman's rule of thumb
- The same principles apply:
- Large bandwidth leads to more smoothness
- Small bandwidth leads to more bumpiness
34
Density plot: Low bandwidth
ggplot(data = diamonds,mapping = aes(x=price))+ geom_density(bw=100)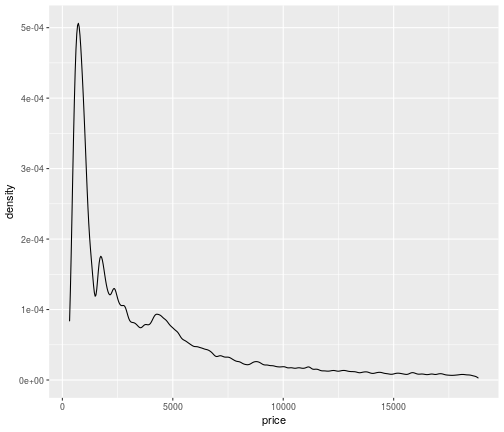
35
Density plot: High bandwidth
ggplot(data = diamonds,mapping = aes(x=price))+ geom_density(bw=2000)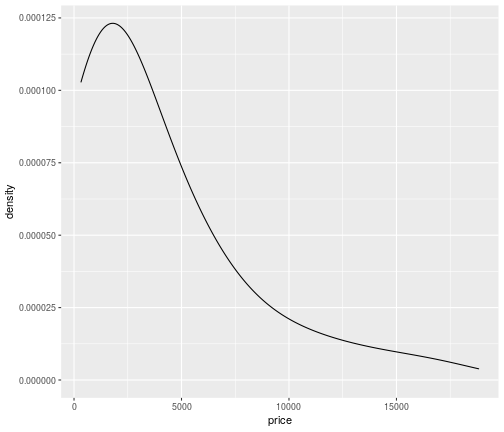
36
Density plot: Low bandwidth
ggplot(data = diamonds,mapping = aes(x=price))+ geom_density(bw=0.0001)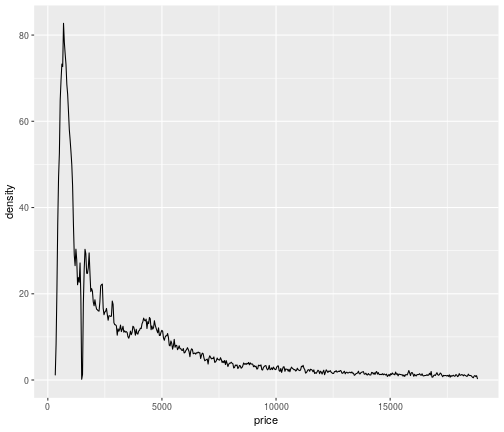
37
Density plot: High bandwidth
ggplot(data = diamonds,mapping = aes(x=price))+ geom_density(bw=80000)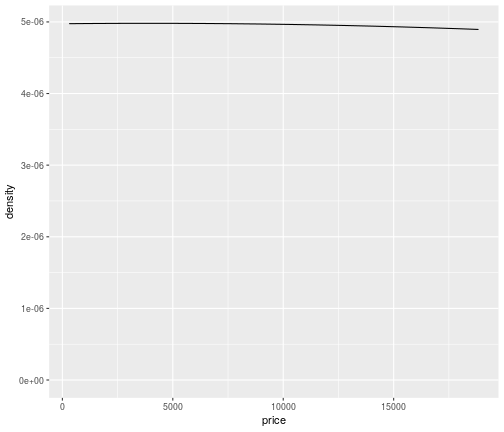
38
Summary
- With both histograms and density plots
- If the bin width or bandwidth is too small the plot may look bumpy. This can exaggerate features that are not significant.
- If the bin width or bandwidth is too large the plot may smooth over important features like local modes.
- Always try a few different values of bin width or bandwidth.
39
Finding outliers
40
Outliers
- Histograms and density plots give a good idea of shape and local modes.
41
Outliers
- Histograms and density plots give a good idea of shape and local modes.
- Sometimes they can obscure outliers.
41
Outliers
- Histograms and density plots give a good idea of shape and local modes.
- Sometimes they can obscure outliers.
- For finding outliers a rug plot can be useful
41
Outliers
- Histograms and density plots give a good idea of shape and local modes.
- Sometimes they can obscure outliers.
- For finding outliers a rug plot can be useful
- For finding outliers while still getting a good idea of skew, boxplots can be useful.
41
Outliers
- Histograms and density plots give a good idea of shape and local modes.
- Sometimes they can obscure outliers.
- For finding outliers a rug plot can be useful
- For finding outliers while still getting a good idea of skew, boxplots can be useful.
- We can investigate using the variable carat
41
Carat: Histogram
ggplot(data = diamonds,mapping = aes(x=carat))+ geom_histogram()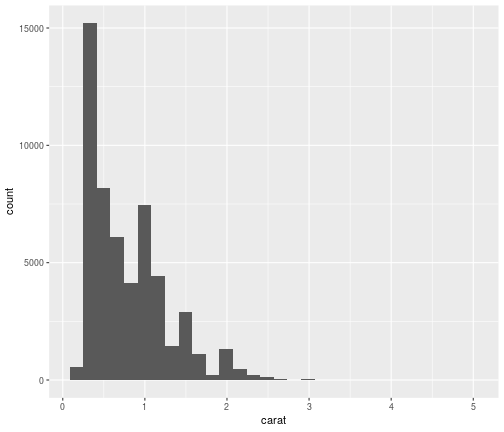
42
Carat: Rug plot
ggplot(data = diamonds,mapping = aes(x=carat))+ geom_rug()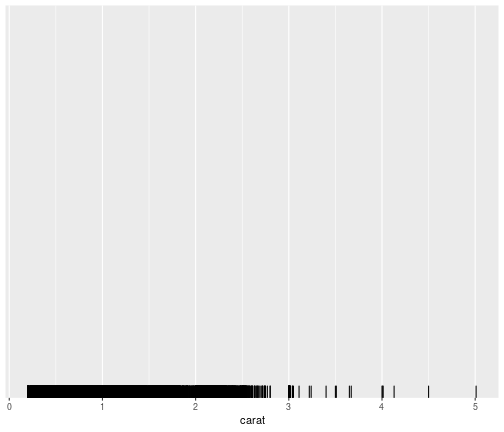
43
Box plot
- The box plot summarises 5 numbers
- Median
- First quartile Q1
- Third quartile Q3
- Upper Fence U=Q3+1.5×(Q3−Q1)
- Lower Fence L=Q1−1.5×(Q3−Q1)
- Anything lying outside the fences represented as dots.
- When no points lie outside the fence, the fence is set to the maximum or minimum.
44
Carat: Boxplot
ggplot(data = diamonds,mapping = aes(y=carat))+ geom_boxplot()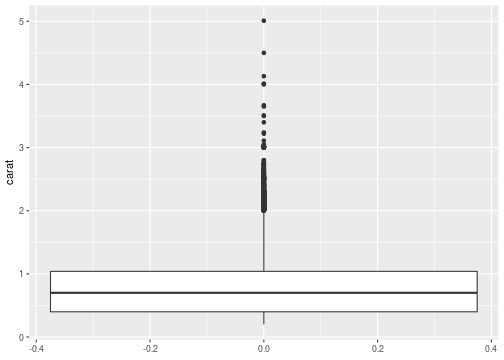
45
Change of aesthetic
- Notice that the aesthetic changed!
46
Change of aesthetic
- Notice that the aesthetic changed!
- In the boxplot, the value of the variable is represented by the vertical (or y axis).
46
Change of aesthetic
- Notice that the aesthetic changed!
- In the boxplot, the value of the variable is represented by the vertical (or y axis).
- We can change the definition of the upper and lower fence by passing the
coefargument togeom_boxplot.
46
Change of aesthetic
- Notice that the aesthetic changed!
- In the boxplot, the value of the variable is represented by the vertical (or y axis).
- We can change the definition of the upper and lower fence by passing the
coefargument togeom_boxplot. - This changes the 1.5 used in calculating the fence to whatever you specify
46
Changing fences
ggplot(data = diamonds,mapping = aes(y=carat))+ geom_boxplot(coef=4)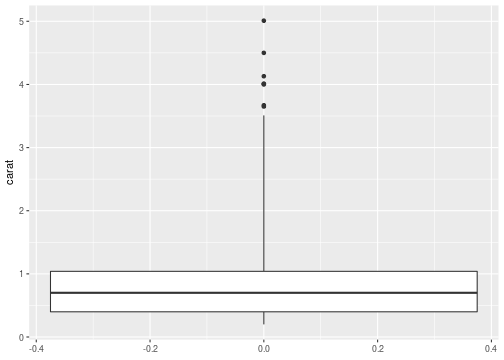
47
Notches
- Notches can be added to a boxplot
48
Notches
- Notches can be added to a boxplot
- These are set to 1.58×(Q3−Q1)√n
48
Notches
- Notches can be added to a boxplot
- These are set to 1.58×(Q3−Q1)√n
- This roughly gives a 95% confidence interval for the median.
48
Notches
- Notches can be added to a boxplot
- These are set to 1.58×(Q3−Q1)√n
- This roughly gives a 95% confidence interval for the median.
- We will use a smaller dataset on the mileage of cars for this example to clearly illustrate the notches.
48
Notches
ggplot(data = mpg,mapping = aes(y=cty))+ geom_boxplot(notch = T)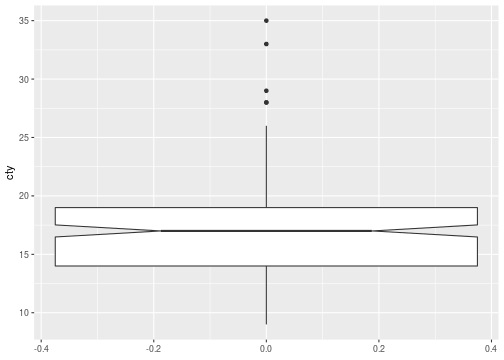
49
One Non-Metric Variable
50
Nominal v Ordinal
- Non-metric variables are made up of nominal and ordinal variables.
51
Nominal v Ordinal
- Non-metric variables are made up of nominal and ordinal variables.
- Nominal variables have no ordering in the categories of data:
- Manufacturer of car (Audi, Toyota, etc).
51
Nominal v Ordinal
- Non-metric variables are made up of nominal and ordinal variables.
- Nominal variables have no ordering in the categories of data:
- Manufacturer of car (Audi, Toyota, etc).
- Ordinal variables do have an ordering in the categories:
- Quality of diamonds (Fair, Good, etc).
51
Non-metric variables in R
- Non-metric variables can be stored in R as
- Character variables (nominal data)
- Factors (nominal data)
- Ordered factors (ordinal data)
- You can check with the
strfunction
52
Diamonds data
str(diamonds)## tibble [53,940 × 10] (S3: tbl_df/tbl/data.frame)## $ carat : num [1:53940] 0.23 0.21 0.23 0.29 0.31 0.24 0.24 0.26 0.22 0.23 ...## $ cut : Ord.factor w/ 5 levels "Fair"<"Good"<..: 5 4 2 4 2 3 3 3 1 3 ...## $ color : Ord.factor w/ 7 levels "D"<"E"<"F"<"G"<..: 2 2 2 6 7 7 6 5 2 5 ...## $ clarity: Ord.factor w/ 8 levels "I1"<"SI2"<"SI1"<..: 2 3 5 4 2 6 7 3 4 5 ...## $ depth : num [1:53940] 61.5 59.8 56.9 62.4 63.3 62.8 62.3 61.9 65.1 59.4 ...## $ table : num [1:53940] 55 61 65 58 58 57 57 55 61 61 ...## $ price : int [1:53940] 326 326 327 334 335 336 336 337 337 338 ...## $ x : num [1:53940] 3.95 3.89 4.05 4.2 4.34 3.94 3.95 4.07 3.87 4 ...## $ y : num [1:53940] 3.98 3.84 4.07 4.23 4.35 3.96 3.98 4.11 3.78 4.05 ...## $ z : num [1:53940] 2.43 2.31 2.31 2.63 2.75 2.48 2.47 2.53 2.49 2.39 ...53
Mpg data
str(mpg)## tibble [234 × 11] (S3: tbl_df/tbl/data.frame)## $ manufacturer: chr [1:234] "audi" "audi" "audi" "audi" ...## $ model : chr [1:234] "a4" "a4" "a4" "a4" ...## $ displ : num [1:234] 1.8 1.8 2 2 2.8 2.8 3.1 1.8 1.8 2 ...## $ year : int [1:234] 1999 1999 2008 2008 1999 1999 2008 1999 1999 2008 ...## $ cyl : int [1:234] 4 4 4 4 6 6 6 4 4 4 ...## $ trans : chr [1:234] "auto(l5)" "manual(m5)" "manual(m6)" "auto(av)" ...## $ drv : chr [1:234] "f" "f" "f" "f" ...## $ cty : int [1:234] 18 21 20 21 16 18 18 18 16 20 ...## $ hwy : int [1:234] 29 29 31 30 26 26 27 26 25 28 ...## $ fl : chr [1:234] "p" "p" "p" "p" ...## $ class : chr [1:234] "compact" "compact" "compact" "compact" ...54
Bar plot
- A common plot for non-metric data is the bar plot for the frequency of observations for each level of the factor.
55
Bar plot
- A common plot for non-metric data is the bar plot for the frequency of observations for each level of the factor.
- The height of each bar indicates the number of observations in a particular category.
55
Bar plot
- A common plot for non-metric data is the bar plot for the frequency of observations for each level of the factor.
- The height of each bar indicates the number of observations in a particular category.
- This can be done using
geom_bar
55
Bar plot
ggplot(data = diamonds, mapping = aes(x=cut))+ geom_bar()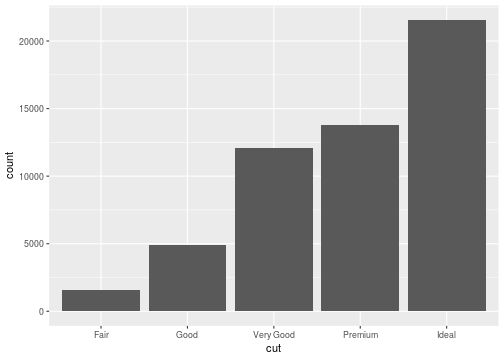
56
Bar plot
ggplot(data = mpg, mapping = aes(x=manufacturer))+ geom_bar()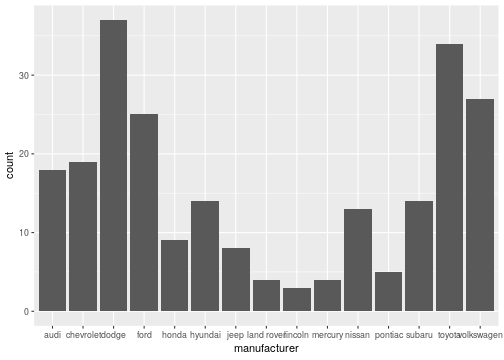
57
Two Continuous Variables
58
What to look for
- Outliers
59
What to look for
- Outliers
- Dependence or correlation
59
What to look for
- Outliers
- Dependence or correlation
- Remember that correlation does not imply causation!
59
What to look for
- Outliers
- Dependence or correlation
- Remember that correlation does not imply causation!
- Non linear relationships.
59
Scatter plot
- For two metric variables use a scatter plot
- One variable is represented by the
xaesthetic - The other is represented by the
yaesthetic - The geometry we use is
geom_point.
- One variable is represented by the
- We will continue to use the
diamondsdataset
60
Scatterplot
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+geom_point()
61
Overplotting
- When using big datasets, sometimes the points cover one another or are too close.
62
Overplotting
- When using big datasets, sometimes the points cover one another or are too close.
- This is sometimes called overplotting.
62
Overplotting
- When using big datasets, sometimes the points cover one another or are too close.
- This is sometimes called overplotting.
- Some solutions:
- Try smaller points (size)
- Try more transparent points (alpha)
- Try a different geom
62
Changing size
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+ geom_point(size=0.1)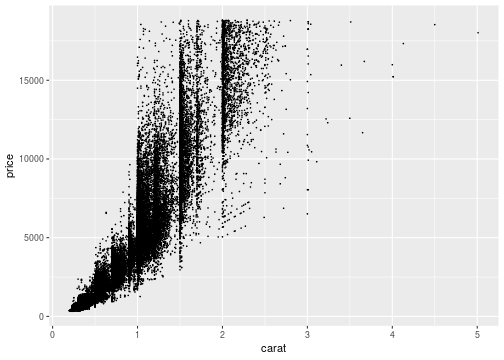
63
Changing alpha
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+ geom_point(alpha=0.2)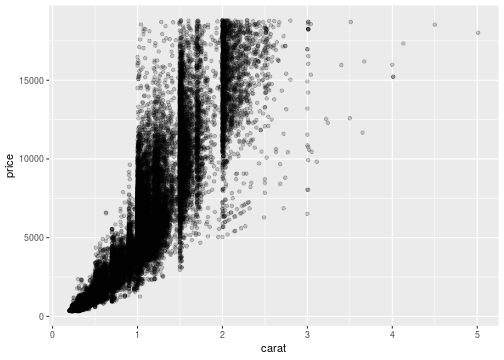
64
Changing geom
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+ geom_bin2d()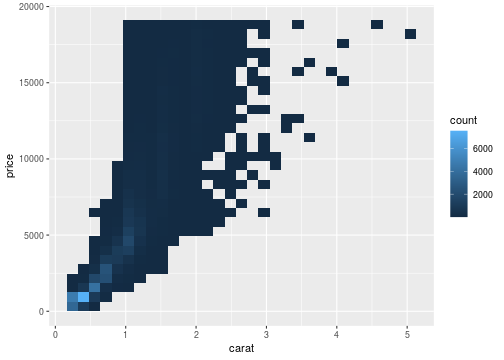
65
Hexagonal bins
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+ geom_hex()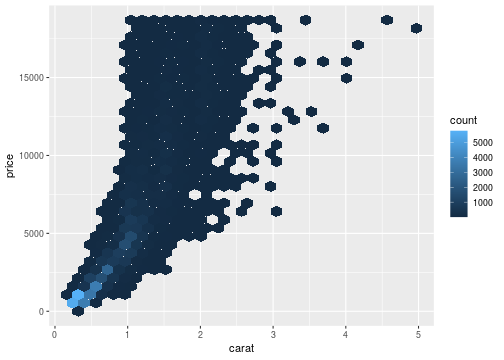
66
Changing geom
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+ geom_density2d()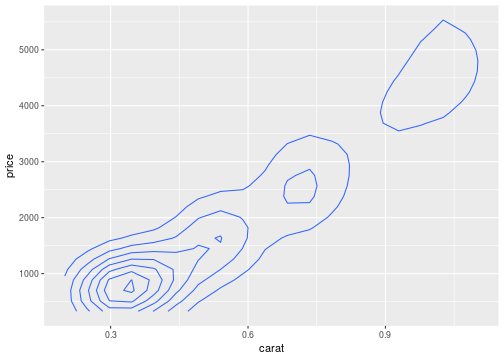
67
Time series plots
- When the x variable is time, it often makes more sense to join dots with a line.
68
Time series plots
- When the x variable is time, it often makes more sense to join dots with a line.
- This way we can see
- Trend
- Seasonality
- Outliers
- Structural break
68
Economics dataset
- We will use the economics dataset (comes with ggplot2)
str(economics)## tibble [574 × 6] (S3: spec_tbl_df/tbl_df/tbl/data.frame)## $ date : Date[1:574], format: "1967-07-01" "1967-08-01" ...## $ pce : num [1:574] 507 510 516 512 517 ...## $ pop : num [1:574] 198712 198911 199113 199311 199498 ...## $ psavert : num [1:574] 12.6 12.6 11.9 12.9 12.8 11.8 11.7 12.3 11.7 12.3 ...## $ uempmed : num [1:574] 4.5 4.7 4.6 4.9 4.7 4.8 5.1 4.5 4.1 4.6 ...## $ unemploy: num [1:574] 2944 2945 2958 3143 3066 ...- Notice date is its own type of variable
69
Unemployed persons
ggplot(economics, aes(x=date, y=unemploy))+ geom_line()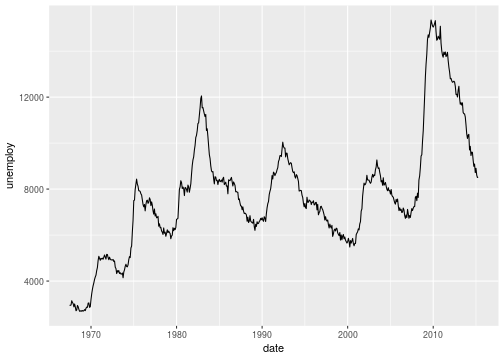
70
An aside on log scales
71
Scale
- For variables that are heavily skewed it can be better to look at a log scale.
72
Scale
- For variables that are heavily skewed it can be better to look at a log scale.
- For a regular scale you add as you move up the scale.
72
Scale
- For variables that are heavily skewed it can be better to look at a log scale.
- For a regular scale you add as you move up the scale.
- For a log scale you multiply as you move up the scale.
72
Scale
- For variables that are heavily skewed it can be better to look at a log scale.
- For a regular scale you add as you move up the scale.
- For a log scale you multiply as you move up the scale.
- The log scale has the effect of putting more distance between smaller values and compressing higher values.
72
Regular scale
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+ geom_point()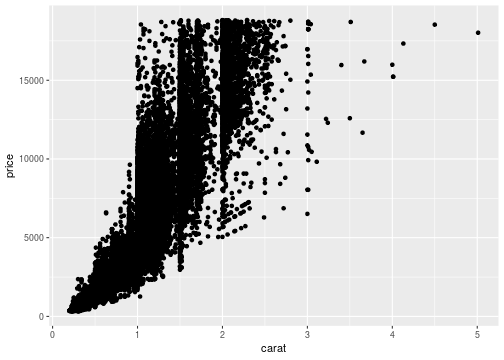
73
Log scale
ggplot(data = diamonds, mapping = aes(x=carat,y=price))+ geom_point()+scale_x_log10()+scale_y_log10()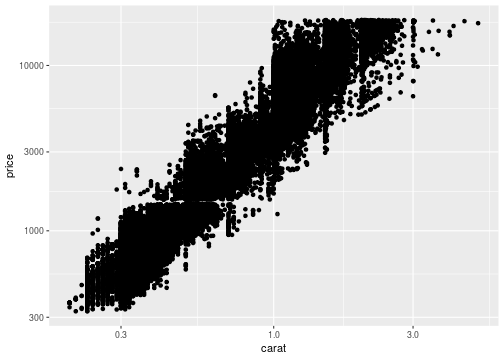
74
Zipf's Law
- In text mining, a well known empirical result is that the occurence of words in a document often follows Zipf's law
Prob(r)=r−sK
- Here r is the rank of the word (1 is the most frequent, N the least frequent).
- K=N∑x=1x−s is constant with respect to r.
75
Three documents
- We will look at three documents:
- The Australian Constitution
- The script of Avengers Endgame
- The homepage of online retailer Tao Bao.
76
Australian Constitution
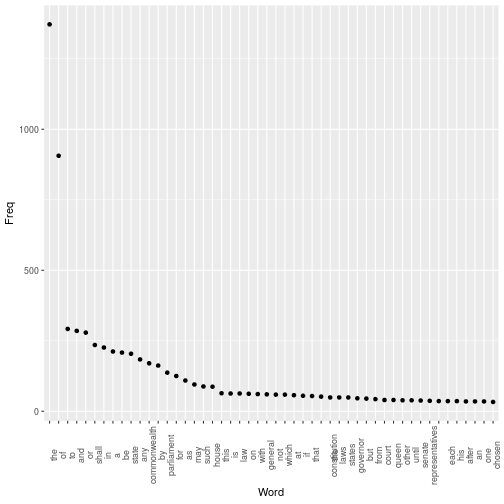
77
Australian Constitution
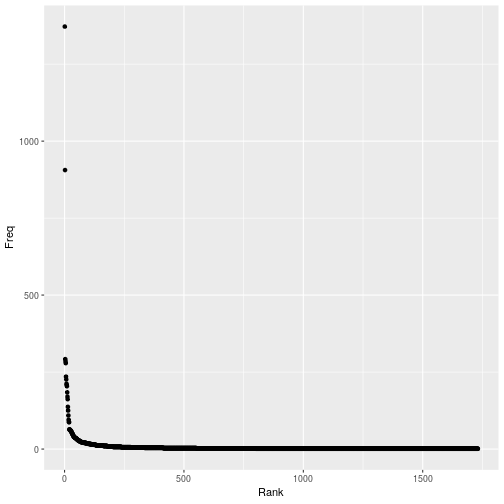
78
Zipf Law
- Zipf's law predicts that
Pr(r)≈r−s/K
- Taking logs on both sides
log(f(r))≈−slog(r)−log(K)
- Look at the plot on the log scale.
79
Australian Constitution
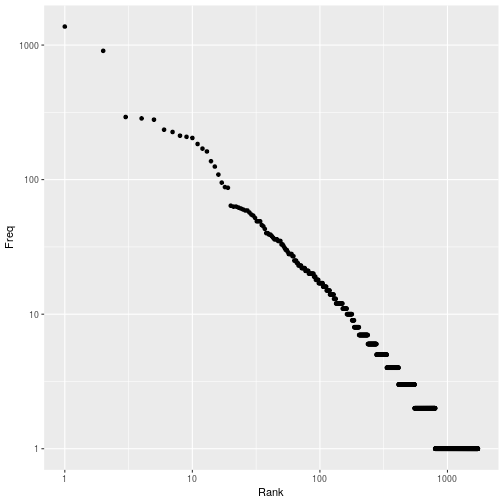
80
Avengers Endgame
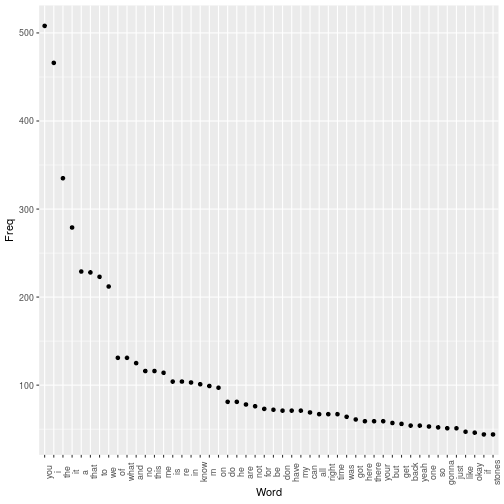
81
Avengers Endgame
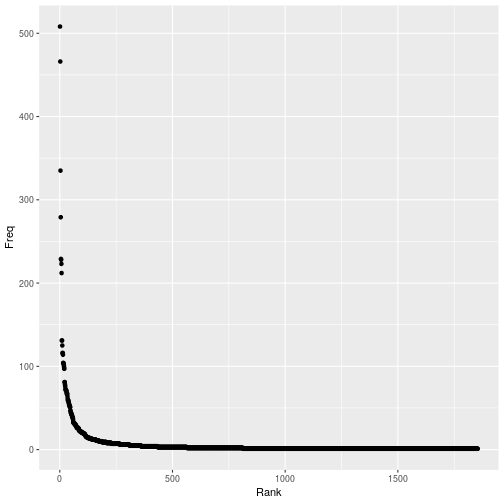
82
Avengers Endgame
83
Tao Bao
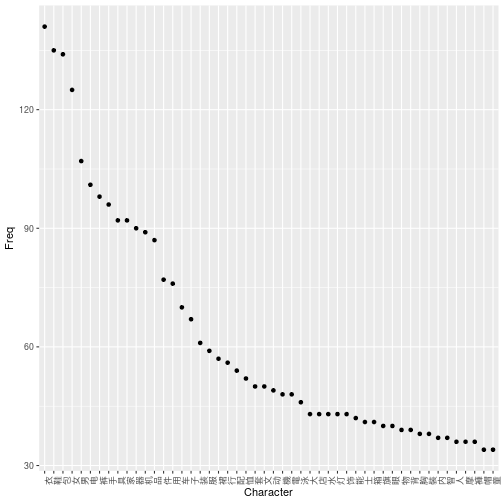
84
Tao Bao
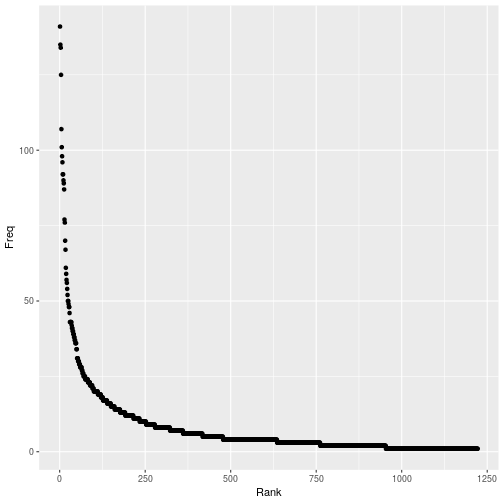
85
Tao Bao
86
Other applications
- A similar observation is also made for the size of companies.
- Gibrat's Law claims that the growth rate of a company is independent of its size.
- This implies that the distribution of company size will be similar to the distribution of word frequency.
- Gibrat's law has also been applied to city populations.
87
Metric and Non-Metric Data
88
Side by side plots
- When one variable is metric and the other non-metric we can easily put plots next to one another side by side.
- Simply map the non-metric variable to the x aesthetic and the metric variable to the y aesthetic.
89
Boxplots
ggplot(data = diamonds, mapping = aes(x=cut,y=price))+ geom_boxplot()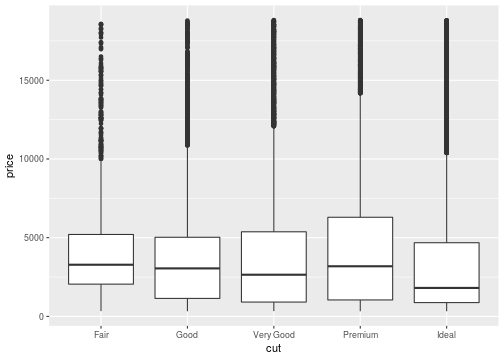
90
Change axes
ggplot(data = diamonds, mapping = aes(x=price,y=cut))+ geom_boxplot()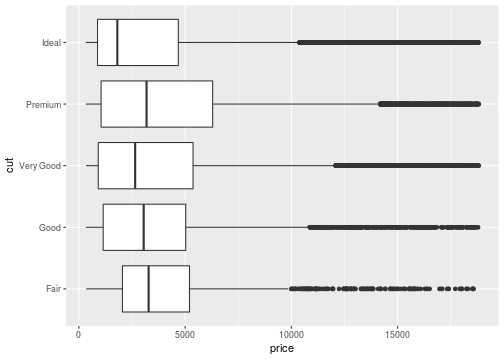
91
With notches
- Recall that the notches provide a confidence interval around the median.
92
With notches
- Recall that the notches provide a confidence interval around the median.
- These are particularly useful when comparing boxplots to one another.
92
With notches
- Recall that the notches provide a confidence interval around the median.
- These are particularly useful when comparing boxplots to one another.
- In general, if the confidence intervals overlap then the medians are not signficantly different.
92
With notches
- Recall that the notches provide a confidence interval around the median.
- These are particularly useful when comparing boxplots to one another.
- In general, if the confidence intervals overlap then the medians are not signficantly different.
- This is NOT a formal test, but still gives a useful indication.
92
Boxplots (no overlap)
ggplot(data = mpg, mapping = aes(x=drv,y=hwy))+ geom_boxplot(notch=T)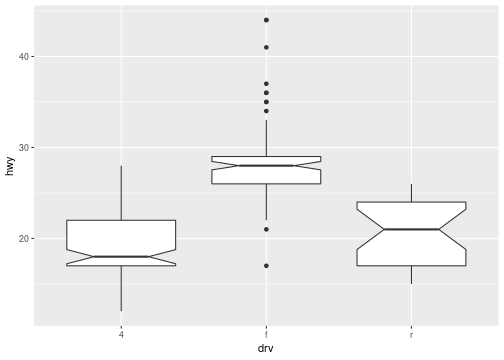
93
Boxplots (some overlap)
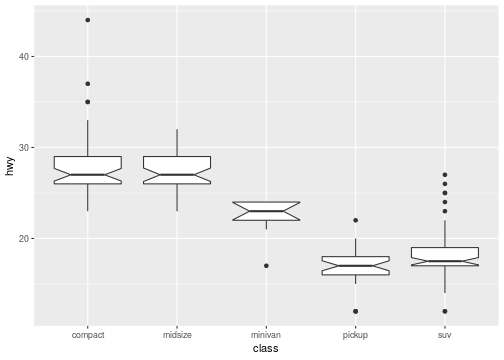
94
Violin plot
- A violin plot is a newer visualisation.
- A kernel density is mirrored then arranged vertically.
- Specify the same way but use geom_violin
95
Violin plot
ggplot(data = diamonds, mapping = aes(x=cut,y=price))+ geom_violin()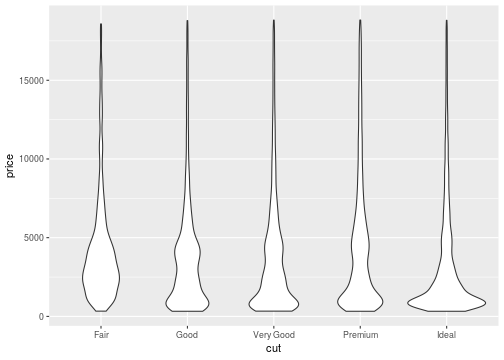
96
Violin plot
ggplot(data = diamonds, mapping = aes(x=cut,y=price))+ geom_violin()+coord_flip()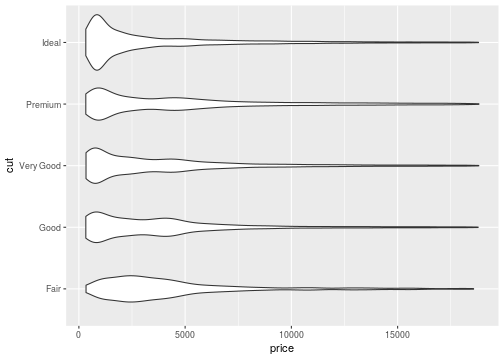
97
Jittering
- A scatter plot can be used for non-metric data but can easily suffer from overplotting (one point on another).
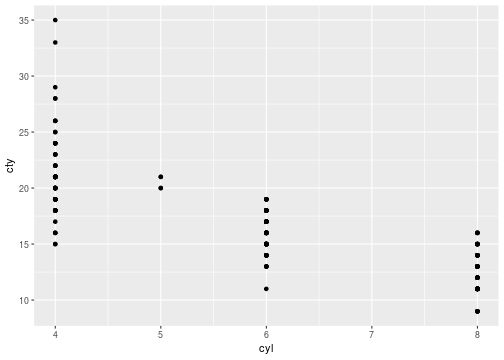
98
Jittering
- Add random noise by jittering
ggplot(data = mpg, mapping = aes(x=cyl,y=cty))+ geom_point(position = 'jitter')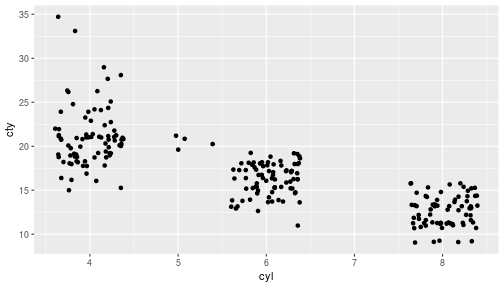
99