Predictive Analytics
Data Visualisation and Analytics
Anastasios Panagiotelis and Lauren Kennedy
Lecture 8
1
Time for Analytics
2
Minor adjustments
- So far our attention has completely been on visualisation.
3
Minor adjustments
- So far our attention has completely been on visualisation.
- For the remainder of the unit we will focus on analytics
3
Minor adjustments
- So far our attention has completely been on visualisation.
- For the remainder of the unit we will focus on analytics
- In particular our focus will be on making predictions.
3
Textbook
- Much of the content of these slides is covered in Introduction to Statistical Learning by James, Witten Hastie, and Tibshirani.
4
Textbook
- Much of the content of these slides is covered in Introduction to Statistical Learning by James, Witten Hastie, and Tibshirani.
- In particular Chapters 2, 4 and 8.
4
Textbook
- Much of the content of these slides is covered in Introduction to Statistical Learning by James, Witten Hastie, and Tibshirani.
- In particular Chapters 2, 4 and 8.
- The textbook is not mandatory but you may find it useful.
4
Textbook
- Much of the content of these slides is covered in Introduction to Statistical Learning by James, Witten Hastie, and Tibshirani.
- In particular Chapters 2, 4 and 8.
- The textbook is not mandatory but you may find it useful.
- It is available for free.
4
Prediction
- Prediction arises in many business contexts.
5
Prediction
- Prediction arises in many business contexts.
- There is some unknown variable that is the target of the prediction.
- This is usually denoted y and may be called the dependent variable, or response or target variable.
5
Prediction
- Prediction arises in many business contexts.
- There is some unknown variable that is the target of the prediction.
- This is usually denoted y and may be called the dependent variable, or response or target variable.
- There are some known variables that are used to make the prediction.
- These are usually denoted x and may be called the independent variables, or predictors or features.
5
Supervised Learning
- For some observations data will be available for both y AND x.
6
Supervised Learning
- For some observations data will be available for both y AND x.
- We can use these observations to learn some rule that gives predictions of y as a function of x.
6
Supervised Learning
- For some observations data will be available for both y AND x.
- We can use these observations to learn some rule that gives predictions of y as a function of x.
- This prediction is denoted ^y=^f(x)
6
Supervised Learning
- For some observations data will be available for both y AND x.
- We can use these observations to learn some rule that gives predictions of y as a function of x.
- This prediction is denoted ^y=^f(x)
- This general setup is often called supervised learning.
6
Summary
| Variable | Training | Evaluation |
|---|---|---|
| Predictor 1 (X1) | Data available | Data available |
| Predictor 2 (X2) | Data available | Data available |
| Dependent Variable (Y) | Data available | Data NOT available |
7
Example
| Variable | Old Customers | New Customer |
|---|---|---|
| Age (X1) | Data available | Data available |
| Limit (X2) | Data available | Data available |
| Default (Y) | Data available | Data NOT available |
8
Regression
- Sometimes y is a numeric (metric) variable. For example
- Company profit next month.
- Amount spent by a customer.
- Demand for a new product.
9
Regression
- Sometimes y is a numeric (metric) variable. For example
- Company profit next month.
- Amount spent by a customer.
- Demand for a new product.
- In this case we are doing regression.
9
Regression
- Sometimes y is a numeric (metric) variable. For example
- Company profit next month.
- Amount spent by a customer.
- Demand for a new product.
- In this case we are doing regression.
- This can be more general than the linear regression that you may be familiar with.
9
Classification
- Sometimes y is a categorical (nominal, non-metric) variable. For example
- Will a borrower default on a loan?
- Can we detect which tax returns are fraudulent?
- Can we predict which brand customers will choose?
10
Classification
- Sometimes y is a categorical (nominal, non-metric) variable. For example
- Will a borrower default on a loan?
- Can we detect which tax returns are fraudulent?
- Can we predict which brand customers will choose?
- In this case we are doing classification.
10
Credit Data
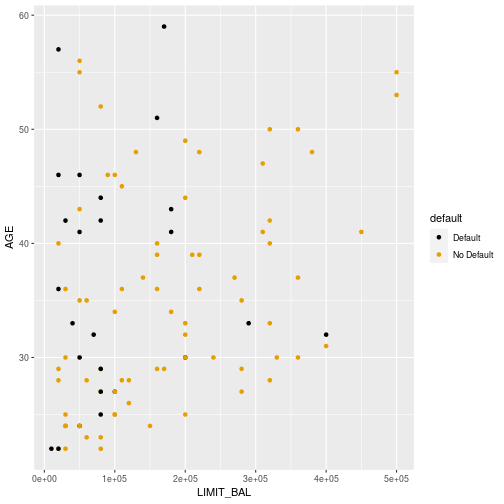
11
Default or not?
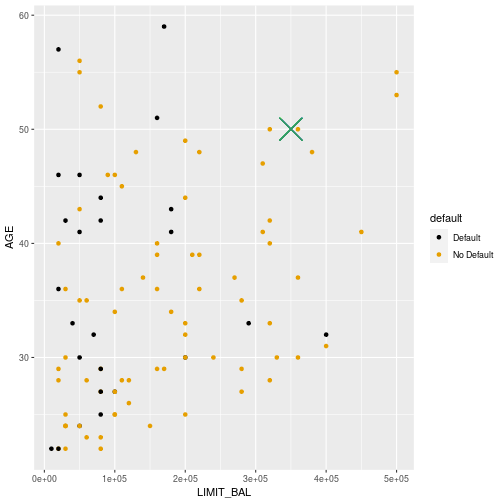
12
Default or not?
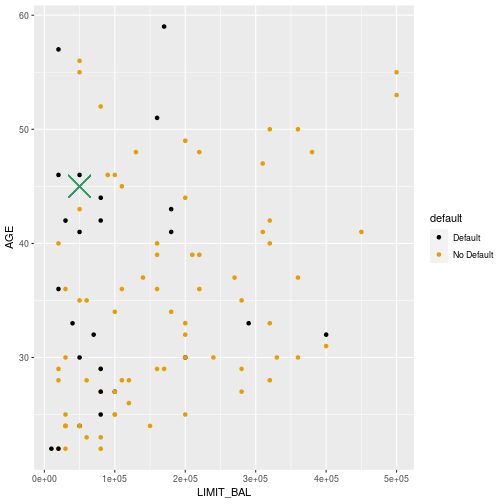
13
Assessing Classification
14
Some math
- Generally data yi and xi available for i=1,2,3,…,n.
15
Some math
- Generally data yi and xi available for i=1,2,3,…,n.
- An algorithm is trained on this data. Some function of xi is derived where ^y=^f(x).
15
Some math
- Generally data yi and xi available for i=1,2,3,…,n.
- An algorithm is trained on this data. Some function of xi is derived where ^y=^f(x).
- How to decide if ^f is a good classifier or bad classifier?
15
Misclassification
- The misclassification error is given by
1nn∑i=1I(yi≠^yi)
- Here I(.) equals 1 of the statement in parentheses is true and 0 otherwise.
16
Misclassification
- The misclassification error is given by
1nn∑i=1I(yi≠^yi)
- Here I(.) equals 1 of the statement in parentheses is true and 0 otherwise.
- Large numbers imply a worse performance.
16
Misclassification
- The misclassification error is given by
1nn∑i=1I(yi≠^yi)
- Here I(.) equals 1 of the statement in parentheses is true and 0 otherwise.
- Large numbers imply a worse performance.
- Since all n points are used for training and evaluation this measures in-sample performance.
16
Training v Test
- In practice we want predictions for values of y that are not yet observed.
17
Training v Test
- In practice we want predictions for values of y that are not yet observed.
- To artificially create this scenario the data we have available can be split into two
- Training sample used to determing ^f
- Test sample used to evaluate ^f.
17
Training v Test
- In practice we want predictions for values of y that are not yet observed.
- To artificially create this scenario the data we have available can be split into two
- Training sample used to determing ^f
- Test sample used to evaluate ^f.
- The y values of the test sample will be treated as unknown during training.
17
Notation
- N1 is the set of indices for training data.
- |N1| is the number of observations in training data.
- N0 is the set of indices for test data
- |N0| is the number of observations in test data.
18
Example
- Suppose there are five observations, (y1,x1),(y2,x2),…,(y5,x5)
- Suppose observations 1,2 and 4 are used as training data.
- Suppose observations 3 and 5 are used as test data.
- Then N1={1,2,4} and |N1|=3
- And N0={3,5} and |N0|=2
- Only the data in N1 is used to determine ^f
19
Training v Test
Training error rate
1|N1|∑i∈N1I(yi≠^yi)
Test error rate
1|N0|∑i∈N0I(yi≠^yi)
20
Overfitting
- Some methods perform very well (even perfectly) on training error rate.
21
Overfitting
- Some methods perform very well (even perfectly) on training error rate.
- Usually these same methods will perform poorly on test error rate.
21
Overfitting
- Some methods perform very well (even perfectly) on training error rate.
- Usually these same methods will perform poorly on test error rate.
- This phenomenon is called overfitting.
21
Overfitting
- Some methods perform very well (even perfectly) on training error rate.
- Usually these same methods will perform poorly on test error rate.
- This phenomenon is called overfitting.
- Generally achieving a low test error rate (also called out-of-sample or generalisation error) is more important.
21
A simple example
- Consider a test set of a single observation N0={j}.
22
A simple example
- Consider a test set of a single observation N0={j}.
- The classifier is trained using all data apart from j.
22
A simple example
- Consider a test set of a single observation N0={j}.
- The classifier is trained using all data apart from j.
- This classifier is then used to predict the value of yj.
22
A simple example
- Consider a test set of a single observation N0={j}.
- The classifier is trained using all data apart from j.
- This classifier is then used to predict the value of yj.
- The choice of j may seem arbitrary.
22
Cross validation
- The process can be repeated so that each observation is left out exactly once.
23
Cross validation
- The process can be repeated so that each observation is left out exactly once.
- Each time all remaining observations are used as the training set.
23
Cross validation
- The process can be repeated so that each observation is left out exactly once.
- Each time all remaining observations are used as the training set.
- This process is called Leave-one-out cross validation(LOOCV)
23
k-fold CV
- A faster alternative to LOOCV is k-fold cross validation
24
k-fold CV
- A faster alternative to LOOCV is k-fold cross validation
- The data are randomly split into k partitions.
24
k-fold CV
- A faster alternative to LOOCV is k-fold cross validation
- The data are randomly split into k partitions.
- Each observation appears in exactly one partition, i.e. the partitions are non-overlapping.
24
k-fold CV
- A faster alternative to LOOCV is k-fold cross validation
- The data are randomly split into k partitions.
- Each observation appears in exactly one partition, i.e. the partitions are non-overlapping.
- Each partition is used as the test set exactly once.
24
For regression
- In regression rather than looking at the error rate it may be better to look at sums of squared errors.
25
For regression
- In regression rather than looking at the error rate it may be better to look at sums of squared errors.
- The concepts of test and training set can be used.
25
For regression
- In regression rather than looking at the error rate it may be better to look at sums of squared errors.
- The concepts of test and training set can be used.
- Leave one out cross validation and k-fold cross validation can be used in the same way.
25
Next step
- Eventually we will introduce specific algorithms for doing classification.
26
Next step
- Eventually we will introduce specific algorithms for doing classification.
- However for all these algorithms the distinction between training and test data is important.
26
Next step
- Eventually we will introduce specific algorithms for doing classification.
- However for all these algorithms the distinction between training and test data is important.
- Equally cross validation will consistently be used.
26
Next step
- Eventually we will introduce specific algorithms for doing classification.
- However for all these algorithms the distinction between training and test data is important.
- Equally cross validation will consistently be used.
- Make sure you understand how these ideas work, separately from specific algorithms.
26
Additional issues with prediction
27
Predict v Explain
- In this unit our emphasis will be on prediction.
28
Predict v Explain
- In this unit our emphasis will be on prediction.
- This is very different to explanation or causality.
28
Predict v Explain
- In this unit our emphasis will be on prediction.
- This is very different to explanation or causality.
- Consider the example of predicting sales of a Toyota by looking at number of internet searches for "Toyota".
28
Predict v Explain
- In this unit our emphasis will be on prediction.
- This is very different to explanation or causality.
- Consider the example of predicting sales of a Toyota by looking at number of internet searches for "Toyota".
- If there is a large number of people searching for "Toyota" it is more likely for sales of Toyota in the following period to be higher.
28
Causality
- This relationship is not easy to manipulate.
29
Causality
- This relationship is not easy to manipulate.
- For instance, if Toyota instructs its employees to spend the afternoon searching the word "Toyota" on Google, sales will not go up.
29
Causality
- This relationship is not easy to manipulate.
- For instance, if Toyota instructs its employees to spend the afternoon searching the word "Toyota" on Google, sales will not go up.
- In this case there is a common cause for browsing for cars and buying cars; namely the intent to buy cars.
29
Causality
- This relationship is not easy to manipulate.
- For instance, if Toyota instructs its employees to spend the afternoon searching the word "Toyota" on Google, sales will not go up.
- In this case there is a common cause for browsing for cars and buying cars; namely the intent to buy cars.
- Unlike intent to buy a car, browsing behaviour is observable and can be used for prediction.
29
Two class v Multiclass
- Many classification problems involve a y variable that can take two values.
- Default on credit card v Not Default
30
Two class v Multiclass
- Many classification problems involve a y variable that can take two values.
- Default on credit card v Not Default
- In other cases the y variable can take multiple values
- Brand choice, e.g. for instance Gucci v Louis Vuitton v YSL v Givenchy.
30
Two class v Multiclass
- Many classification problems involve a y variable that can take two values.
- Default on credit card v Not Default
- In other cases the y variable can take multiple values
- Brand choice, e.g. for instance Gucci v Louis Vuitton v YSL v Givenchy.
- The methods we cover are general enough for both settings.
30
Probabilistic Classification
- In many cases an algorithm will predict a single "best" class.
- Predict a customer will purchase Gucci.
31
Probabilistic Classification
- In many cases an algorithm will predict a single "best" class.
- Predict a customer will purchase Gucci.
- In other instances an algorithm will provide probabilities.
- The customer has a 40% chance of purchasing Gucci, a 35% of chance of purchasing Givenchy and a 25% chance of purchasing YSL.
31
Probabilistic Classification
- A probabilistic prediction can be converted to a point prediction.
32
Probabilistic Classification
- A probabilistic prediction can be converted to a point prediction.
- Simply choose the class with the highest probability.
32
Probabilistic Classification
- A probabilistic prediction can be converted to a point prediction.
- Simply choose the class with the highest probability.
- In the example on the previous slide the choice would be Gucci.
32
Two class case
- In the two class case, choosing the class with highest probability is simple.
33
Two class case
- In the two class case, choosing the class with highest probability is simple.
- Assign to a class if the probability is greater than 0.5
33
Two class case
- In the two class case, choosing the class with highest probability is simple.
- Assign to a class if the probability is greater than 0.5
- In some applications a different threshold may be used.
33
Two class case
- In the two class case, choosing the class with highest probability is simple.
- Assign to a class if the probability is greater than 0.5
- In some applications a different threshold may be used.
- This is particularly the case if there are asymmetric costs involved with different types of misclassification.
33
An example
- Suppose you work for the tax office.
34
An example
- Suppose you work for the tax office.
- You need to decide who should be audited and who should not be audited.
34
An example
- Suppose you work for the tax office.
- You need to decide who should be audited and who should not be audited.
- When doing classification you can make two mistakes
- Audit an innocent person
- Fail to audit a guilty person
- Are these mistakes equally costly?
34
Tax example
- Auditing an innocent person is costly since resources are used for no gain.
- Suppose it costs $100 to audit a person.
- Failing to audit a guilty person is costly since there is a failure to recover tax revenue.
- Let $500 be recovered from the guilty.
- In this example, it is more costly to fail to audit the guilty.
- However, misclassification rate treats both errors the same.
35
Sensitivity v Specificity
- In a 2-class problem think of one class as the presence of a condition and the other class as the absence of a condition.
36
Sensitivity v Specificity
- In a 2-class problem think of one class as the presence of a condition and the other class as the absence of a condition.
- In the auditing example the condition can be that the person is guilty.
36
Sensitivity v Specificity
- In a 2-class problem think of one class as the presence of a condition and the other class as the absence of a condition.
- In the auditing example the condition can be that the person is guilty.
- Sensitivity refers to the true positive rate. The proportion of guilty classified as guilty.
36
Sensitivity v Specificity
- In a 2-class problem think of one class as the presence of a condition and the other class as the absence of a condition.
- In the auditing example the condition can be that the person is guilty.
- Sensitivity refers to the true positive rate. The proportion of guilty classified as guilty.
- Specificity refers to the true negative rate. The proportion of innocent classified as innocent.
36
Sensitivity v Specificity
- Consider that we audit when the probability of being guilty is greater than 50%.
37
Sensitivity v Specificity
- Consider that we audit when the probability of being guilty is greater than 50%.
- Changing this threshold can change the sensitivity and specificity.
37
Sensitivity v Specificity
- Consider that we audit when the probability of being guilty is greater than 50%.
- Changing this threshold can change the sensitivity and specificity.
- Reducing the threshold to 0 means everyone is audited. The sensitivity will be perfect but specificity will be zero.
37
Sensitivity v Specificity
- Consider that we audit when the probability of being guilty is greater than 50%.
- Changing this threshold can change the sensitivity and specificity.
- Reducing the threshold to 0 means everyone is audited. The sensitivity will be perfect but specificity will be zero.
- Raising the threshold to 1 means no one is audited. The specificity will be perfect but sensitivity will be zero.
37
Example
| Person | Pred. Pr. Guilty | Truth |
|---|---|---|
| A | 0.3 | Not Guilty |
| B | 0.4 | Guilty |
| C | 0.6 | Guilty |
| D | 0.7 | Guilty |
38
Questions
- For a threshold of 0.5
- What is your prediction for each individual?
- What is the misclassification error?
- What is the sensitivity?
- What is the specificity?
- What is the cost?
39
Answer
| Person | Pred. Pr. Guilty | Prediction | Truth |
|---|---|---|---|
| A | 0.3 | Not Guilty | Not Guilty |
| B | 0.4 | Not Guilty | Guilty |
| C | 0.6 | Guilty | Guilty |
| D | 0.7 | Guilty | Guilty |
40
Answers
- Misclassification error is 0.25.
- Sensitivity is 0.6667
- Specificity is 1
- Cost is $500
41
Your turn
- How do the answers change when the threshold is 0.2?
- How do the answers change when the threshold is 0.65?
42
Answer (Threshold 0.2)
| Person | Pred. Pr. Guilty | Prediction | Truth |
|---|---|---|---|
| A | 0.3 | Guilty | Not Guilty |
| B | 0.4 | Guilty | Guilty |
| C | 0.6 | Guilty | Guilty |
| D | 0.7 | Guilty | Guilty |
43
Answers
- Misclassification error is 0.25.
- Sensitivity is 1
- Specificity is 0
- Cost is $100
44
Answer (Threshold 0.65)
| Person | Pred. Pr. Guilty | Prediction | Truth |
|---|---|---|---|
| A | 0.3 | Not Guilty | Not Guilty |
| B | 0.4 | Not Guilty | Guilty |
| C | 0.6 | Not Guilty | Guilty |
| D | 0.7 | Guilty | Guilty |
45
Answers
- Misclassification error is 0.5.
- Sensitivity is 0.333
- Specificity is 1
- Cost is $1000
46
Conclusion
- For the remainder of the unit the focus is on different ways to do classification.
47
Conclusion
- For the remainder of the unit the focus is on different ways to do classification.
- In a business (and any other setting) be aware that
- Correlation does not imply causation
- Prediction should be thought about probabilistically.
- Cost should be taken into account when classification is used in decision making.
47