Nearest Neighbour Classification
Data Visualisation and Analytics
Anastasios Panagiotelis and Lauren Kennedy
Lecture 9
1
Love Thy Neighbour
2
Nearest Neighbours
- Recall that we discussed nearest neigbours during the topic on LOESS.
3
Nearest Neighbours
- Recall that we discussed nearest neigbours during the topic on LOESS.
- Now we will use nearest neighbours in the context of classification.
3
Nearest Neighbours
- Recall that we discussed nearest neigbours during the topic on LOESS.
- Now we will use nearest neighbours in the context of classification.
- Illustration with 2 predictors since these are easy to understand.
3
Nearest Neighbours
- Recall that we discussed nearest neigbours during the topic on LOESS.
- Now we will use nearest neighbours in the context of classification.
- Illustration with 2 predictors since these are easy to understand.
- Data is a subsample of 100 observations from the Credit default data.
3
Credit Data
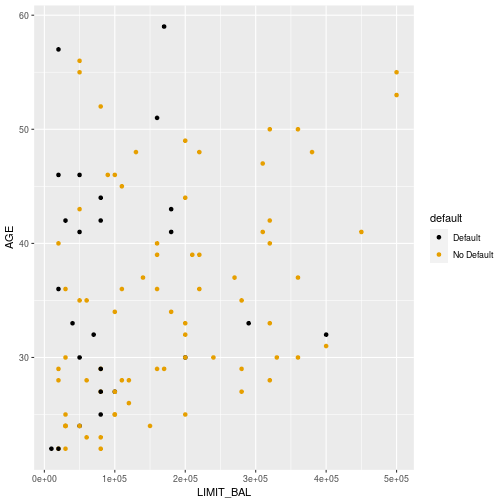
4
Default or not?
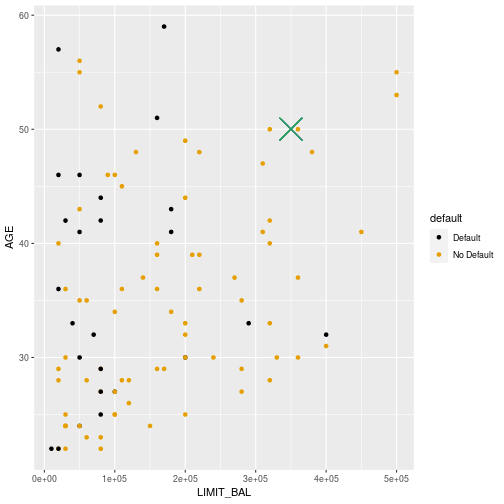
5
Default or not?
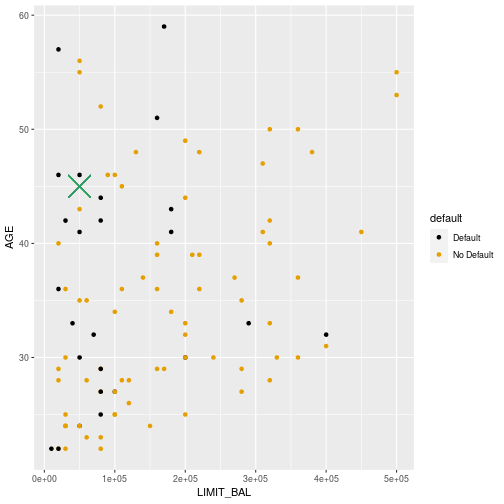
6
Basic Idea
- For the first point (limit 350000, age 50) most nearby points in the training data are not defaults (orange).
- Predict no default
- For the second point (limit 50000, age 45) most nearby points in the training data are defaults (black).
- Predict default
7
More formally
- Concentrate on the k nearest points, also known as the k Nearest Neighbours or k-NN.
- Let Nx,k be the set of k training points closest to x.
- The predicted probability of Default is
1k∑i∈Nx,kI(yi=Default)
8
First example (k=4)
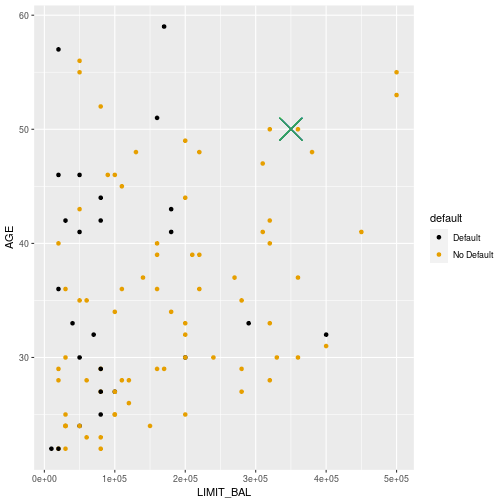
9
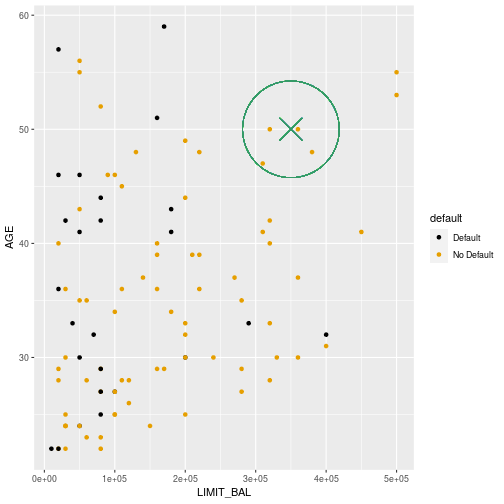
First example (k=4)
10
Prediction
- The four nearest neighbours are all Non-defaults
11
Prediction
- The four nearest neighbours are all Non-defaults
- Therefore the predicted default probability for an individual with limit of 350000 and age 50 is zero.
11
Prediction
- The four nearest neighbours are all Non-defaults
- Therefore the predicted default probability for an individual with limit of 350000 and age 50 is zero.
- We predict this individual does not default.
11
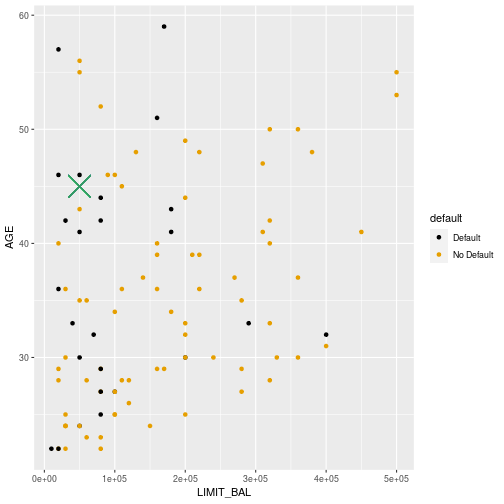
Second example (k=4)
12
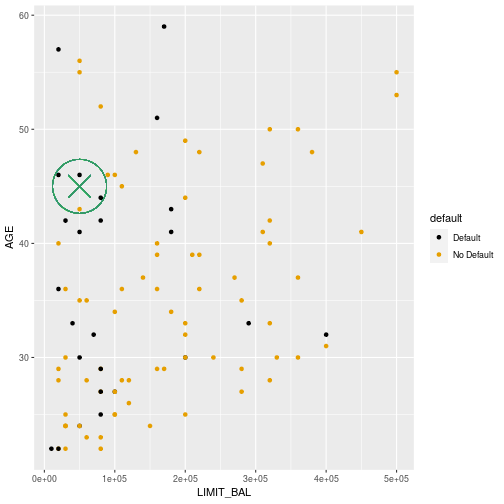
Second example (k=4)
13
Prediction
- The four nearest neighbours include three Defaults and one Non-default
14
Prediction
- The four nearest neighbours include three Defaults and one Non-default
- Therefore the predicted default probability for an individual with limit of 50000 and age 45 is 0.75.
14
Prediction
- The four nearest neighbours include three Defaults and one Non-default
- Therefore the predicted default probability for an individual with limit of 50000 and age 45 is 0.75.
- Using a threshold of 0.5, we predict this individual does default.
14
Prediction
- The four nearest neighbours include three Defaults and one Non-default
- Therefore the predicted default probability for an individual with limit of 50000 and age 45 is 0.75.
- Using a threshold of 0.5, we predict this individual does default.
- In practice a different threshold can be used.
14
Your Turn
- Consider the case where k=10
- What is the predicted probability of default for the first example (350000 limit 50 years age)?
- What is the predicted probability of default for the second example (50000 limit 45 years age)?
15
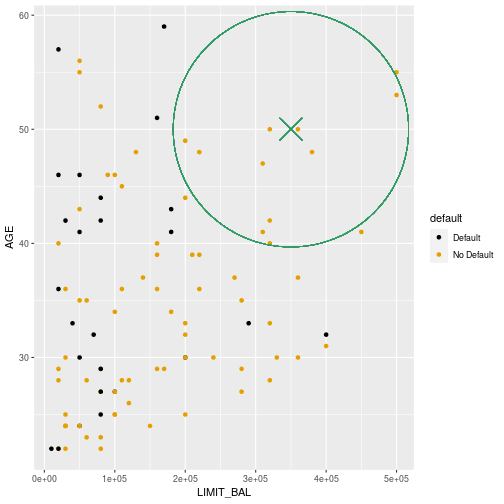
First example (k=10)
16
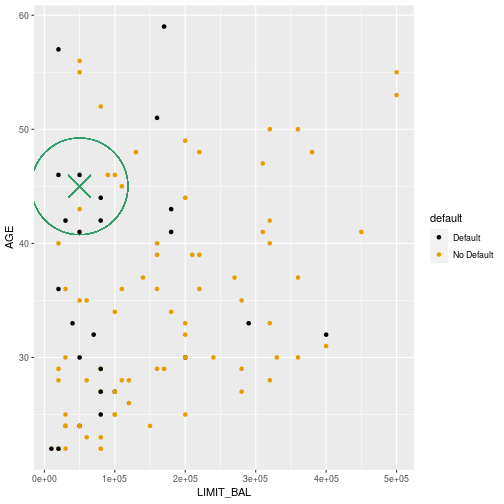
Second example (k=10)
17
Answers
- What is the predicted probability of default for the first example (350000 limit 50 years age)?
- The predicted probability of default is 0.
- What is the predicted probability of default for the second example (50000 limit 45 years age)?
- The predicted probability of default is 0.6.
18
Decision Boundary
19
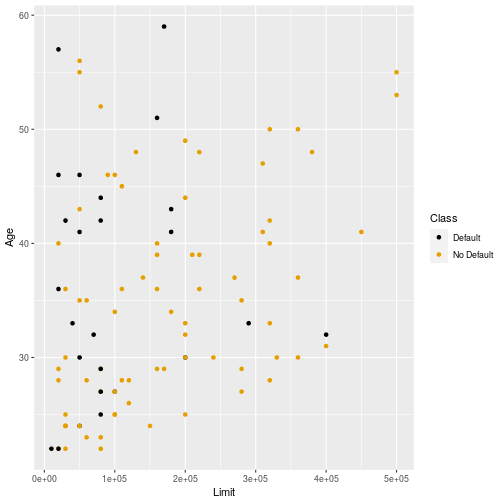
Data again
20
Decision Boundaries
- For the next few slides a grid of evaluation points has been created.
- If k-NN predicts "Default" the grid point is colored black.
- If k-NN predicts "No default" the grid point is colored yellow.
- Plotting these gives an idea of the decision boundaries.
21
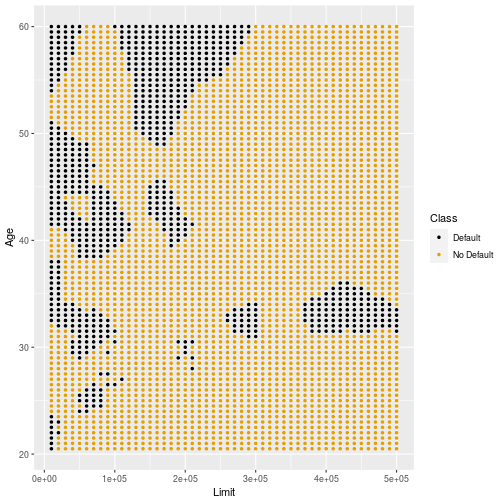
Decision boundary (k=1)
22
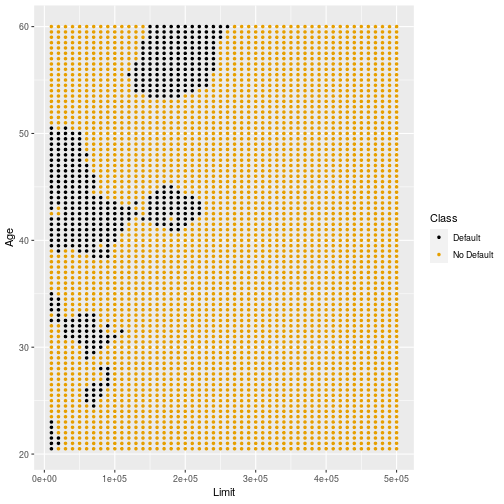
Decision boundary (k=3)
23
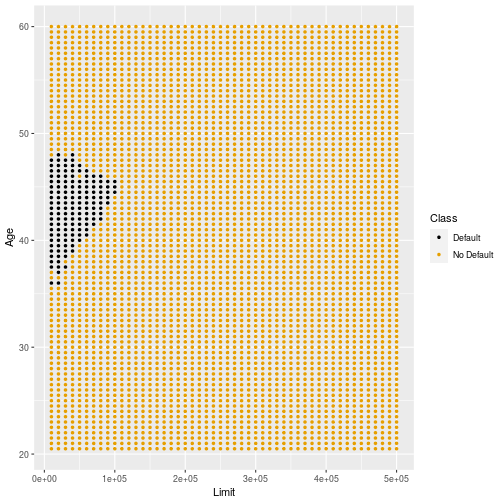
Decision boundary (k=11)
24
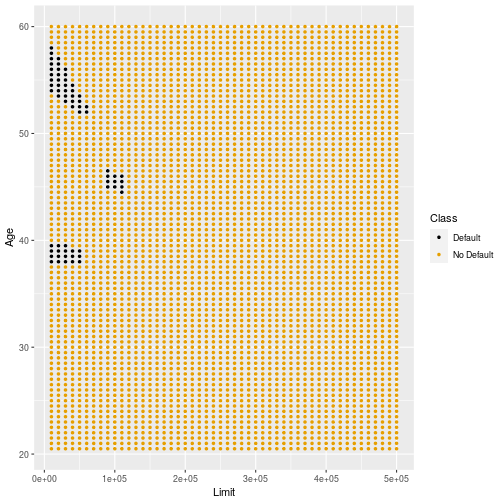
Decision boundary (k=17)
25
Choosing k
- Smaller values of k lead to very complicated decision boundaries.
- Larger values of k provide smoother boundaries although there are still some unstable regions.
- Larger values of k also slow down computation for big datasets.
26
Choosing k
- A general rule of thumb is to choose k≈√n
27
Choosing k
- A general rule of thumb is to choose k≈√n
- Also it is advised to choose a value of k that is NOT a multiple of the number of classes.
27
Choosing k
- A general rule of thumb is to choose k≈√n
- Also it is advised to choose a value of k that is NOT a multiple of the number of classes.
- This avoids ties.
27
Choosing k
- A general rule of thumb is to choose k≈√n
- Also it is advised to choose a value of k that is NOT a multiple of the number of classes.
- This avoids ties.
- When ties are present, a class is chosen randomly.
27
Choosing k
- A general rule of thumb is to choose k≈√n
- Also it is advised to choose a value of k that is NOT a multiple of the number of classes.
- This avoids ties.
- When ties are present, a class is chosen randomly.
- For the two class problem, choose odd k.
27
Choosing k
- Finally, data can be split into a training sample and test sample.
28
Choosing k
- Finally, data can be split into a training sample and test sample.
- We can then try many possible values of k.
28
Choosing k
- Finally, data can be split into a training sample and test sample.
- We can then try many possible values of k.
- The optimal value can be selected so that the test misclassification error rate is minimised.
28
Choosing k
- Finally, data can be split into a training sample and test sample.
- We can then try many possible values of k.
- The optimal value can be selected so that the test misclassification error rate is minimised.
- Another alternative is to use cross validation.
28
Instability of kNN
29
High variability
- A problem of k-NN classification is that it is highly variable.
30
High variability
- A problem of k-NN classification is that it is highly variable.
- Now assume we use a fixed value of k but make small changes in the training data
30
High variability
- A problem of k-NN classification is that it is highly variable.
- Now assume we use a fixed value of k but make small changes in the training data
- This change the decision boundaries dramatically.
30
High variability
- A problem of k-NN classification is that it is highly variable.
- Now assume we use a fixed value of k but make small changes in the training data
- This change the decision boundaries dramatically.
- This is much more pronounced for smaller values of k.
30
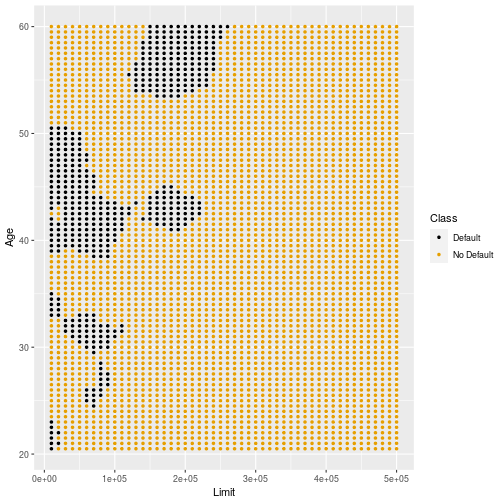
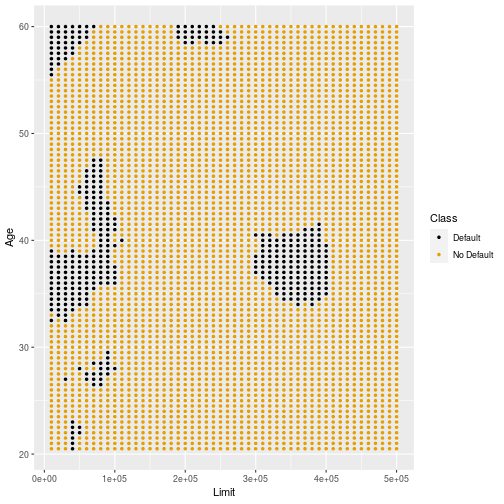
High variability
- A problem of k-NN classification is that it is highly variable.
- Now assume we use a fixed value of k but make small changes in the training data
- This change the decision boundaries dramatically.
- This is much more pronounced for smaller values of k.
- The next few slides show different subsamples of training data.
30
Original Training Sample (k=3)
31
Different Training Sample (k=3)
32
Original Training Sample (k=11)
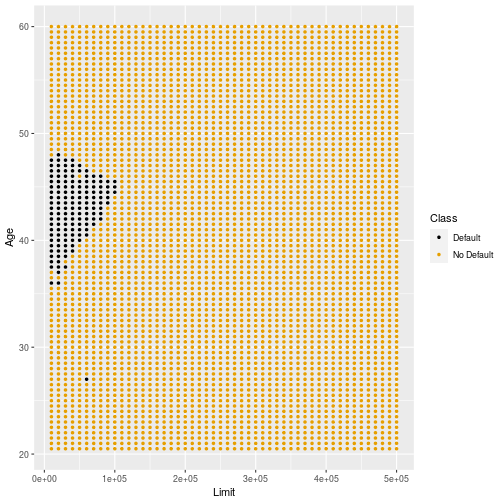
33
Different Training Sample (k=11)
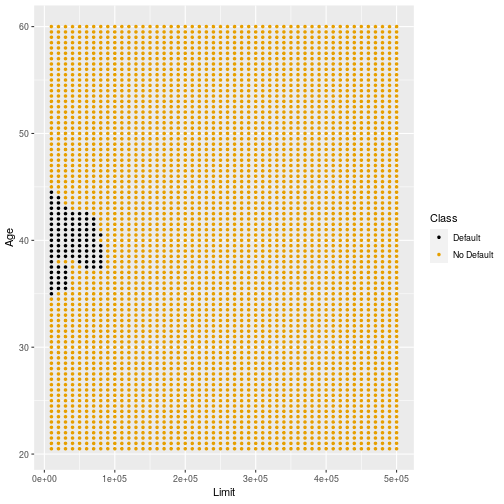
34
An ethical problem
- A classifier with such high variability obviously poses statistical problems.
35
An ethical problem
- A classifier with such high variability obviously poses statistical problems.
- It also poses ethical issues.
35
An ethical problem
- A classifier with such high variability obviously poses statistical problems.
- It also poses ethical issues.
- Suppose the algorithm is used to decide who recieves a loan or who is audited by the tax office.
35
An ethical problem
- A classifier with such high variability obviously poses statistical problems.
- It also poses ethical issues.
- Suppose the algorithm is used to decide who recieves a loan or who is audited by the tax office.
- It should be possible to clearly explain to this person why their loan application was rejected or why they were chosen for audit.
35
An ethical problem
- A classifier with such high variability obviously poses statistical problems.
- It also poses ethical issues.
- Suppose the algorithm is used to decide who recieves a loan or who is audited by the tax office.
- It should be possible to clearly explain to this person why their loan application was rejected or why they were chosen for audit.
- Having such a sensitive algorithm makes this difficult.
35
k-NN Classification in R
36
Package
- The k-NN algorithm can be implemented using the
classpackage.
37
Package
- The k-NN algorithm can be implemented using the
classpackage. - We will go through an example using the data that has already been cleaned and is in the file knnexample.RData
37
Package
- The k-NN algorithm can be implemented using the
classpackage. - We will go through an example using the data that has already been cleaned and is in the file knnexample.RData
- Load this file using
load('knnexample.RData')37
Data
- A data frame of 250 randomly selected training observations for the predictors LIMIT_BAL and AGE (
train_x)
38
Data
- A data frame of 250 randomly selected training observations for the predictors LIMIT_BAL and AGE (
train_x) - The values of the target variable for the training data stored as a factor (
train_y)
38
Data
- A data frame of 250 randomly selected training observations for the predictors LIMIT_BAL and AGE (
train_x) - The values of the target variable for the training data stored as a factor (
train_y) - A data frame of 250 randomly selected test observations for the predictors LIMIT_BAL and AGE (
test_x)
38
Data
- A data frame of 250 randomly selected training observations for the predictors LIMIT_BAL and AGE (
train_x) - The values of the target variable for the training data stored as a factor (
train_y) - A data frame of 250 randomly selected test observations for the predictors LIMIT_BAL and AGE (
test_x) - The values of the target variable for the test data stored as a factor (
test_y)
38
Standardisation
- An important issue with k-NN is that distances can be sensitive to units of measurement.
39
Standardisation
- An important issue with k-NN is that distances can be sensitive to units of measurement.
- For this reason we should standardise so that all predictors have a standard deviation of 1.
train_x_std<-scale(train_x)mean_train_x<-attr(train_x_std,"scaled:center")std_train_x<-attr(train_x_std,"scaled:scale")39
Standardise training data
- The test data should also be standardised
- This tranformation should be identical for training and test data so using the mean and standard deviation of the training data.
test_x_std<-scale(test_x, center = mean_train_x, scale = std_train_x)- Now the data are ready to be used in the
knnfunction
40
Using knn
With k=1
knn(train_x_std,test_x_std, train_y,k=1)->yhat_k1print(yhat_k1)## [1] No Default Default Default Default No Default No Default## [7] No Default No Default No Default Default No Default No Default## [13] No Default No Default No Default Default No Default No Default## [19] No Default No Default Default No Default Default Default ## [25] No Default No Default Default No Default Default No Default## [31] Default No Default No Default No Default No Default No Default## [37] Default No Default No Default Default Default No Default## [43] No Default No Default No Default No Default Default No Default## [49] No Default No Default Default No Default No Default No Default## [55] No Default No Default No Default Default No Default No Default## [61] Default No Default No Default Default No Default No Default## [67] Default Default No Default No Default No Default No Default## [73] No Default No Default No Default Default No Default No Default## [79] No Default No Default No Default No Default No Default No Default## [85] Default No Default No Default No Default No Default No Default## [91] No Default No Default No Default No Default Default No Default## [97] No Default No Default No Default No Default No Default No Default## [103] No Default No Default No Default No Default Default No Default## [109] No Default Default No Default No Default No Default Default ## [115] No Default No Default No Default No Default No Default No Default## [121] No Default No Default Default No Default Default No Default## [127] No Default Default No Default No Default No Default No Default## [133] No Default No Default No Default No Default No Default No Default## [139] No Default No Default Default No Default Default No Default## [145] Default No Default No Default No Default No Default No Default## [151] No Default No Default No Default Default No Default Default ## [157] No Default No Default No Default No Default No Default Default ## [163] No Default No Default No Default No Default No Default No Default## [169] No Default No Default No Default No Default No Default No Default## [175] No Default No Default No Default Default Default No Default## [181] No Default No Default No Default Default No Default No Default## [187] No Default No Default Default No Default Default No Default## [193] Default No Default No Default No Default No Default No Default## [199] Default No Default No Default Default Default No Default## [205] No Default No Default No Default No Default Default No Default## [211] No Default No Default No Default No Default Default No Default## [217] No Default No Default No Default Default No Default No Default## [223] No Default Default No Default No Default No Default No Default## [229] No Default No Default No Default No Default No Default No Default## [235] No Default No Default No Default No Default No Default No Default## [241] Default No Default No Default Default No Default Default ## [247] No Default No Default No Default No Default## Levels: Default No Default41
Test misclassification rate
To compute test misclassification
miscl_k1<-mean(test_y!=yhat_k1)print(miscl_k1)## [1] 0.32Overall, 32% of the test sample is incorrectly predicted
42
Test misclassification rate
To compute test misclassification
miscl_k1<-mean(test_y!=yhat_k1)print(miscl_k1)## [1] 0.32Overall, 32% of the test sample is incorrectly predicted
- As an exercise, you can now try to obtain the misclassification rate with k=5
42
Answer
knn(train_x_std, test_x_std, train_y,k=5)->yhat_k5miscl_k5<-mean(test_y!=yhat_k5)print(miscl_k5)## [1] 0.292The misclassification rate when k=5 is 0.292.
43
Sensitivity and specificity
- It is also worth reporting results in a cross tabulation
table(test_y,yhat_k5)## yhat_k5## test_y Default No Default## Default 8 52## No Default 21 169Letting "default" be the "positive" class, sensitivity is 8/(8+52) or 0.133, and specificity is 169/(21+169) or 0.889
44
Additional features
- If the argument
prob=TRUEis included then the function returns probabilities.
knn(train_x_std, test_x_std, train_y,k=5,prob = TRUE)->prob_k545
Predictions
- The output still contains predictions
print(prob_k5)## [1] No Default Default No Default No Default Default No Default## [7] No Default No Default No Default Default No Default No Default## [13] No Default No Default No Default No Default No Default No Default## [19] No Default No Default Default No Default No Default No Default## [25] No Default No Default No Default No Default Default No Default## [31] No Default No Default No Default Default Default No Default## [37] No Default No Default No Default No Default No Default No Default## [43] No Default No Default No Default No Default No Default No Default## [49] No Default No Default No Default Default Default No Default## [55] No Default Default Default Default No Default Default ## [61] Default No Default Default Default No Default No Default## [67] No Default No Default No Default No Default No Default No Default## [73] No Default No Default No Default No Default No Default No Default## [79] No Default No Default No Default No Default No Default No Default## [85] No Default No Default No Default No Default No Default No Default## [91] No Default No Default No Default No Default Default No Default## [97] No Default No Default No Default No Default No Default No Default## [103] No Default Default No Default Default No Default No Default## [109] No Default No Default No Default No Default No Default No Default## [115] No Default No Default No Default Default No Default No Default## [121] No Default No Default No Default No Default No Default No Default## [127] No Default Default No Default No Default No Default No Default## [133] No Default No Default No Default No Default No Default No Default## [139] No Default No Default No Default Default No Default No Default## [145] No Default No Default No Default No Default No Default No Default## [151] No Default No Default No Default No Default No Default No Default## [157] No Default No Default No Default No Default No Default No Default## [163] No Default No Default Default No Default No Default No Default## [169] No Default No Default No Default No Default No Default No Default## [175] Default No Default No Default No Default Default No Default## [181] No Default No Default No Default No Default No Default No Default## [187] No Default No Default No Default No Default No Default No Default## [193] No Default No Default No Default No Default No Default No Default## [199] No Default No Default No Default No Default Default No Default## [205] No Default No Default No Default No Default No Default No Default## [211] No Default No Default No Default No Default No Default No Default## [217] No Default No Default No Default No Default No Default No Default## [223] No Default No Default No Default No Default No Default No Default## [229] No Default No Default No Default No Default No Default No Default## [235] No Default No Default Default No Default No Default No Default## [241] No Default No Default No Default Default No Default No Default## [247] No Default No Default No Default No Default## attr(,"prob")## [1] 1.0000000 0.5714286 0.6666667 0.6000000 0.6000000 0.8000000 1.0000000## [8] 1.0000000 0.6666667 0.6000000 0.8333333 0.8000000 1.0000000 0.5714286## [15] 1.0000000 0.6666667 1.0000000 1.0000000 0.6000000 1.0000000 0.6000000## [22] 0.8333333 0.6666667 0.6000000 1.0000000 1.0000000 0.5714286 1.0000000## [29] 0.6000000 0.5000000 0.6666667 0.8571429 1.0000000 0.6000000 0.6000000## [36] 0.8000000 0.6666667 0.6000000 0.6000000 0.5000000 0.6000000 0.6666667## [43] 0.6000000 0.6000000 0.8333333 1.0000000 0.6666667 0.8000000 1.0000000## [50] 1.0000000 0.8000000 0.6000000 0.6000000 1.0000000 1.0000000 0.6000000## [57] 0.6666667 0.8000000 1.0000000 0.6000000 0.8000000 1.0000000 0.6000000## [64] 0.6000000 0.6666667 0.8000000 0.5714286 0.5714286 1.0000000 1.0000000## [71] 0.6666667 0.6000000 1.0000000 0.6666667 0.8000000 0.8000000 1.0000000## [78] 0.8000000 0.8000000 1.0000000 0.6666667 0.6000000 1.0000000 0.8000000## [85] 0.5714286 1.0000000 0.8000000 0.6666667 1.0000000 0.8750000 1.0000000## [92] 1.0000000 0.8000000 0.7142857 0.6000000 0.7142857 1.0000000 0.8571429## [99] 0.8000000 0.8000000 0.8333333 0.8000000 0.5714286 0.6000000 0.8333333## [106] 0.6000000 0.8000000 1.0000000 1.0000000 0.6666667 1.0000000 1.0000000## [113] 1.0000000 0.6000000 0.8750000 0.6000000 1.0000000 0.6666667 1.0000000## [120] 1.0000000 0.6000000 0.8333333 0.5000000 0.6000000 0.6000000 0.6666667## [127] 1.0000000 0.6000000 0.7142857 1.0000000 0.8000000 0.8333333 1.0000000## [134] 0.6000000 0.7142857 1.0000000 0.6000000 0.8000000 0.6666667 0.7142857## [141] 0.6000000 0.6666667 0.8000000 0.8000000 0.8000000 1.0000000 1.0000000## [148] 1.0000000 0.8000000 1.0000000 0.8750000 1.0000000 1.0000000 0.6000000## [155] 1.0000000 0.8000000 0.6666667 1.0000000 0.5714286 0.8000000 0.6000000## [162] 0.6000000 1.0000000 0.6000000 0.6000000 0.8000000 1.0000000 1.0000000## [169] 1.0000000 0.5714286 1.0000000 0.5000000 0.8000000 0.7142857 0.6000000## [176] 0.6666667 1.0000000 0.8750000 0.6666667 1.0000000 1.0000000 0.8000000## [183] 0.8000000 0.6666667 0.6000000 0.8000000 0.8000000 0.8000000 0.6000000## [190] 0.8000000 0.8000000 0.8333333 0.8000000 0.6000000 1.0000000 0.6666667## [197] 0.8000000 0.8000000 0.8750000 0.8333333 0.7142857 0.7500000 0.6000000## [204] 1.0000000 1.0000000 1.0000000 0.8000000 1.0000000 0.8000000 1.0000000## [211] 0.7142857 1.0000000 1.0000000 0.6666667 0.6000000 1.0000000 1.0000000## [218] 0.8000000 0.8333333 0.6666667 1.0000000 0.7500000 0.8000000 0.5714286## [225] 0.8000000 1.0000000 0.8000000 1.0000000 0.8000000 1.0000000 1.0000000## [232] 1.0000000 1.0000000 0.8333333 0.6000000 1.0000000 0.6000000 0.8000000## [239] 1.0000000 0.6000000 0.8000000 1.0000000 1.0000000 0.6000000 0.8333333## [246] 0.6666667 1.0000000 0.8000000 0.8000000 1.0000000## Levels: Default No Default46
Probabilities
- Probabilities can be stripped out using the
attrfunction
print(attr(prob_k5,"prob"))## [1] 1.0000000 0.5714286 0.6666667 0.6000000 0.6000000 0.8000000 1.0000000## [8] 1.0000000 0.6666667 0.6000000 0.8333333 0.8000000 1.0000000 0.5714286## [15] 1.0000000 0.6666667 1.0000000 1.0000000 0.6000000 1.0000000 0.6000000## [22] 0.8333333 0.6666667 0.6000000 1.0000000 1.0000000 0.5714286 1.0000000## [29] 0.6000000 0.5000000 0.6666667 0.8571429 1.0000000 0.6000000 0.6000000## [36] 0.8000000 0.6666667 0.6000000 0.6000000 0.5000000 0.6000000 0.6666667## [43] 0.6000000 0.6000000 0.8333333 1.0000000 0.6666667 0.8000000 1.0000000## [50] 1.0000000 0.8000000 0.6000000 0.6000000 1.0000000 1.0000000 0.6000000## [57] 0.6666667 0.8000000 1.0000000 0.6000000 0.8000000 1.0000000 0.6000000## [64] 0.6000000 0.6666667 0.8000000 0.5714286 0.5714286 1.0000000 1.0000000## [71] 0.6666667 0.6000000 1.0000000 0.6666667 0.8000000 0.8000000 1.0000000## [78] 0.8000000 0.8000000 1.0000000 0.6666667 0.6000000 1.0000000 0.8000000## [85] 0.5714286 1.0000000 0.8000000 0.6666667 1.0000000 0.8750000 1.0000000## [92] 1.0000000 0.8000000 0.7142857 0.6000000 0.7142857 1.0000000 0.8571429## [99] 0.8000000 0.8000000 0.8333333 0.8000000 0.5714286 0.6000000 0.8333333## [106] 0.6000000 0.8000000 1.0000000 1.0000000 0.6666667 1.0000000 1.0000000## [113] 1.0000000 0.6000000 0.8750000 0.6000000 1.0000000 0.6666667 1.0000000## [120] 1.0000000 0.6000000 0.8333333 0.5000000 0.6000000 0.6000000 0.6666667## [127] 1.0000000 0.6000000 0.7142857 1.0000000 0.8000000 0.8333333 1.0000000## [134] 0.6000000 0.7142857 1.0000000 0.6000000 0.8000000 0.6666667 0.7142857## [141] 0.6000000 0.6666667 0.8000000 0.8000000 0.8000000 1.0000000 1.0000000## [148] 1.0000000 0.8000000 1.0000000 0.8750000 1.0000000 1.0000000 0.6000000## [155] 1.0000000 0.8000000 0.6666667 1.0000000 0.5714286 0.8000000 0.6000000## [162] 0.6000000 1.0000000 0.6000000 0.6000000 0.8000000 1.0000000 1.0000000## [169] 1.0000000 0.5714286 1.0000000 0.5000000 0.8000000 0.7142857 0.6000000## [176] 0.6666667 1.0000000 0.8750000 0.6666667 1.0000000 1.0000000 0.8000000## [183] 0.8000000 0.6666667 0.6000000 0.8000000 0.8000000 0.8000000 0.6000000## [190] 0.8000000 0.8000000 0.8333333 0.8000000 0.6000000 1.0000000 0.6666667## [197] 0.8000000 0.8000000 0.8750000 0.8333333 0.7142857 0.7500000 0.6000000## [204] 1.0000000 1.0000000 1.0000000 0.8000000 1.0000000 0.8000000 1.0000000## [211] 0.7142857 1.0000000 1.0000000 0.6666667 0.6000000 1.0000000 1.0000000## [218] 0.8000000 0.8333333 0.6666667 1.0000000 0.7500000 0.8000000 0.5714286## [225] 0.8000000 1.0000000 0.8000000 1.0000000 0.8000000 1.0000000 1.0000000## [232] 1.0000000 1.0000000 0.8333333 0.6000000 1.0000000 0.6000000 0.8000000## [239] 1.0000000 0.6000000 0.8000000 1.0000000 1.0000000 0.6000000 0.8333333## [246] 0.6666667 1.0000000 0.8000000 0.8000000 1.000000047
Prediction and Probabilities
| Prediction | Probability |
|---|---|
| No Default | 1.0000000 |
| Default | 0.5714286 |
| No Default | 0.6666667 |
| No Default | 0.6000000 |
- For the first observation the probability of No Default is 1, but for the second observation the probablity of Default is 0.5714.
48
Prediction and Probabilities
| Prediction | Probability |
|---|---|
| No Default | 1.0000000 |
| Default | 0.5714286 |
| No Default | 0.6666667 |
| No Default | 0.6000000 |
- For the first observation the probability of No Default is 1, but for the second observation the probablity of Default is 0.5714.
- The probability is relative to the prediction.
48
Ties in neighbours
- If there are only 5 neighbours all probabilities should be either 0.6, 0.8 or 1.
49
Ties in neighbours
- If there are only 5 neighbours all probabilities should be either 0.6, 0.8 or 1.
- This is not true. Why?
49
Ties in neighbours
- If there are only 5 neighbours all probabilities should be either 0.6, 0.8 or 1.
- This is not true. Why?
- There can be ties in finding the nearest neighbours.
49
Ties in neighbours
- If there are only 5 neighbours all probabilities should be either 0.6, 0.8 or 1.
- This is not true. Why?
- There can be ties in finding the nearest neighbours.
- Two (or more) observations may tied as equally fifth closest.
49
Ties in neighbours
- If there are only 5 neighbours all probabilities should be either 0.6, 0.8 or 1.
- This is not true. Why?
- There can be ties in finding the nearest neighbours.
- Two (or more) observations may tied as equally fifth closest.
- In this case both are used.
49
Regression
- The same principle can be used for regression.
50
Regression
- The same principle can be used for regression.
- The predicted value is simply the average value of y for the k-nearest neighbours.
50
Regression
- The same principle can be used for regression.
- The predicted value is simply the average value of y for the k-nearest neighbours.
- This leads to a highly non-linear regression function.
50
Conclusion
- Using k-NN is a simple but often effective method for classification.
51
Conclusion
- Using k-NN is a simple but often effective method for classification.
- There are limitations
51
Conclusion
- Using k-NN is a simple but often effective method for classification.
- There are limitations
- Complicated decision boundaries.
- High variance.
- Also it works poorly when there is a large number of predictors.
51