Discriminant Analysis
Data Visualisation and Analytics
Anastasios Panagiotelis and Lauren Kennedy
Lecture 10
1
The power of Bayes
2
Credit Data
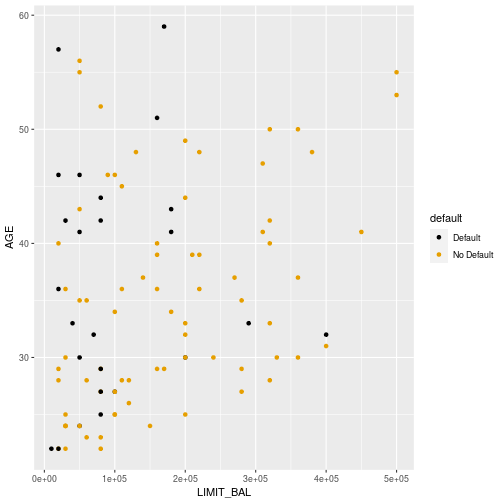
3
Default or not?
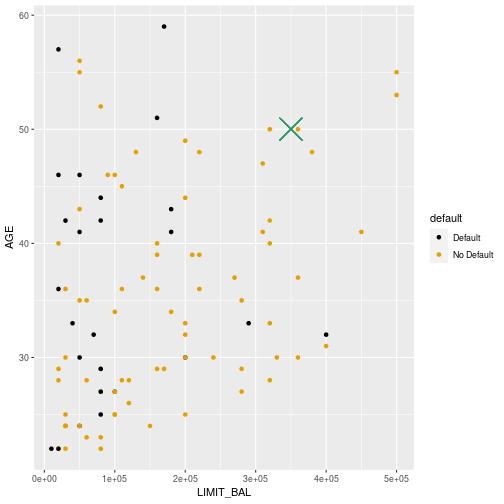
4
Default or not?
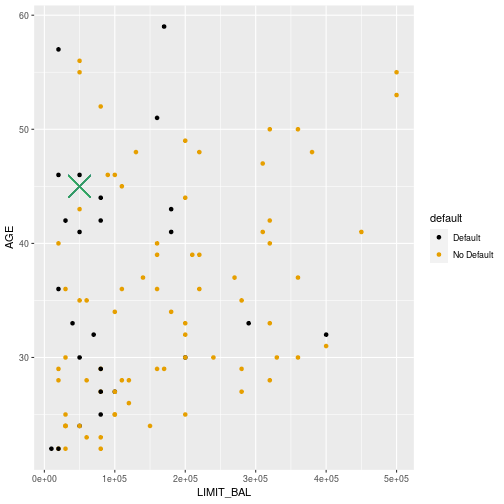
5
Notation
- In general y is the target. In this example it can take two values, let y=1 in case of default and y=0 in case of non-default.
6
Notation
- In general y is the target. In this example it can take two values, let y=1 in case of default and y=0 in case of non-default.
- In general x are the predictors. In this example they are age and limit balance.
6
Notation
- In general y is the target. In this example it can take two values, let y=1 in case of default and y=0 in case of non-default.
- In general x are the predictors. In this example they are age and limit balance.
- We would like to find
p(y=1|x)andp(y=0|x)
- If p(y=1|x)>p(y=0|x) we predict default otherwise predict no default.
6
A perfect world
- Ideally we would know three distributions.
- p(x|y=1)
- p(x|y=0)
- p(y)
7
A perfect world
- Ideally we would know three distributions.
- p(x|y=1)
- p(x|y=0)
- p(y)
- If we know these three distributions the we can use Bayes Rule to find p(y=1|x)
p(x|y=1)p(y=1)p(x|y=0)p(y=0)+p(x|y=1)p(y=1)
7
The real world
- This classifier theoretically minimises misclassifiation rate. However...
8
The real world
- This classifier theoretically minimises misclassifiation rate. However...
- p(x|y=0) is unknown
8
The real world
- This classifier theoretically minimises misclassifiation rate. However...
- p(x|y=0) is unknown
- Estimate using the y=0 cases in the training data.
8
The real world
- This classifier theoretically minimises misclassifiation rate. However...
- p(x|y=0) is unknown
- Estimate using the y=0 cases in the training data.
- p(x|y=1) is unknown
8
The real world
- This classifier theoretically minimises misclassifiation rate. However...
- p(x|y=0) is unknown
- Estimate using the y=0 cases in the training data.
- p(x|y=1) is unknown
- Estimate using the y=1 cases in the training data.
8
The real world
- This classifier theoretically minimises misclassifiation rate. However...
- p(x|y=0) is unknown
- Estimate using the y=0 cases in the training data.
- p(x|y=1) is unknown
- Estimate using the y=1 cases in the training data.
- p(y=1) and p(y=0) are unknown
8
The real world
- This classifier theoretically minimises misclassifiation rate. However...
- p(x|y=0) is unknown
- Estimate using the y=0 cases in the training data.
- p(x|y=1) is unknown
- Estimate using the y=1 cases in the training data.
- p(y=1) and p(y=0) are unknown
- Estimate using the proportions of y=1 and y=0 cases in the training data.
8
Assumptions
Some commonly made assumptions are:
9
Assumptions
Some commonly made assumptions are:
- Normality: The predictors follow normal distributions for the y=1 group and y=0 group.
9
Assumptions
Some commonly made assumptions are:
- Normality: The predictors follow normal distributions for the y=1 group and y=0 group.
- Homogeneity of Variances and Covariances: The variances and covariances are the same for the y=1 group and y=0 group.
9
Assumptions
Some commonly made assumptions are:
- Normality: The predictors follow normal distributions for the y=1 group and y=0 group.
- Homogeneity of Variances and Covariances: The variances and covariances are the same for the y=1 group and y=0 group.
- Independence: Observations are independent from one another
9
Linear DA
- Under these assumptions, the prediction depends on a linear combination of x.
10
Linear DA
- Under these assumptions, the prediction depends on a linear combination of x.
- This is known as Linear Discriminant Analysis or LDA.
10
Linear DA
- Under these assumptions, the prediction depends on a linear combination of x.
- This is known as Linear Discriminant Analysis or LDA.
- If Homogeneity of Variances and Covariances assumption is dropped then the prediction depends on a quadratic function of x
10
Linear DA
- Under these assumptions, the prediction depends on a linear combination of x.
- This is known as Linear Discriminant Analysis or LDA.
- If Homogeneity of Variances and Covariances assumption is dropped then the prediction depends on a quadratic function of x
- This is known as Quadratic Discriminant Analysis or QDA.
10
Decision Boundary
11
Data again
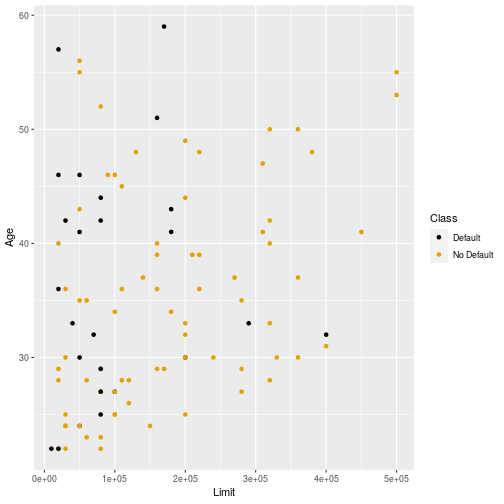
12
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN is presented again.
13
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN is presented again.
- If LDA or QDA predicts "Default" the grid point is colored black.
13
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN is presented again.
- If LDA or QDA predicts "Default" the grid point is colored black.
- If LDA or QDA predicts "No default" the grid point is colored yellow.
13
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN is presented again.
- If LDA or QDA predicts "Default" the grid point is colored black.
- If LDA or QDA predicts "No default" the grid point is colored yellow.
- Think about how these decision boundaries compare to kNN.
13
Decision Boundary: LDA
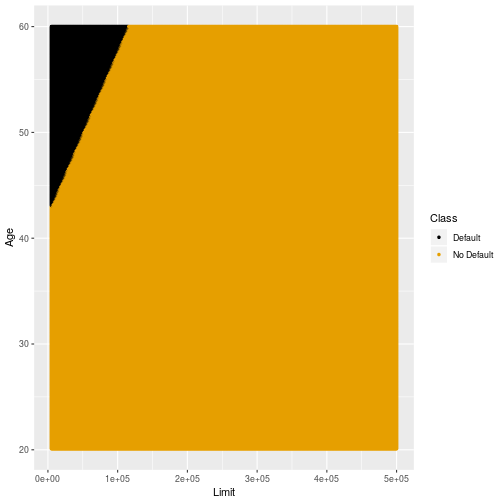
14
Coefficients: LDA
- The coefficient of Limit is 8.6379757×10−6
15
Coefficients: LDA
- The coefficient of Limit is 8.6379757×10−6
- The coefficient of Age is −0.0560362
15
Coefficients: LDA
- The coefficient of Limit is 8.6379757×10−6
- The coefficient of Age is −0.0560362
- It can clearly be explained to a customer that their application was declined since
15
Coefficients: LDA
- The coefficient of Limit is 8.6379757×10−6
- The coefficient of Age is −0.0560362
- It can clearly be explained to a customer that their application was declined since
- Limit that was too low
- Age that was too high.
15
Decision Boundary: QDA
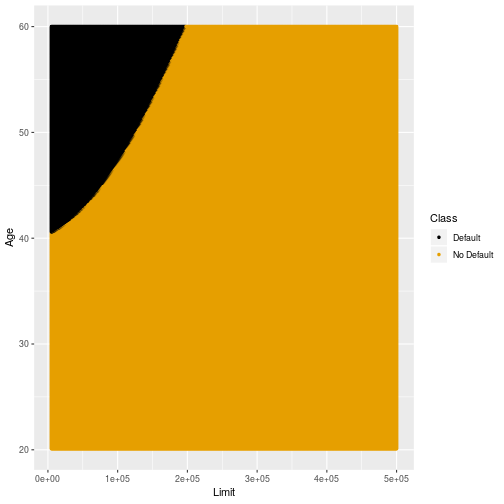
16
Multiclass Example
- On the next few slides we will consider a different dataset where the target variable can take three values.
17
Multiclass Example
- On the next few slides we will consider a different dataset where the target variable can take three values.
- Using the
mpgdataset we will predict whether a car is a 4wd, a rear wheel drive or a front wheel drive.
17
Multiclass Example
- On the next few slides we will consider a different dataset where the target variable can take three values.
- Using the
mpgdataset we will predict whether a car is a 4wd, a rear wheel drive or a front wheel drive. - The predictors will be fuel efficiency on the highway (
hwy) and engine size (displ)
17
Multiclass Example: Data
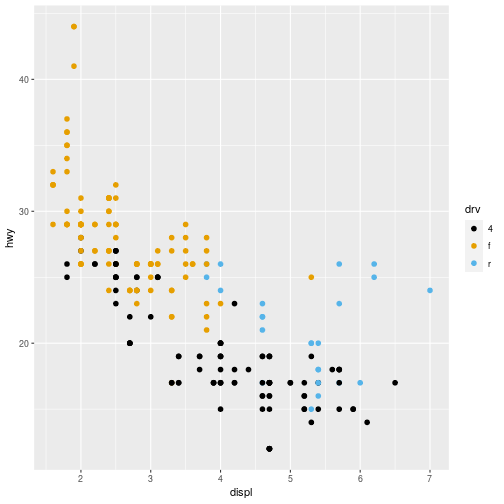
18
Multiclass Example: LDA
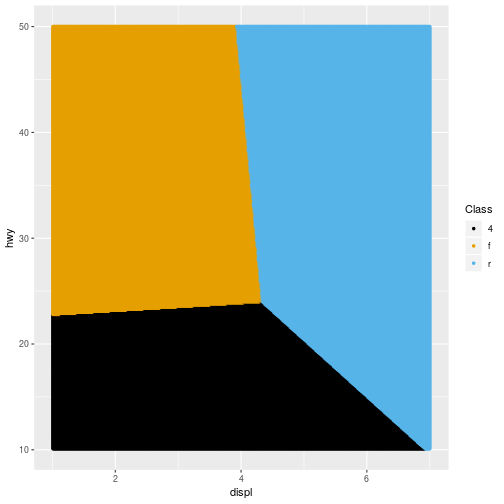
19
Multiclass Example: QDA
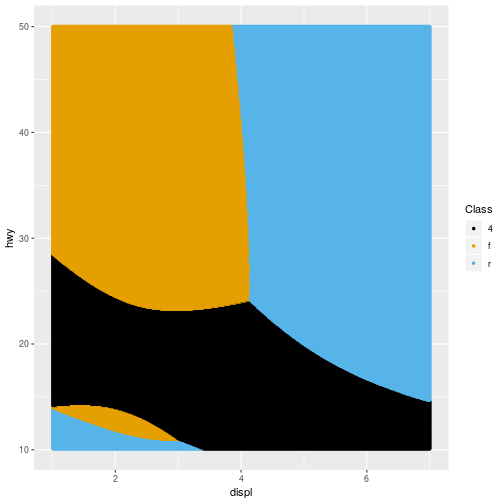
20
Are the assumptions valid?
21
Data again
22
As density
23
All assumptions hold
24
Different Variances Covariances
25
Assumptions
- With more predictors we cannot visualise in this way.
26
Assumptions
- With more predictors we cannot visualise in this way.
- There are formal hypothesis tests than can be used.
26
Assumptions
- With more predictors we cannot visualise in this way.
- There are formal hypothesis tests than can be used.
- Non normal data can be transformed to be closer to normal.
26
Assumptions
- With more predictors we cannot visualise in this way.
- There are formal hypothesis tests than can be used.
- Non normal data can be transformed to be closer to normal.
- Despite all of this, LDA and QDA often perform well in practice even when assumptions are violated.
26
Stability of LDA
27
Low variability
- Compared to k-NN classification LDA and QDA have lower variability across different training data sets.
28
Low variability
- Compared to k-NN classification LDA and QDA have lower variability across different training data sets.
- The next few slides show the decision boundaries of LDA and QDA for different subsamples of training data.
28
Original Training Sample: LDA
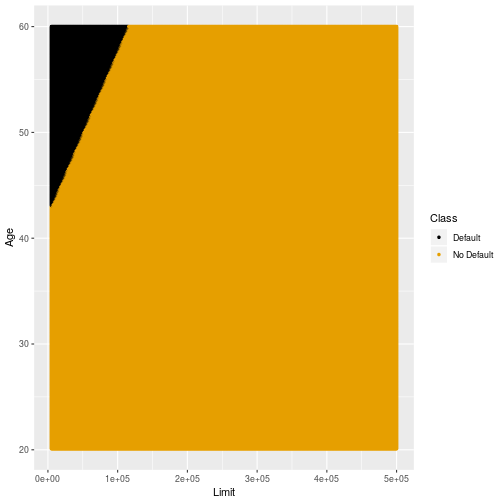
29
Different Training Sample LDA
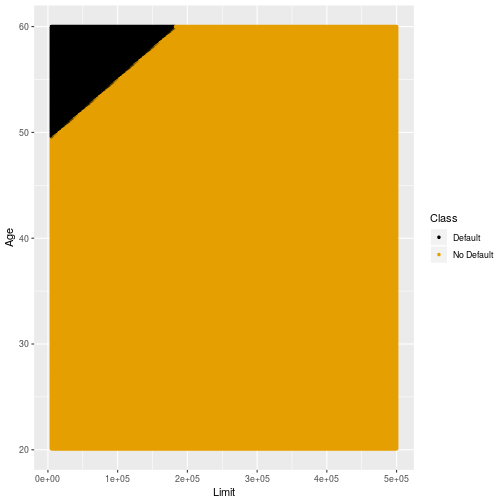
30
Original Training Sample: QDA
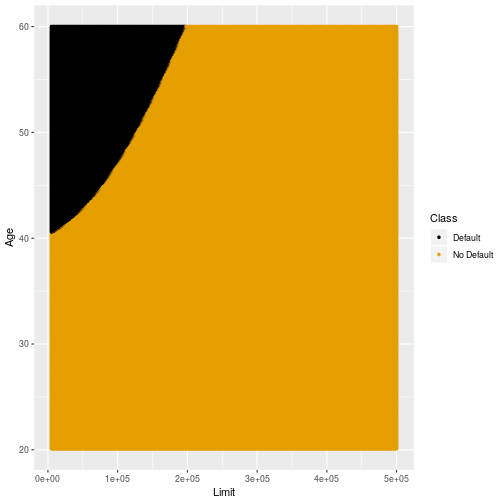
31
Different Training Sample QDA
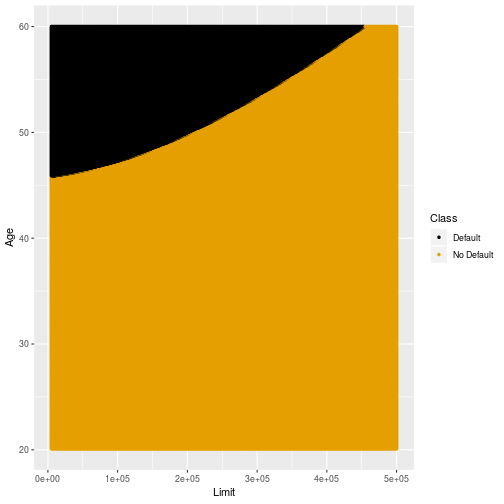
32
LDA and QDA in R
33
Package
- Discriminant Analysis can be implemented using the
MASSpackage.
34
Package
- Discriminant Analysis can be implemented using the
MASSpackage. - We will demonstrate using the
mpgdata.
34
Package
- Discriminant Analysis can be implemented using the
MASSpackage. - We will demonstrate using the
mpgdata. - We can split the data into training and test.
34
Package
- Discriminant Analysis can be implemented using the
MASSpackage. - We will demonstrate using the
mpgdata. - We can split the data into training and test.
- Carry out LDA and QDA on training data and form predictions for test data
34
Split Sample
#Find total number of observationsn<-NROW(mpg) #Create a vector allocating each observation to train #or testtrain_or_test<-ifelse(runif(n)<0.7,'Train','Test')#Add to mpg data framempg_exp<-add_column(mpg,Sample=train_or_test)#Isolate Training Data mpg_train<-filter(mpg_exp,Sample=='Train')#Isolate Test Data mpg_test<-filter(mpg_exp,Sample=='Test')35
Formulas in R
- To carry out discriminant Analysis we use the functions
ldaandqda.
36
Formulas in R
- To carry out discriminant Analysis we use the functions
ldaandqda. - These use the formula interface, the dependent variable is separated from the predictors using a
~. Between each dependent variable a+is included.
36
Formulas in R
- To carry out discriminant Analysis we use the functions
ldaandqda. - These use the formula interface, the dependent variable is separated from the predictors using a
~. Between each dependent variable a+is included. - The same syntax is used to do linear regression models in R.
36
Formulas in R
- To carry out discriminant Analysis we use the functions
ldaandqda. - These use the formula interface, the dependent variable is separated from the predictors using a
~. Between each dependent variable a+is included. - The same syntax is used to do linear regression models in R.
- Predictions for the test data can be obtained using the
predictfunction
36
LDA and QDA
#Linear Discriminant Analysislda_out<-lda(drv~displ+hwy,data = mpg_train)ldapred<-predict(lda_out,mpg_test)#Quadratic Discriminant Analysisqda_out<-qda(drv~displ+hwy,data = mpg_train)qdapred<-predict(qda_out,mpg_test)37
Missclasification Rate
The output of predict is a list and the element required is class. To compute test misclassification
mean(ldapred$class!=mpg_test$drv)## [1] 0.203125mean(qdapred$class!=mpg_test$drv)## [1] 0.17187538
Cross Tab
- It is also worth reporting results in a cross tabulation. For LDA
table(ldapred$class,mpg_test$drv)## ## 4 f r## 4 24 0 1## f 5 26 3## r 4 0 139
Additional features
- The probabilities are return in the
posteriorelement of the list returned by thepredictfunction.
ldapred$posterior## 4 f r## 1 0.0553215642 0.944421817 0.0002566191## 2 0.1278932882 0.871707586 0.0003991255## 3 0.3026359984 0.693399062 0.0039649393## 4 0.3026359984 0.693399062 0.0039649393## 5 0.3189705768 0.670590393 0.0104390298## 6 0.1961291816 0.005738036 0.7981327826## 7 0.1410847187 0.857422946 0.0014923354## 8 0.2332463929 0.754125971 0.0126276365## 9 0.4296848959 0.554664743 0.0156503607## 10 0.8743036767 0.116983213 0.0087131101## 11 0.7626457371 0.076606253 0.1607480098## 12 0.7626457371 0.076606253 0.1607480098## 13 0.9432843043 0.050391277 0.0063244190## 14 0.8932593617 0.037938000 0.0688026379## 15 0.8932593617 0.037938000 0.0688026379## 16 0.8077136327 0.019327340 0.1729590275## 17 0.9309438050 0.025709763 0.0433464322## 18 0.8932593617 0.037938000 0.0688026379## 19 0.9889679701 0.004882787 0.0061492426## 20 0.8733584374 0.013588920 0.1130526429## 21 0.4742213784 0.006036840 0.5197417820## 22 0.5928048694 0.020598933 0.3865961980## 23 0.9424996116 0.048926252 0.0085741364## 24 0.8713319435 0.106976631 0.0216914253## 25 0.8120982949 0.031648235 0.1562534698## 26 0.3336501591 0.573897236 0.0924526049## 27 0.2303238115 0.575307346 0.1943688428## 28 0.4229201507 0.446657823 0.1304220265## 29 0.0097899784 0.990025306 0.0001847160## 30 0.0149771330 0.984852041 0.0001708259## 31 0.0583817697 0.941119651 0.0004985793## 32 0.0285116707 0.969229936 0.0022583935## 33 0.2062382365 0.791972439 0.0017893249## 34 0.1177400450 0.850146358 0.0321135967## 35 0.0583817697 0.941119651 0.0004985793## 36 0.3938536285 0.603847461 0.0022989101## 37 0.6249386906 0.371731473 0.0033298362## 38 0.2671012145 0.013097099 0.7198016864## 39 0.4489201756 0.003508903 0.5475709211## 40 0.9065446043 0.068338938 0.0251164573## 41 0.8911146854 0.063432040 0.0454532747## 42 0.9424996116 0.048926252 0.0085741364## 43 0.0292904756 0.967561526 0.0031479988## 44 0.2459213102 0.708952565 0.0451261251## 45 0.3349540991 0.627890705 0.0371551958## 46 0.1175013514 0.735110167 0.1473884814## 47 0.1927344336 0.806596166 0.0006694001## 48 0.7843900809 0.214998514 0.0006114047## 49 0.8697092671 0.126821037 0.0034696961## 50 0.9406333346 0.057995334 0.0013713315## 51 0.8932593617 0.037938000 0.0688026379## 52 0.0285116707 0.969229936 0.0022583935## 53 0.0285116707 0.969229936 0.0022583935## 54 0.2289840756 0.761879396 0.0091365288## 55 0.0103599751 0.989280156 0.0003598685## 56 0.0044065043 0.995174630 0.0004188654## 57 0.9559271895 0.017166318 0.0269064922## 58 0.2671012145 0.013097099 0.7198016864## 59 0.9406333346 0.057995334 0.0013713315## 60 0.0583817697 0.941119651 0.0004985793## 61 0.4003583142 0.596470898 0.0031707878## 62 0.0583817697 0.941119651 0.0004985793## 63 0.0666381454 0.930744661 0.0026171932## 64 0.0003440082 0.998746778 0.000909213740
Exercises for you
- Evaluate whether the assumptions of multivariate normality and homogenous variances and covariances hold.
41
Exercises for you
- Evaluate whether the assumptions of multivariate normality and homogenous variances and covariances hold.
- Hints:
- For homogenous variances and covariances use
group_by,summarise,varandcov - For normality plot the data using
geom_density_2d()
- For homogenous variances and covariances use
41
Homogeneous Var-Cov
mpg_train%>% group_by(drv)%>% summarise(VarDispl=var(displ), VarHwy=var(hwy), covDisplHwy=cov(displ,hwy))->varcov## `summarise()` ungrouping output (override with `.groups` argument)| drv | VarDispl | VarHwy | covDisplHwy |
|---|---|---|---|
| 4 | 1.3713478 | 18.36957 | -4.0528986 |
| f | 0.5217152 | 18.47453 | -1.8201582 |
| r | 0.5125263 | 12.58947 | 0.2810526 |
42
Normality
mpg_train%>% ggplot(aes(x=displ,y=hwy,col=drv))+geom_density2d()+ scale_color_colorblind()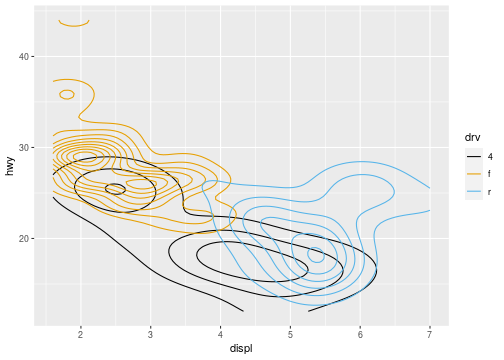
43
Other Linear Classifiers
44
Problem with LDA
- In LDA, the prediction is determined by some linear combination of the predictors
w0+w1x1+w0+…+wpxp
- The weights w depend in some complicated way on the variances and covariances of the predictors.
- All up there are p variances and (p2−p)/2 covariances that need to be estimated.
45
Large number of predictors
- Estimation is particularly difficult when p is large since the number of covariances that need to be estimated grows rapidly.
46
Large number of predictors
- Estimation is particularly difficult when p is large since the number of covariances that need to be estimated grows rapidly.
- A number of alternative methods exist to compute the weights.
46
Large number of predictors
- Estimation is particularly difficult when p is large since the number of covariances that need to be estimated grows rapidly.
- A number of alternative methods exist to compute the weights.
- The weights can be estimated using least squares for a two-class problem.
46
Large number of predictors
- Estimation is particularly difficult when p is large since the number of covariances that need to be estimated grows rapidly.
- A number of alternative methods exist to compute the weights.
- The weights can be estimated using least squares for a two-class problem.
- The weights can be estimated by assuming a probit or logit model and using maximum likelihood.
46
DA v Logistic Regression
- If the classes are well separated estimates from logistic regression tend to be unstable.
47
DA v Logistic Regression
- If the classes are well separated estimates from logistic regression tend to be unstable.
- If there are a small number of observations, estimates from logistic regression tend to be unstable.
47
DA v Logistic Regression
- If the classes are well separated estimates from logistic regression tend to be unstable.
- If there are a small number of observations, estimates from logistic regression tend to be unstable.
- Logistic regression is covered in detail in ETF3600.
47
Naive Bayes
- Another alternative is to apply Bayes method but to assume the predictors are independent.
48
Naive Bayes
- Another alternative is to apply Bayes method but to assume the predictors are independent.
- In this case there is no need to estimate covariances.
48
Naive Bayes
- Another alternative is to apply Bayes method but to assume the predictors are independent.
- In this case there is no need to estimate covariances.
- Since the assumption of independence rarely holds this is known as naive Bayes.
48
Naive Bayes
- Another alternative is to apply Bayes method but to assume the predictors are independent.
- In this case there is no need to estimate covariances.
- Since the assumption of independence rarely holds this is known as naive Bayes.
- For naive Bayes it is easier to move away from the assumption of normality
48
Naive Bayes
- Another alternative is to apply Bayes method but to assume the predictors are independent.
- In this case there is no need to estimate covariances.
- Since the assumption of independence rarely holds this is known as naive Bayes.
- For naive Bayes it is easier to move away from the assumption of normality
- Doing so may lead to a non linear classifier.
48
Conclusion
- The Bayesian method gives a theoretically optimal solution to the classification problem.
49
Conclusion
- The Bayesian method gives a theoretically optimal solution to the classification problem.
- In practice however assumptions need to be made that may not hold in reality.
49
Conclusion
- The Bayesian method gives a theoretically optimal solution to the classification problem.
- In practice however assumptions need to be made that may not hold in reality.
- An advantage of LDA (and QDA) is that they are more stable and will not vary too much when different training samples are used.
49
Conclusion
- The Bayesian method gives a theoretically optimal solution to the classification problem.
- In practice however assumptions need to be made that may not hold in reality.
- An advantage of LDA (and QDA) is that they are more stable and will not vary too much when different training samples are used.
- Another advantage of LDA is interpretability.
49
Conclusion
- The Bayesian method gives a theoretically optimal solution to the classification problem.
- In practice however assumptions need to be made that may not hold in reality.
- An advantage of LDA (and QDA) is that they are more stable and will not vary too much when different training samples are used.
- Another advantage of LDA is interpretability.
- A disadvantage of LDA and QDA is that they are too simple for complicated decision boundaries.
49