Decision Trees
Data Visualisation and Analytics
Anastasios Panagiotelis and Lauren Kennedy
Lecture 11
1
Trees
2
Credit Data
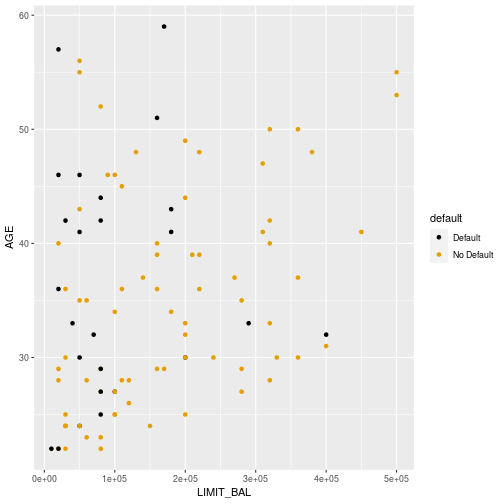
3
Default or not?
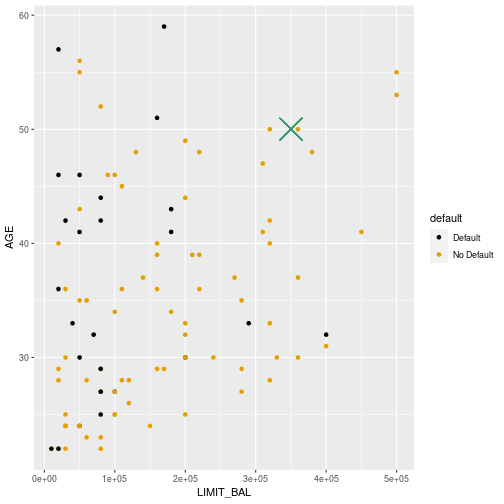
4
Default or not?
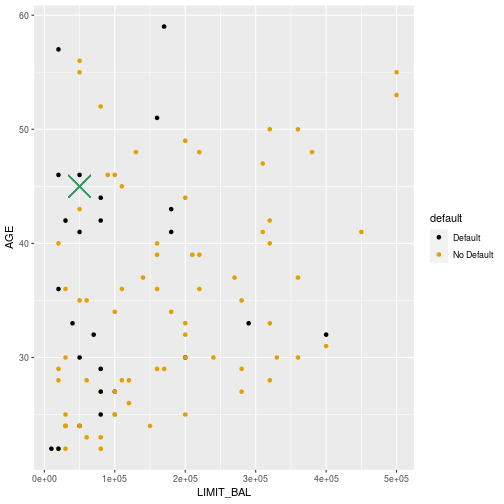
5
A tree
Predict default or no default for
6
A tree
Predict default or no default for
- 45 year old with a limit of 100000
- 45 year old with a limit of 50000
- 35 year old with a limit of 50000
6
A tree
Predict default or no default for
- 45 year old with a limit of 100000
- 45 year old with a limit of 50000
- 35 year old with a limit of 50000
Using the information on the next slide
6
Decision tree
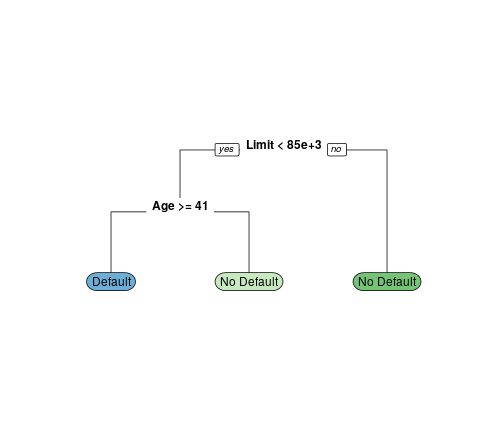
7
Basic terminology
- Every line is called an edge or a branch. They are connected to nodes.
8
Basic terminology
- Every line is called an edge or a branch. They are connected to nodes.
- At the nodes a rule determines which branch to take to the next node.
8
Basic terminology
- Every line is called an edge or a branch. They are connected to nodes.
- At the nodes a rule determines which branch to take to the next node.
- Nodes at the bottom are called terminal nodes or leaves.
8
Basic terminology
- Every line is called an edge or a branch. They are connected to nodes.
- At the nodes a rule determines which branch to take to the next node.
- Nodes at the bottom are called terminal nodes or leaves.
- At the leaves a decision is made on how to classify the variable.
8
Basic terminology
- Every line is called an edge or a branch. They are connected to nodes.
- At the nodes a rule determines which branch to take to the next node.
- Nodes at the bottom are called terminal nodes or leaves.
- At the leaves a decision is made on how to classify the variable.
- Note that the tree is upside down!
8
Partitioning
If xj is a single predictor, then rules that determine each decision have the following form
If xj>c then go to one nodeIf xj≤c then go to the other node
This is called binary splitting
9
Partition
- Each leaf corresponds to a box of values for the predictors.
10
Partition
- Each leaf corresponds to a box of values for the predictors.
- Each of these boxes contains a few training observations.
10
Partition
- Each leaf corresponds to a box of values for the predictors.
- Each of these boxes contains a few training observations.
- Within each box find the most frequent class amongst these training observations.
10
Partition
- Each leaf corresponds to a box of values for the predictors.
- Each of these boxes contains a few training observations.
- Within each box find the most frequent class amongst these training observations.
- This yields the predicted class for each box.
10
Partition
- Each leaf corresponds to a box of values for the predictors.
- Each of these boxes contains a few training observations.
- Within each box find the most frequent class amongst these training observations.
- This yields the predicted class for each box.
- This will be clearer when we look at decision boundaries.
10
How to split?
- The challenge is to find an xj and c to make each split.
11
How to split?
- The challenge is to find an xj and c to make each split.
- One way is to define some criteria of best split
11
How to split?
- The challenge is to find an xj and c to make each split.
- One way is to define some criteria of best split
- Then try all combinations of xj and c.
11
How to split?
- The challenge is to find an xj and c to make each split.
- One way is to define some criteria of best split
- Then try all combinations of xj and c.
- For continuous xj, simply rank the xj from smallest to largest.
- Then consider the midpoints between consecutive values of xj
11
Simple example first split
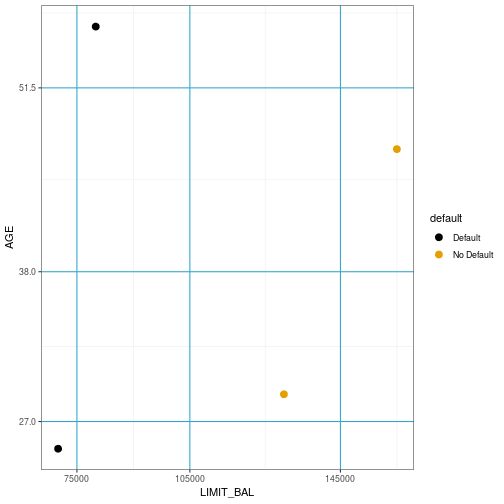
12
What is a good split?
- There are multiple ways of thinking about a good split.
13
What is a good split?
- There are multiple ways of thinking about a good split.
- One is to think in terms of misclassification error.
13
What is a good split?
- There are multiple ways of thinking about a good split.
- One is to think in terms of misclassification error.
- Another set of measures aim for the partition to be pure.
13
What is a good split?
- There are multiple ways of thinking about a good split.
- One is to think in terms of misclassification error.
- Another set of measures aim for the partition to be pure.
- By purity we mean than as most observations within a partition belong to the same class.
13
Gini Impurity
- Let pmk be the proportion of training observations in partition m in class k and K be the total number of classes.
G=K∑k=1pmk(1−pmk)
- In the two class case maximised when half of the observations are in each class
- Minimised when all observations are in a single class.
14
Perfect split
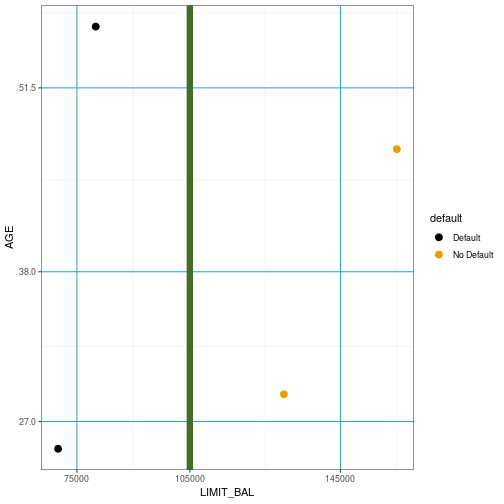
15
Worst split
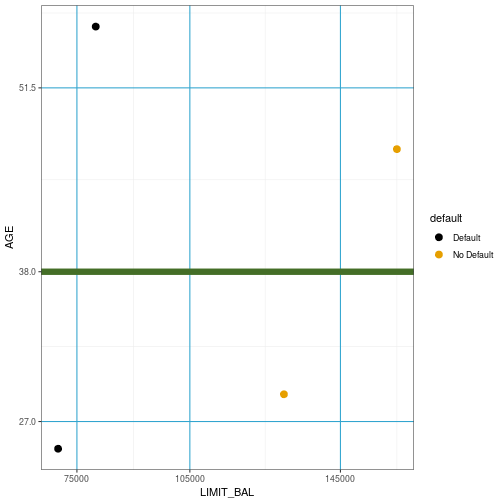
16
Not best or worst
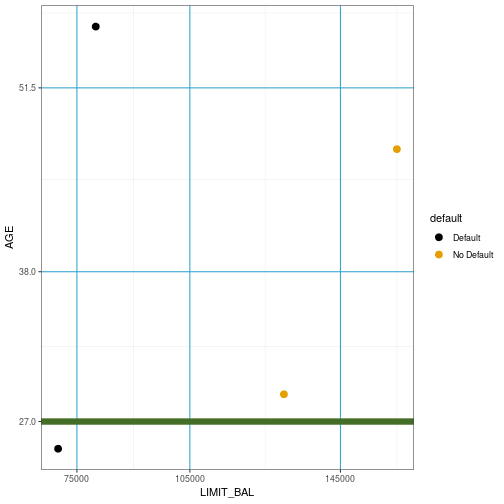
17
Exercise
- In the last plot calculate the Gini impurity for both partitions.
18
Exercise
- In the last plot calculate the Gini impurity for both partitions.
- For the bottom, Gini Impurity is 0
18
Exercise
- In the last plot calculate the Gini impurity for both partitions.
- For the bottom, Gini Impurity is 0
- For the top 1323+2313=49
18
Stopping
19
When to stop
- In principle a tree can be grown so that every training observation is in its own partition.
20
When to stop
- In principle a tree can be grown so that every training observation is in its own partition.
- In this case the in sample fit will be perfect
20
When to stop
- In principle a tree can be grown so that every training observation is in its own partition.
- In this case the in sample fit will be perfect
- This does not work well for out of sample prediction.
20
Control
- The complexity of the tree can be controlled in a number of ways:
21
Control
- The complexity of the tree can be controlled in a number of ways:
- Set a maximum depth of tree.
- Set a minimum number of training observations in each partition.
- Only accept a split that improves the criterion by a fixed amount.
- Pruning
21
Pruning
- The idea behind pruning is to start with a large tree.
22
Pruning
- The idea behind pruning is to start with a large tree.
- A new objective function is defined that penalises larger trees.
22
Pruning
- The idea behind pruning is to start with a large tree.
- A new objective function is defined that penalises larger trees.
- Consider different sub trees of the large tree that optimise the penalised objective.
22
Pruning
- The idea behind pruning is to start with a large tree.
- A new objective function is defined that penalises larger trees.
- Consider different sub trees of the large tree that optimise the penalised objective.
- There is a tuning parameter that can be set by CV.
22
Decision Boundary
23
Data again
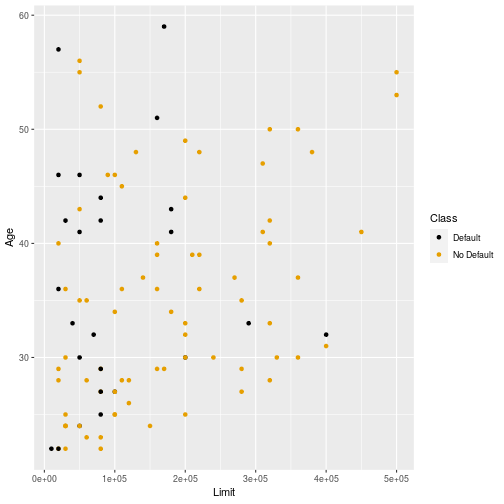
24
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN and DA is presented again.
25
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN and DA is presented again.
- If the tree predicts "Default" the grid point is colored black.
25
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN and DA is presented again.
- If the tree predicts "Default" the grid point is colored black.
- If the tree predicts "No default" the grid point is colored yellow.
25
Decision Boundaries
- For the next few slides the same grid of points that was used for kNN and DA is presented again.
- If the tree predicts "Default" the grid point is colored black.
- If the tree predicts "No default" the grid point is colored yellow.
- Think about how these decision boundaries compare to kNN and DA.
25
Decision Boundary: Biggest Tree
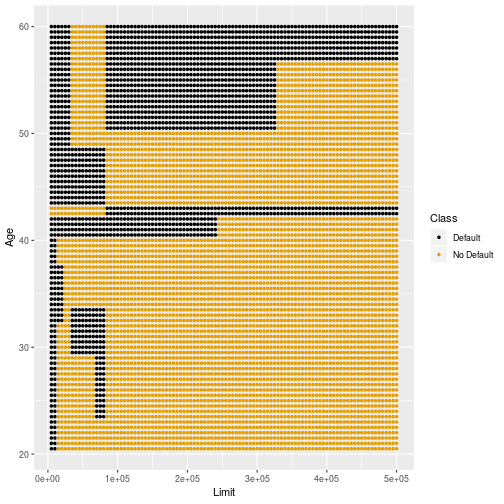
26
Decision Tree: Biggest Tree
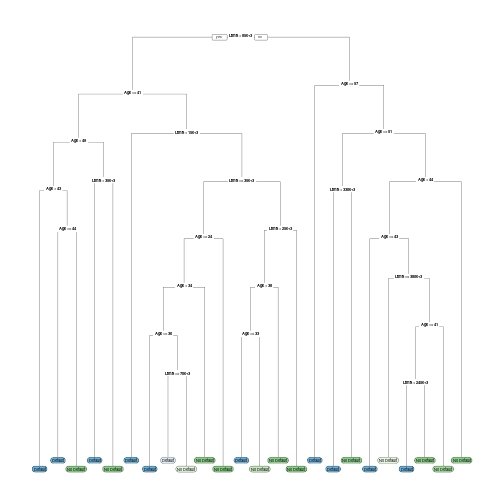
27
Controls
- This tree is too complicated and will overfit the data.
28
Controls
- This tree is too complicated and will overfit the data.
- Build a smaller tree using defaults of the R function.
28
Controls
- This tree is too complicated and will overfit the data.
- Build a smaller tree using defaults of the R function.
- There must be at least 7 observations in a partition.
28
Controls
- This tree is too complicated and will overfit the data.
- Build a smaller tree using defaults of the R function.
- There must be at least 7 observations in a partition.
- If a split does not improve Gini Impurity by more than 0.01 the algorithm stops.
28
Decision Boundary: Smaller Tree
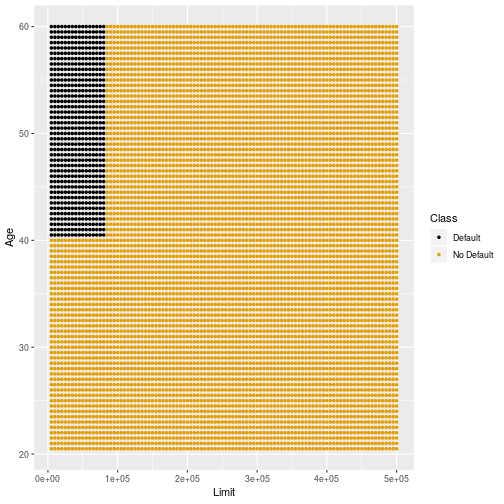
29
Multiclass Example
- On the next few slides we will consider a different dataset where the target variable can take three values.
30
Multiclass Example
- On the next few slides we will consider a different dataset where the target variable can take three values.
- Using the
mpgdataset we will predict whether a car is a 4wd, a rear wheel drive or a front wheel drive.
30
Multiclass Example
- On the next few slides we will consider a different dataset where the target variable can take three values.
- Using the
mpgdataset we will predict whether a car is a 4wd, a rear wheel drive or a front wheel drive. - The predictors will be fuel efficiency on the highway (
hwy) and engine size (displ)
30
Multiclass Example: Data
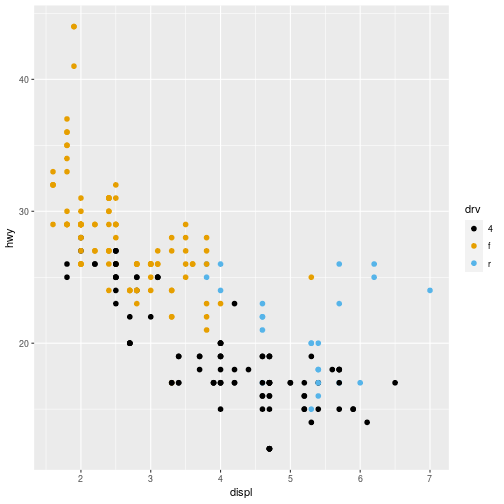
31
Multiclass Example: Tree
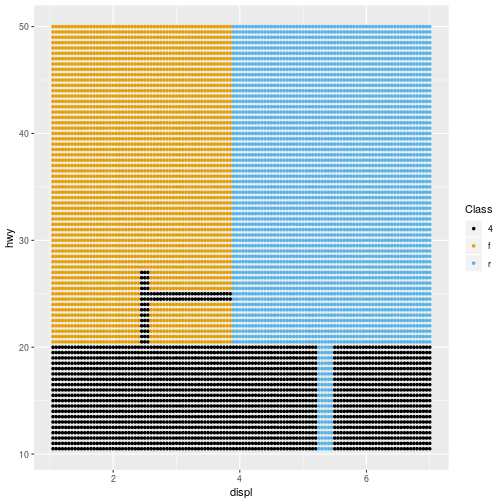
32
Decision Tree: Multiclass
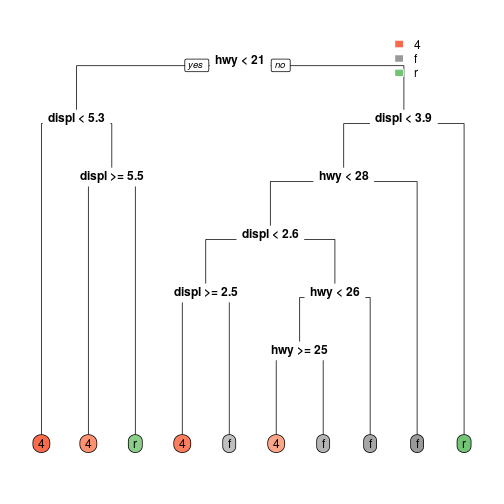
33
Stability of Trees
34
Low variability
- Compared to LDA and QDA, trees have higher variability across different training data sets.
35
Low variability
- Compared to LDA and QDA, trees have higher variability across different training data sets.
- This can be mitigated by choosing smaller trees.
35
Low variability
- Compared to LDA and QDA, trees have higher variability across different training data sets.
- This can be mitigated by choosing smaller trees.
- The next few slides show the decision boundaries of trees for different subsamples of training data.
35
Train Sample 1: Big Tree
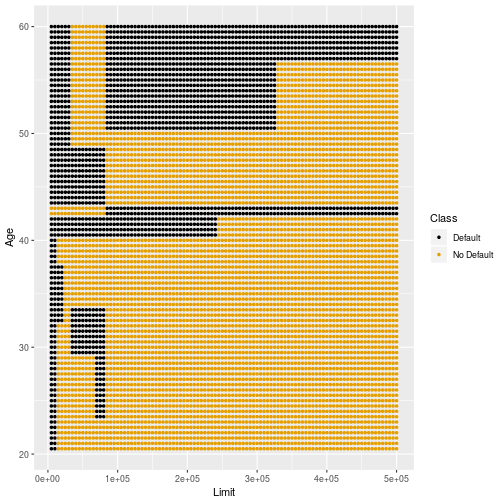
36
Train Sample 2: Big Tree
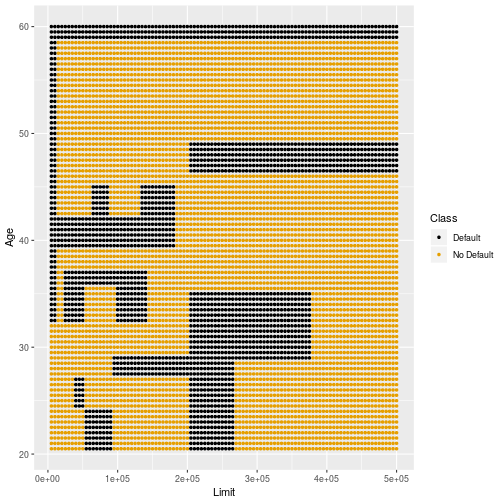
37
Train Sample 1: Small Tree
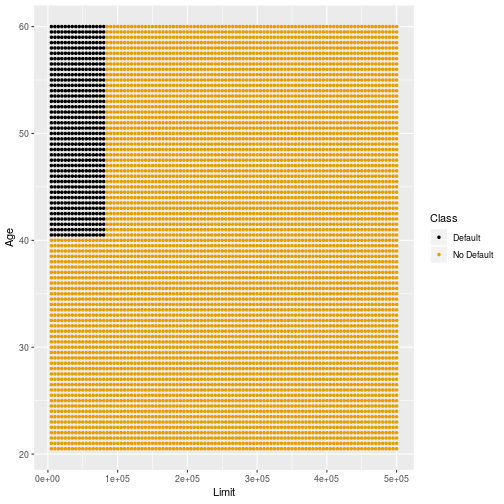
38
Train Sample 2: Small Tree

39
Trees in R
40
Package
- Classification trees can be implemented using the
rpartpackage.
41
Package
- Classification trees can be implemented using the
rpartpackage. - We will demonstrate using the
mpgdata.
41
Package
- Classification trees can be implemented using the
rpartpackage. - We will demonstrate using the
mpgdata. - Like last week split the data into training and test.
41
Package
- Classification trees can be implemented using the
rpartpackage. - We will demonstrate using the
mpgdata. - Like last week split the data into training and test.
- Find a decision tree on the training data and form predictions for test data
41
Split Sample
#Find total number of observationsn<-NROW(mpg) #Create a vector allocating each observation to train #or testtrain_or_test<-ifelse(runif(n)<0.7,'Train','Test')#Add to mpg data framempg_exp<-add_column(mpg,Sample=train_or_test)#Isolate Training Data mpg_train<-filter(mpg_exp,Sample=='Train')#Isolate Test Data mpg_test<-filter(mpg_exp,Sample=='Test')42
Tree
#Default Settingsrpart_small<-rpart(drv~displ+hwy,data = mpg_train)#Bigger tree#Allow for partitions with as few as two #training observations#Accept any split that improves fitrpart_big<-rpart(drv~displ+hwy,data = mpg_train, control = rpart.control(minbucket=2, cp=0))#Make predictionspred_small<-predict(rpart_small,mpg_test,type='class')pred_big<-predict(rpart_big,mpg_test,type='class')43
Missclasification Rate
To compute test misclassification
mean(pred_small!=mpg_test$drv)## [1] 0.15625mean(pred_big!=mpg_test$drv)## [1] 0.14062544
Missclasification Rate
To compute test misclassification
mean(pred_small!=mpg_test$drv)## [1] 0.15625mean(pred_big!=mpg_test$drv)## [1] 0.140625In the bigger tree perform better out-of-sample (this is rare).
44
Probabilities
- By leaving out the
type='class'option probabilities are returned
45
Probabilities
- By leaving out the
type='class'option probabilities are returned - These probabilities are simply the proportions of the classes within each partition.
45
Probabilities
- By leaving out the
type='class'option probabilities are returned - These probabilities are simply the proportions of the classes within each partition.
pred_small<-predict(rpart_small,mpg_test)pred_small## 4 f r## 1 0.0000000 1.00000000 0.00000000## 2 0.1315789 0.81578947 0.05263158## 3 0.1315789 0.81578947 0.05263158## 4 0.1315789 0.81578947 0.05263158## 5 0.1315789 0.81578947 0.05263158## 6 0.0000000 0.00000000 1.00000000## 7 0.0000000 1.00000000 0.00000000## 8 0.0000000 1.00000000 0.00000000## 9 0.1315789 0.81578947 0.05263158## 10 0.9743590 0.02564103 0.00000000## 11 0.9743590 0.02564103 0.00000000## 12 0.9743590 0.02564103 0.00000000## 13 0.9743590 0.02564103 0.00000000## 14 0.9743590 0.02564103 0.00000000## 15 0.9743590 0.02564103 0.00000000## 16 0.7777778 0.00000000 0.22222222## 17 0.9743590 0.02564103 0.00000000## 18 0.9743590 0.02564103 0.00000000## 19 0.9743590 0.02564103 0.00000000## 20 0.9743590 0.02564103 0.00000000## 21 0.9743590 0.02564103 0.00000000## 22 0.3333333 0.00000000 0.66666667## 23 0.9743590 0.02564103 0.00000000## 24 0.9743590 0.02564103 0.00000000## 25 0.9743590 0.02564103 0.00000000## 26 0.1315789 0.81578947 0.05263158## 27 0.1315789 0.81578947 0.05263158## 28 0.0000000 0.00000000 1.00000000## 29 0.0000000 1.00000000 0.00000000## 30 0.0000000 1.00000000 0.00000000## 31 0.3125000 0.68750000 0.00000000## 32 0.8571429 0.14285714 0.00000000## 33 0.1315789 0.81578947 0.05263158## 34 0.3125000 0.68750000 0.00000000## 35 0.3125000 0.68750000 0.00000000## 36 0.1315789 0.81578947 0.05263158## 37 0.9743590 0.02564103 0.00000000## 38 0.7777778 0.00000000 0.22222222## 39 0.9743590 0.02564103 0.00000000## 40 0.9743590 0.02564103 0.00000000## 41 0.9743590 0.02564103 0.00000000## 42 0.9743590 0.02564103 0.00000000## 43 0.0000000 1.00000000 0.00000000## 44 0.1315789 0.81578947 0.05263158## 45 0.9743590 0.02564103 0.00000000## 46 0.0000000 0.00000000 1.00000000## 47 0.3125000 0.68750000 0.00000000## 48 0.9743590 0.02564103 0.00000000## 49 0.9743590 0.02564103 0.00000000## 50 0.9743590 0.02564103 0.00000000## 51 0.0000000 1.00000000 0.00000000## 52 0.0000000 1.00000000 0.00000000## 53 0.1315789 0.81578947 0.05263158## 54 0.1315789 0.81578947 0.05263158## 55 0.0000000 1.00000000 0.00000000## 56 0.0000000 1.00000000 0.00000000## 57 0.7777778 0.00000000 0.22222222## 58 0.9743590 0.02564103 0.00000000## 59 0.9743590 0.02564103 0.00000000## 60 0.1315789 0.81578947 0.05263158## 61 0.0000000 1.00000000 0.00000000## 62 0.0000000 1.00000000 0.00000000## 63 0.1315789 0.81578947 0.05263158## 64 0.0000000 1.00000000 0.0000000045
Plotting the trees
- The pacakge
rpart.plotis good for plotting trees themselves. - The trees we have plot so far use code such as that below.
rpart.plot(rpart_small,extra = 0,type = 0)rpart.plot(rpart_small,extra = 0,type = 0)46
Small Tree
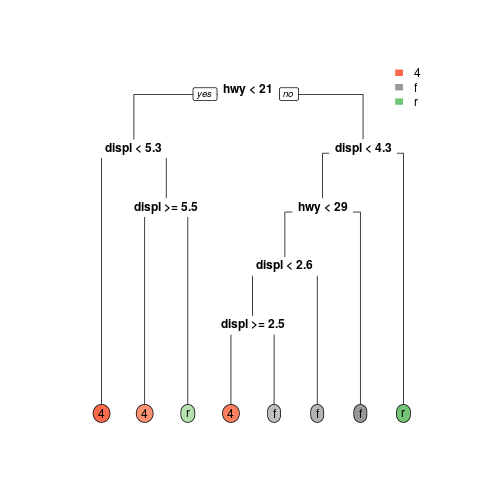
47
Big Tree
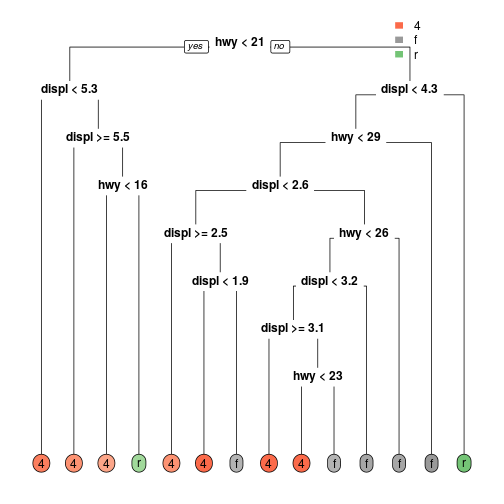
48
More detail
- By default, the function
rpart.plotactually provides more information. Try the following
49
More detail
- By default, the function
rpart.plotactually provides more information. Try the following
rpart.plot(rpart_small)49
More detail
- By default, the function
rpart.plotactually provides more information. Try the following
rpart.plot(rpart_small)- This provides
49
More detail
- By default, the function
rpart.plotactually provides more information. Try the following
rpart.plot(rpart_small)- This provides
- The most frequent class in each split
- The proportion of all classes in each split
- The proportion of data in each split
49
Small Tree
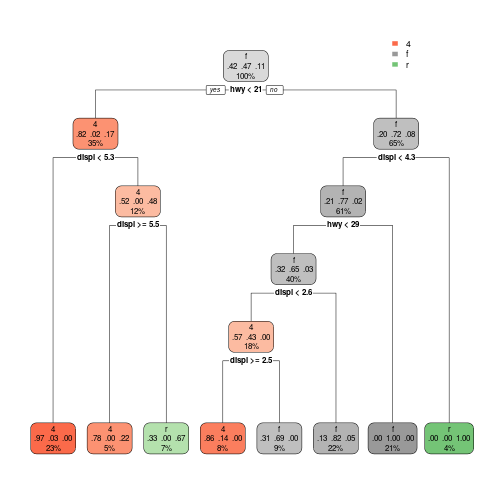
50
Regression Trees
- The same ideas can be applied to regression.
51
Regression Trees
- The same ideas can be applied to regression.
- The prediction is the average value of the dependent variable for all training observations in the same partition.
51
Regression Trees
- The same ideas can be applied to regression.
- The prediction is the average value of the dependent variable for all training observations in the same partition.
- Splits can be chosen to minimise sum of squared errors rather than Gini impurity.
51
Ensemble methods
- Due to their high variablity ensemble methods are often used together with trees.
52
Ensemble methods
- Due to their high variablity ensemble methods are often used together with trees.
- One way to do this is to resample the data many times and fit a new tree each time (bagging).
52
Ensemble methods
- Due to their high variablity ensemble methods are often used together with trees.
- One way to do this is to resample the data many times and fit a new tree each time (bagging).
- When the number of predictors is large these can also be randomly sampled (random forest).
52
Ensemble methods
- Due to their high variablity ensemble methods are often used together with trees.
- One way to do this is to resample the data many times and fit a new tree each time (bagging).
- When the number of predictors is large these can also be randomly sampled (random forest).
- A prediction is obtained from each tree, and the prediction will be the most frequent class across trees.
52
Conclusion
- Classification trees are a very intuitive and interpretable way that allow for data to guide decision making.
53
Conclusion
- Classification trees are a very intuitive and interpretable way that allow for data to guide decision making.
- In practice much care must be taken to prevent overfitting.
53
Conclusion
- Classification trees are a very intuitive and interpretable way that allow for data to guide decision making.
- In practice much care must be taken to prevent overfitting.
- Even so, trees are very sensitive to small changes in training data.
53
Conclusion
- Classification trees are a very intuitive and interpretable way that allow for data to guide decision making.
- In practice much care must be taken to prevent overfitting.
- Even so, trees are very sensitive to small changes in training data.
- As such, trees are usually combined in more sophisticated ensemble learning methods.
53
Conclusion
- Classification trees are a very intuitive and interpretable way that allow for data to guide decision making.
- In practice much care must be taken to prevent overfitting.
- Even so, trees are very sensitive to small changes in training data.
- As such, trees are usually combined in more sophisticated ensemble learning methods.
- This does come at the cost of interpretability.
53