+ - 0:00:00
Notes for current slide
Notes for next slide

Introduction and Motivation

High Dimensional Data Analysis

Anastasios Panagiotelis & Ruben Loaiza-Maya

Lecture 1

1

A Data Story

2

High-Dimensional Data?

  • First what do we mean by High Dimensional?
  • The data we look at will have:
    • Observations
    • Variables
  • Generally High Dimensional implies that the number of variables is large.
3

High-Dimensional Data?

  • First what do we mean by High Dimensional?
  • The data we look at will have:
    • Observations
    • Variables
  • Generally High Dimensional implies that the number of variables is large.
  • The term, high-dimensional also relates thinking about and visualising data as points in space.
3

US States

  • Five indicators of the quality of life in the 50 States of the USA in 1977.
    • Income,
    • Illiteracy rate,
    • High school graduation rate,
    • Life expectancy,
    • Murder rates.
  • Let's explore!
4

A dataset

State Income Illiteracy LifeExp Murder HSGrad StateAbb
Alabama 3624 2.1 69.05 15.1 41.3 AL
Alaska 6315 1.5 69.31 11.3 66.7 AK
Arizona 4530 1.8 70.55 7.8 58.1 AZ
Arkansas 3378 1.9 70.66 10.1 39.9 AR
California 5114 1.1 71.71 10.3 62.6 CA
Colorado 4884 0.7 72.06 6.8 63.9 CO
Connecticut 5348 1.1 72.48 3.1 56.0 CT
Delaware 4809 0.9 70.06 6.2 54.6 DE
Florida 4815 1.3 70.66 10.7 52.6 FL
Georgia 4091 2.0 68.54 13.9 40.6 GA
Hawaii 4963 1.9 73.60 6.2 61.9 HI
Idaho 4119 0.6 71.87 5.3 59.5 ID
Illinois 5107 0.9 70.14 10.3 52.6 IL
Indiana 4458 0.7 70.88 7.1 52.9 IN
Iowa 4628 0.5 72.56 2.3 59.0 IA
Kansas 4669 0.6 72.58 4.5 59.9 KS
Kentucky 3712 1.6 70.10 10.6 38.5 KY
Louisiana 3545 2.8 68.76 13.2 42.2 LA
Maine 3694 0.7 70.39 2.7 54.7 ME
Maryland 5299 0.9 70.22 8.5 52.3 MD
Massachusetts 4755 1.1 71.83 3.3 58.5 MA
Michigan 4751 0.9 70.63 11.1 52.8 MI
Minnesota 4675 0.6 72.96 2.3 57.6 MN
Mississippi 3098 2.4 68.09 12.5 41.0 MS
Missouri 4254 0.8 70.69 9.3 48.8 MO
Montana 4347 0.6 70.56 5.0 59.2 MT
Nebraska 4508 0.6 72.60 2.9 59.3 NE
Nevada 5149 0.5 69.03 11.5 65.2 NV
New Hampshire 4281 0.7 71.23 3.3 57.6 NH
New Jersey 5237 1.1 70.93 5.2 52.5 NJ
New Mexico 3601 2.2 70.32 9.7 55.2 NM
New York 4903 1.4 70.55 10.9 52.7 NY
North Carolina 3875 1.8 69.21 11.1 38.5 NC
North Dakota 5087 0.8 72.78 1.4 50.3 ND
Ohio 4561 0.8 70.82 7.4 53.2 OH
Oklahoma 3983 1.1 71.42 6.4 51.6 OK
Oregon 4660 0.6 72.13 4.2 60.0 OR
Pennsylvania 4449 1.0 70.43 6.1 50.2 PA
Rhode Island 4558 1.3 71.90 2.4 46.4 RI
South Carolina 3635 2.3 67.96 11.6 37.8 SC
South Dakota 4167 0.5 72.08 1.7 53.3 SD
Tennessee 3821 1.7 70.11 11.0 41.8 TN
Texas 4188 2.2 70.90 12.2 47.4 TX
Utah 4022 0.6 72.90 4.5 67.3 UT
Vermont 3907 0.6 71.64 5.5 57.1 VT
Virginia 4701 1.4 70.08 9.5 47.8 VA
Washington 4864 0.6 71.72 4.3 63.5 WA
West Virginia 3617 1.4 69.48 6.7 41.6 WV
Wisconsin 4468 0.7 72.48 3.0 54.5 WI
Wyoming 4566 0.6 70.29 6.9 62.9 WY
5

Observations and Variables

On the previous slide and in general:

  • Each row corresponds to an observation
    • In this example that is a State.
  • Each column corresponds to a variable
    • In this example that is an attribute of each State.
6

Histogram: Income

7

Scatter-plot: Income v Mortality

8

3D Scatter-plot

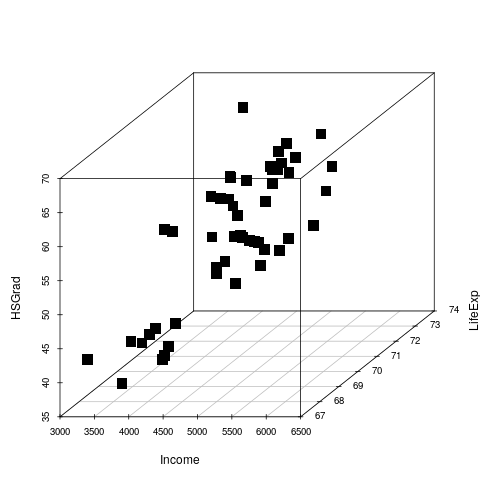
9

3D Scatter-plot

Click and drag to rotate

You must enable Javascript to view this page properly.

10

Lessons learnt

  • With 2 variables we can do a 2-dimensional (2D) scatter plot.
    • This can be interpreted very easily
  • With 3 variables we can do a 3D scatter plot
    • This doesn't look great on a flat screen
    • We get more insight by rotating the plot
  • What about 5 variables? What about 100 variables?
11

Principal components

  • Later on we will cover the method of principal components.
12

Principal components

  • Later on we will cover the method of principal components.
  • This can be used to combine the variables into a single index.
12

Principal components

  • Later on we will cover the method of principal components.
  • This can be used to combine the variables into a single index.
  • This single index explains most of the variation in the data.
12

Principal components

  • Later on we will cover the method of principal components.
  • This can be used to combine the variables into a single index.
  • This single index explains most of the variation in the data.
  • On the next slide we plot the first principal component on a map of the USA.
12

One PC on a map

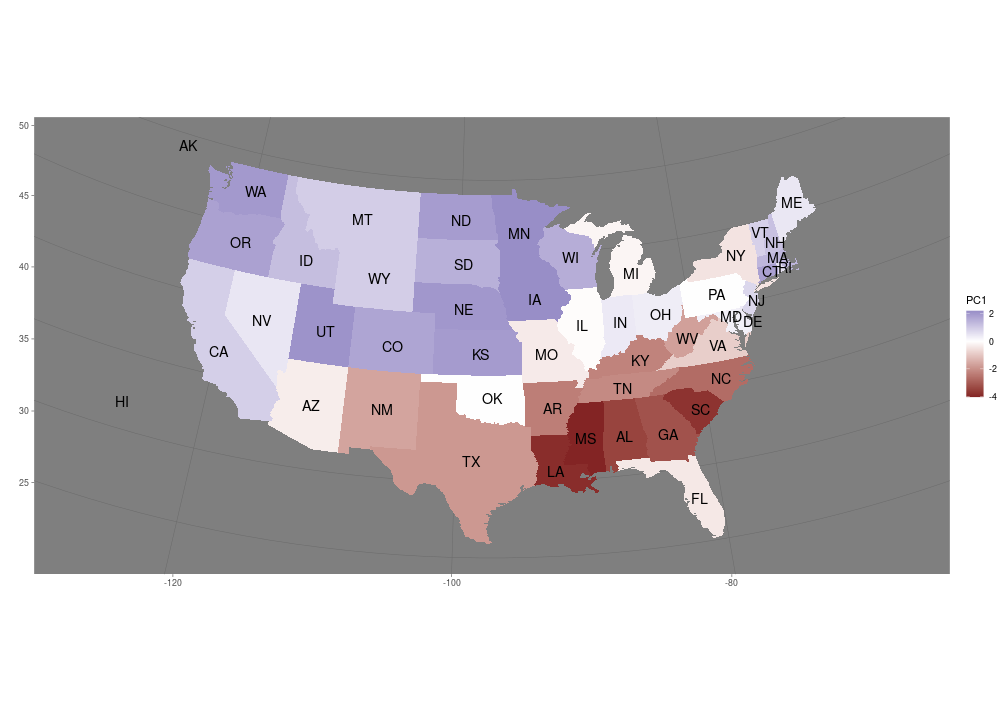
13

Multidimensional Scaling

  • Two states close to one another on the scatterplot had similar levels of income, and life expectancy.
14

Multidimensional Scaling

  • Two states close to one another on the scatterplot had similar levels of income, and life expectancy.
  • Can we do something similar but for all five variables.
14

Multidimensional Scaling

  • Two states close to one another on the scatterplot had similar levels of income, and life expectancy.
  • Can we do something similar but for all five variables.
  • The method of multidimensional scaling finds two coordinates so that states close to one another on the scatterplot are close to one another across all five characteristics.
14

Multidimensional Scaling

15

Factor Analysis

  • Later on we will attempt to attach possible interpretations to these constructed variables.
16

Factor Analysis

  • Later on we will attempt to attach possible interpretations to these constructed variables.
  • This is the objective of factor modelling.
16

Factor Analysis

  • Later on we will attempt to attach possible interpretations to these constructed variables.
  • This is the objective of factor modelling.
  • In this context factor refers to a latent construct that cannot be directly observed but can be measured via its correlation with observable data.
16

Cluster Analysis

  • Even from the simple analysis so far, it appears that similar states can placed into a small number of groups.
17

Cluster Analysis

  • Even from the simple analysis so far, it appears that similar states can placed into a small number of groups.
  • The use of algorithms that achieve this task is known as cluster analysis.
17

Cluster Analysis

  • Even from the simple analysis so far, it appears that similar states can placed into a small number of groups.
  • The use of algorithms that achieve this task is known as cluster analysis.
  • It is extremely useful across a number of business disciplines.
17

Cluster Analysis

  • Even from the simple analysis so far, it appears that similar states can placed into a small number of groups.
  • The use of algorithms that achieve this task is known as cluster analysis.
  • It is extremely useful across a number of business disciplines.
  • On the following slide we group the states into two clusters and present them in different colors.
17

Cluster Analysis: Example

18

A broad understanding of data.

19

Numerical Data

  • So far we looked at numerical data
    • This is also called metric data or ratio data
  • The differences and ratios between values of the variable have some meaningful interpretation.
20

Numerical Data

  • So far we looked at numerical data
    • This is also called metric data or ratio data
  • The differences and ratios between values of the variable have some meaningful interpretation.
  • A state with a mean income of $5000 has twice as much income as a state with a mean income of $2500.
20

Non-metric data

  • Categorical (or nominal) Data
    • The value of the variable does not measure the size of some characteristic.
  • Ordinal data
    • Different values of the variable measure more or less of a characteristic but not how much more or how much less.
21

Beer Data

beer rating origin avail price cost calories sodium alcohol light
Budweiser Light Good USA National 2.63 0.44 113 8 3.7 LIGHT
Coors Light Good USA Regional 2.73 0.46 102 15 4.1 LIGHT
Michelob Light Good USA National 2.99 0.50 135 11 4.2 LIGHT
Miller Light Good USA National 2.55 0.43 99 10 4.3 LIGHT
Olympia Gold Light Fair USA Regional 2.75 0.46 72 6 2.9 LIGHT
Pabst Extra Light Fair USA National 2.29 0.38 68 15 2.3 LIGHT
Schlitz Light Fair USA National 2.79 0.47 97 7 4.2 LIGHT
Anchor Steam VeryGood USA Regional 7.19 1.20 154 17 4.7 NONLIGHT
Augsberger Good USA Regional 2.39 0.40 175 24 5.5 NONLIGHT
Becks Good Germany Regional 4.55 0.76 150 19 4.7 NONLIGHT
Blatz Fair USA Regional 1.79 0.30 144 13 4.6 NONLIGHT
Budweiser VeryGood USA National 2.59 0.43 144 15 4.7 NONLIGHT
Coors Good USA Regional 2.65 0.44 140 18 4.6 NONLIGHT
Dos Equis Good Mexico Regional 4.22 0.70 145 14 4.5 NONLIGHT
Hamms Fair USA Regional 2.59 0.43 136 19 4.4 NONLIGHT
Heilmans Old Style Fair USA Regional 2.59 0.43 144 24 4.9 NONLIGHT
Heineken VeryGood Holland National 4.59 0.77 152 11 5.0 NONLIGHT
Henry Weinhard VeryGood USA Regional 3.65 0.61 149 7 4.7 NONLIGHT
Kirin Good Japan Regional 4.75 0.79 149 6 5.0 NONLIGHT
Kronenbourg VeryGood France Regional 4.39 0.73 170 7 5.2 NONLIGHT
Labatts VeryGood Canada Regional 3.15 0.53 147 17 5.0 NONLIGHT
Lowenbrau VeryGood USA National 2.89 0.48 157 15 4.9 NONLIGHT
Michelob VeryGood USA National 2.99 0.50 162 10 5.0 NONLIGHT
Miller High Life VeryGood USA National 2.49 0.42 149 17 4.7 NONLIGHT
Molson VeryGood Canada Regional 3.35 0.56 154 17 5.1 NONLIGHT
Old Milwaukee Good USA Regional 1.69 0.28 145 23 4.6 NONLIGHT
Olympia Good USA Regional 2.65 0.44 153 27 4.6 NONLIGHT
Pabst Blue Ribbon Good USA National 2.29 0.38 152 8 4.9 NONLIGHT
Rolling Rock Fair USA Regional 2.15 0.36 144 8 4.7 NONLIGHT
Schlitz VeryGood USA National 2.59 0.43 151 19 4.9 NONLIGHT
Schmidts Good USA Regional 1.79 0.30 147 7 4.7 NONLIGHT
Scotch Buy (Safeway) Fair USA Regional 1.59 0.27 145 18 4.5 NONLIGHT
St Pauli Girl Fair Germany Regional 4.59 0.77 144 21 4.7 NONLIGHT
Strohs Bohemian Style Good USA Regional 2.49 0.42 149 27 4.7 NONLIGHT
Tuborg Fair USA Regional 2.59 0.43 155 13 5.0 NONLIGHT
22

Questions for you

  • How many variables in the Beer dataset?
  • Which are metric?
  • Which are nominal?
  • Which are ordinal?
23

Discussion

  • Price is an example of a numerical variable.
  • Country of Origin is an example of a nominal variable:
    • You can not have more or less France-ness or Mexico-ness
  • Rating is an example of an ordinal variable:
    • A very good beer is better than a good beer but we do not know how much better.
24

Cross tab

  • A useful tool for exploring non-metric variables is the cross tab.
25

Cross tab

  • A useful tool for exploring non-metric variables is the cross tab.
  • Cross tabs that are small can be very useful in providing some indication of the relationships between categorical variables.
25

Cross tab

  • A useful tool for exploring non-metric variables is the cross tab.
  • Cross tabs that are small can be very useful in providing some indication of the relationships between categorical variables.
  • Since most Beers in our dataset are from the US, the following cross tab only looks at US beers against beers from all other countries combined.
25

Cross Tab: Rating v Origin

International v US

Int. US
VeryGood 4 7
Good 3 11
Fair 1 9

Is there a relationship between origin and rating?

26

Using all countries

USA Canada France Holland Mexico Germany Japan
VeryGood 7 2 1 1 0 0 0
Good 11 0 0 0 1 1 1
Fair 9 0 0 0 0 1 0

Is it as easy to find a relationship now?

27

Correspondence Analysis

  • Large cross tabulations can be summarised and visualised with a technique known as Correspondence Analysis.
28

Correspondence Analysis

  • Large cross tabulations can be summarised and visualised with a technique known as Correspondence Analysis.
  • This technique is mostly used to visualise the relationship between two variables.
28

Correspondence Analysis

  • Large cross tabulations can be summarised and visualised with a technique known as Correspondence Analysis.
  • This technique is mostly used to visualise the relationship between two variables.
  • The problem is considered high-dimensional since the number of categories rather than the number of variables is large.
28

Correspondence Analysis

  • Large cross tabulations can be summarised and visualised with a technique known as Correspondence Analysis.
  • This technique is mostly used to visualise the relationship between two variables.
  • The problem is considered high-dimensional since the number of categories rather than the number of variables is large.
  • On the next slide is the output from correspondence analysis
28

Correspondence Analysis

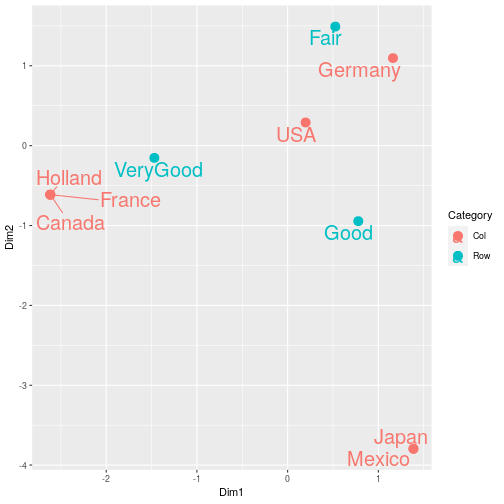
29

Other data

  • Data comes in even more unusual forms.
    • The list of your favourite musicians on Spotify
    • The words used in online reviews of hotels
    • A ranking of pairs of products from most similar to most dissimilar
30

Other data

  • Data comes in even more unusual forms.
    • The list of your favourite musicians on Spotify
    • The words used in online reviews of hotels
    • A ranking of pairs of products from most similar to most dissimilar
  • All of these types of data can be analysed using methods covered in the unit.
30

A Data Story

2
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow