Distance
High Dimensional Data Analysis
Anastasios Panagiotelis & Ruben Loaiza-Maya
Lecture 3
1
Why distance?
2
Why distance?
- Many problems that involve thinking about how similar or dissimilar two observations are. For example:
3
Why distance?
- Many problems that involve thinking about how similar or dissimilar two observations are. For example:
- May use the same marketing strategy for similar demographic groups.
- May lend money to applicants who are similar to those who pay debts back.
3
Why distance?
- Many problems that involve thinking about how similar or dissimilar two observations are. For example:
- May use the same marketing strategy for similar demographic groups.
- May lend money to applicants who are similar to those who pay debts back.
- Arguably the most important concept in data analysis is distance
3
Simple example
- Consider 3 individuals:
4
Simple example
- Consider 3 individuals:
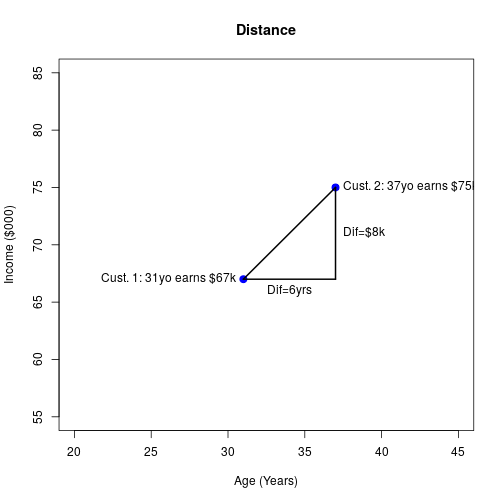
- Mr Orange: 37 years of age earns $75k a year
- Mr Red: 31 years of age earns $67k a year
- Mr Blue: 30 years of age earns $68k a year
4
Simple example
- Consider 3 individuals:
- Mr Orange: 37 years of age earns $75k a year
- Mr Red: 31 years of age earns $67k a year
- Mr Blue: 30 years of age earns $68k a year
- Which two are the most similar?
4
On a scatterplot
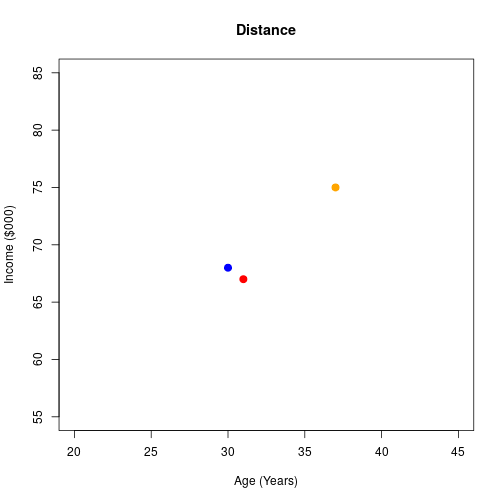
5
Distance as a number
- It is easy to think about three individuals but what if there are thousands of individuals?
6
Distance as a number
- It is easy to think about three individuals but what if there are thousands of individuals?
- In this case it will be useful to attach some number to the distance between pairs of individuals
6
Distance as a number
- It is easy to think about three individuals but what if there are thousands of individuals?
- In this case it will be useful to attach some number to the distance between pairs of individuals
- We will do it with a simple application of Pythagoras' theorem.
6
Finding the Distance
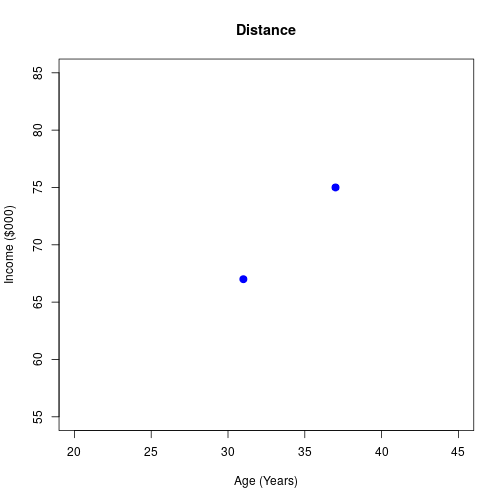
7
Finding the Distance
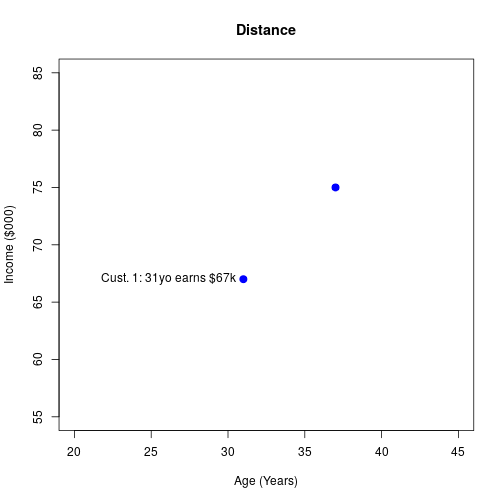
8
Finding the Distance
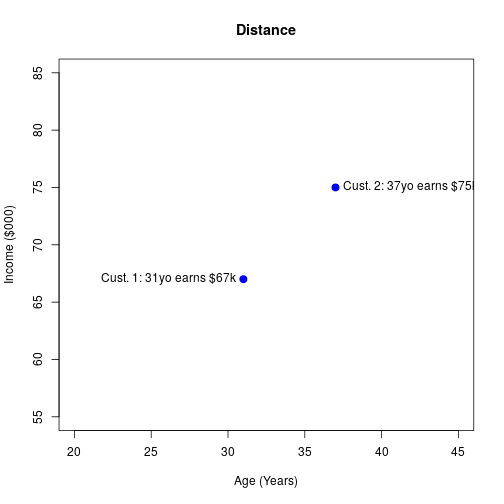
9
Finding the Distance
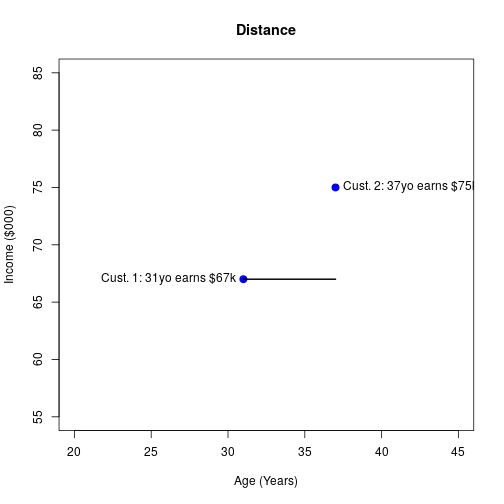
10
Finding the Distance
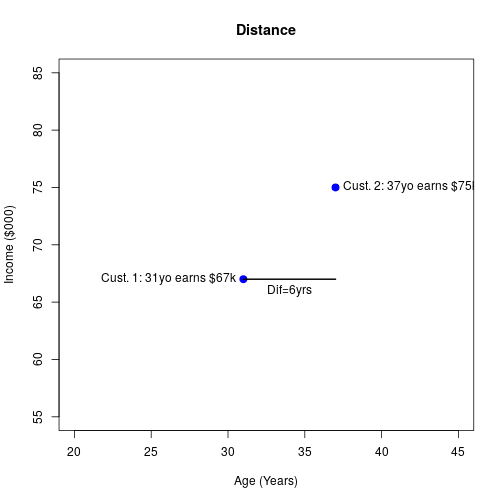
11
Finding the Distance
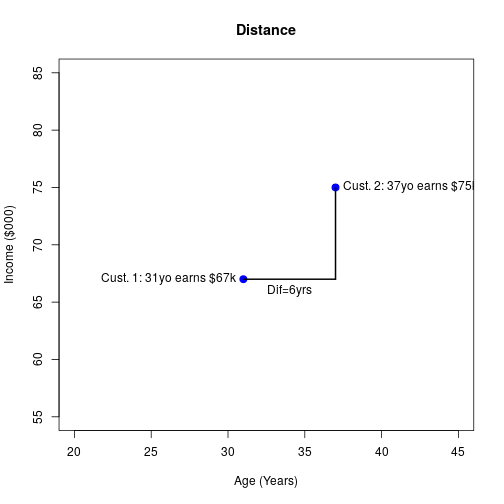
12
Finding the Distance
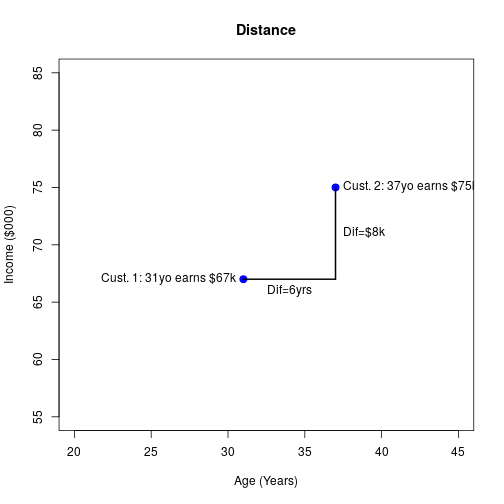
13
Finding the Distance
14
Finding the Distance
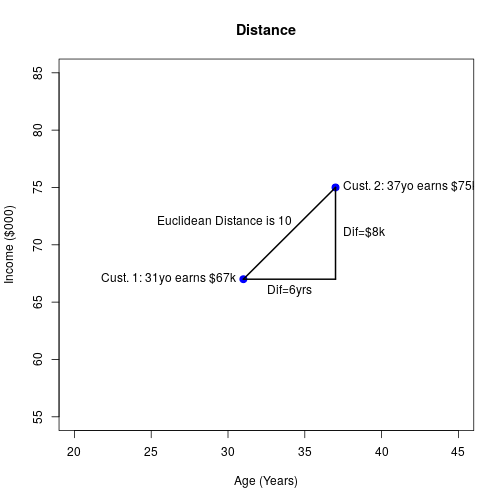
15
Euclidean distance
- In general there are more than two variables.
16
Euclidean distance
- In general there are more than two variables.
- Is there a way to apply our intuition in 2 dimensions to higher dimensions?
16
Euclidean distance
- In general there are more than two variables.
- Is there a way to apply our intuition in 2 dimensions to higher dimensions?
- Pythagoras' theorem can be generalised to higher dimensions.
16
Euclidean distance
- In general there are more than two variables.
- Is there a way to apply our intuition in 2 dimensions to higher dimensions?
- Pythagoras' theorem can be generalised to higher dimensions.
- This results in a concept of distance called Euclidean distance.
16
Euclidean distance
We measure p variables for two observations: xj is the measurement of variable j for observation x, yj is the measurement of variable j for observation y. Euclidean distance between x and y is:
D(x,y)= ⎷p∑j=1(xj−yj)2
17
Vectors
- Notice that x and y are examples of vectors.
18
Vectors
- Notice that x and y are examples of vectors.
- For example x=(x1x2) where x1 is age and x2 is income.
18
Vectors
- Notice that x and y are examples of vectors.
- For example x=(x1x2) where x1 is age and x2 is income.
- We can think of a data point as
18
Vectors
- Notice that x and y are examples of vectors.
- For example x=(x1x2) where x1 is age and x2 is income.
- We can think of a data point as
- A vector of attributes or measurements
18
Vectors
- Notice that x and y are examples of vectors.
- For example x=(x1x2) where x1 is age and x2 is income.
- We can think of a data point as
- A vector of attributes or measurements
- A point in space
18
Vectors
- Notice that x and y are examples of vectors.
- For example x=(x1x2) where x1 is age and x2 is income.
- We can think of a data point as
- A vector of attributes or measurements
- A point in space
- These are the same thing.
18
Other kinds of distance
- We will nearly always use Euclidean Distance in this unit, however there are other ways of understanding distance
- One example is the Manhattan Distance also known as block distance.
D(x,y)=p∑j=1∣∣xj−yj∣∣
19
Manhattan Distance
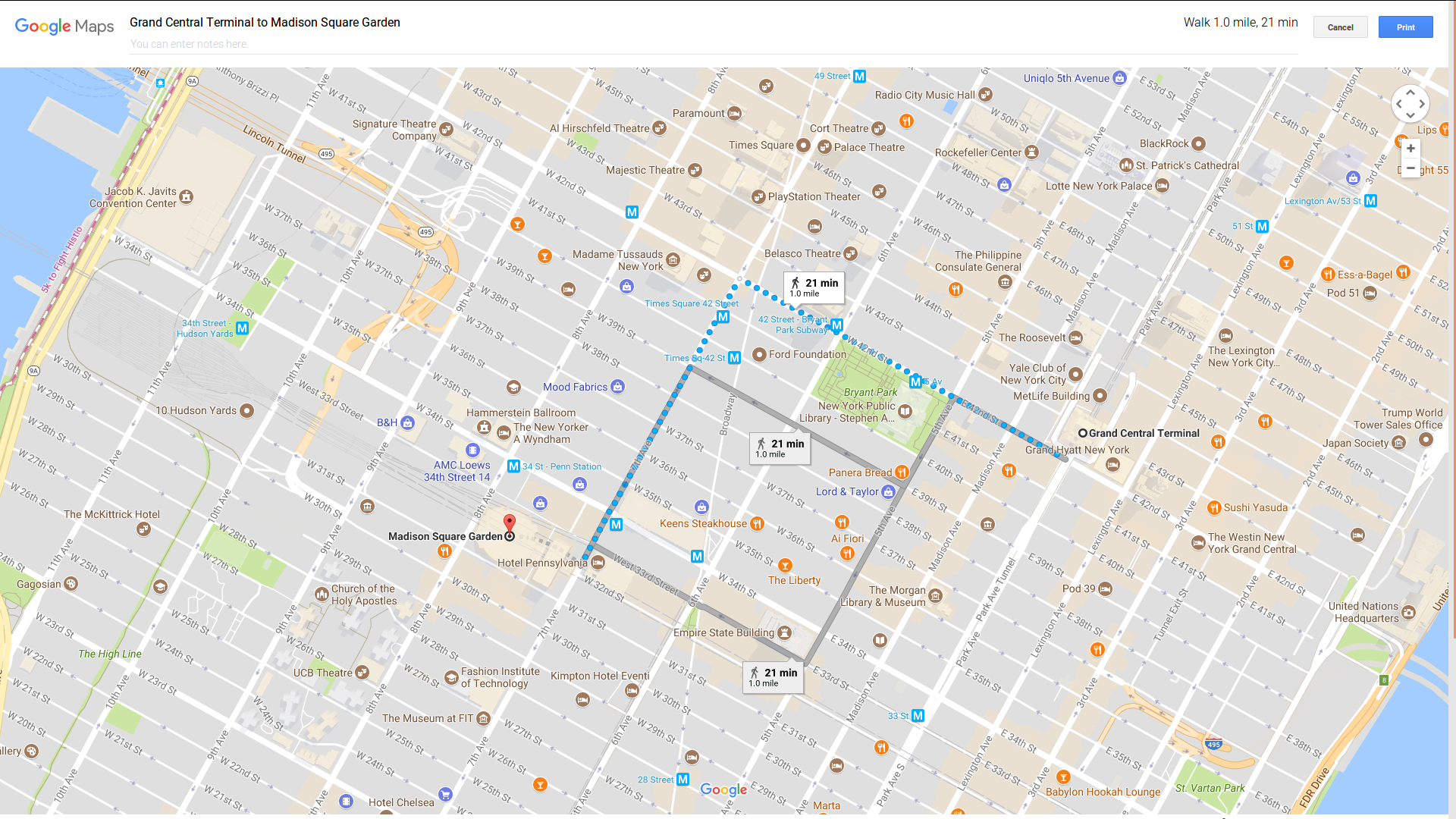
20
Distance and Standardising data
- We must be careful about the units of measurement.
21
Distance and Standardising data
- We must be careful about the units of measurement.
- Euclidean (and Manhattan) distance change for variables measured in different units.
21
Distance and Standardising data
- We must be careful about the units of measurement.
- Euclidean (and Manhattan) distance change for variables measured in different units.
- For this reason, it is common to calculate distance after the standardising data.
21
Distance and Standardising data
- We must be careful about the units of measurement.
- Euclidean (and Manhattan) distance change for variables measured in different units.
- For this reason, it is common to calculate distance after the standardising data.
- If the variables are all measured in the same units, then this standardisation is unecessary.
21
Distance and Standardising data
- We must be careful about the units of measurement.
- Euclidean (and Manhattan) distance change for variables measured in different units.
- For this reason, it is common to calculate distance after the standardising data.
- If the variables are all measured in the same units, then this standardisation is unecessary.
- Some distances are not sensitive to units of measurement (e.g. Mahalanobis Distance)
21
Distance in R
- R has its own special object for distances known as a
distobject
22
Distance in R
- R has its own special object for distances known as a
distobject - It can be obtained using the
dist()function
22
Distance in R
- R has its own special object for distances known as a
distobject - It can be obtained using the
dist()function - We are going to find Euclidean distances between the beers in the beers dataset. Use:
22
Distance in R
- R has its own special object for distances known as a
distobject - It can be obtained using the
dist()function - We are going to find Euclidean distances between the beers in the beers dataset. Use:
- Only beers with price greater than $4.50
- Only numeric variables.
- Standardised data
- Use the function
distto get the distances.
22
Load packages and data
library(dplyr)Beer<-readRDS('Beer.rds')23
Find Distances
Beer%>%filter(price>4.5)%>% #Only expensive Beers select_if(is.numeric)%>% #Only numeric variables scale%>% dist->d| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 0.0000 | 3.4298 | 3.8333 | 4.1632 | 4.1950 |
| 3.4298 | 0.0000 | 2.3009 | 2.8076 | 1.6260 |
| 3.8333 | 2.3009 | 0.0000 | 1.1482 | 3.2339 |
| 4.1632 | 2.8076 | 1.1482 | 0.0000 | 3.3188 |
| 4.1950 | 1.6260 | 3.2339 | 3.3188 | 0.0000 |
24
Labels
- Only numeric variables were used to compute distances.
- The names of the beers are not attached to the
distobject. - This can be achived by assigning the beer names to
attributes(d)$Labels - Here
dis thedistobject.
25
Use Beer Names
Beer%>%filter(price>4.5)%>% #Only expensive Beers pull(beer)-> #Get beer names attributes(d)$Labels #"Attach" them to dist object| Anchor Steam | Becks | Heineken | Kirin | St Pauli Girl | |
|---|---|---|---|---|---|
| Anchor Steam | 0.0000 | 3.4298 | 3.8333 | 4.1632 | 4.1950 |
| Becks | 3.4298 | 0.0000 | 2.3009 | 2.8076 | 1.6260 |
| Heineken | 3.8333 | 2.3009 | 0.0000 | 1.1482 | 3.2339 |
| Kirin | 4.1632 | 2.8076 | 1.1482 | 0.0000 | 3.3188 |
| St Pauli Girl | 4.1950 | 1.6260 | 3.2339 | 3.3188 | 0.0000 |
26
Your Turn
- Compute the distance without standardising the data.
27
Your Turn
- Compute the distance without standardising the data.
- Compute the Manhattan distance for standardised data.
27
Your Turn
- Compute the distance without standardising the data.
- Compute the Manhattan distance for standardised data.
- Compute the Manhattan distance for unstandardised data.
27
Non-Metric
28
Non-metric Data
- Can we define distance when the variables are non metric?
29
Non-metric Data
- Can we define distance when the variables are non metric?
- The answer is yes!
29
Non-metric Data
- Can we define distance when the variables are non metric?
- The answer is yes!
- We will discuss two approaches:
29
Non-metric Data
- Can we define distance when the variables are non metric?
- The answer is yes!
- We will discuss two approaches:
- Jaccard Similarity/ Distance
- Dummy Variables
29
First a motivation
- Many people use music streaming services like Spotify.
30
First a motivation
- Many people use music streaming services like Spotify.
- One of the attractions of these services is they they recommend artists based on the favourite artists of other users who have similar taste in music.
30
First a motivation
- Many people use music streaming services like Spotify.
- One of the attractions of these services is they they recommend artists based on the favourite artists of other users who have similar taste in music.
- The data in this case is in the form of a list of favourite artists.
30
Distance in musical taste
- Suppose there are three customers with the following favourite artists
31
Distance in musical taste
- Suppose there are three customers with the following favourite artists
- Customer A: Post Malone, Drake, Lil Peep, Billie Eilish
- Customer B: Post Malone, Lil Peep, Juice Wrld
- Customer C: Billie Eilish, Ed Sheeran, Ariana Grande
31
Distance in musical taste
- Suppose there are three customers with the following favourite artists
- Customer A: Post Malone, Drake, Lil Peep, Billie Eilish
- Customer B: Post Malone, Lil Peep, Juice Wrld
- Customer C: Billie Eilish, Ed Sheeran, Ariana Grande
- How do we measure which customers have similar taste and which have different taste?
31
Jaccard Similarity and Distance
- Jaccard similarity gives us a measure of how close two sets are, in this case the set of each customers favourite musician. The formula is J(A,B)=|A∩B||A∪B|
- Where |A∩B| is the number of elements in both set A and set B and |A∪B| is the number of elements in either set A or set B.
32
Jaccard Similarity
- In our example
33
Jaccard Similarity
- In our example
- A∩B={Post Malone, Lil Peep}
- |A∩B|=2
- A∪B={Post Malone, Lil Peep,Drake, Billie Eilish, Juice Wrld}
- |A∪B|=5
33
Jaccard Similarity
- In our example
- A∩B={Post Malone, Lil Peep}
- |A∩B|=2
- A∪B={Post Malone, Lil Peep,Drake, Billie Eilish, Juice Wrld}
- |A∪B|=5
- The Jaccard similarity will be J=2/5=0.4. The Jaccard distance is dJ=1−J=1−0.4=0.6
33
Using dummy variables
- Alternatively the same data can be coded using dummy variables:
34
Using dummy variables
- Alternatively the same data can be coded using dummy variables:
- Xj=1 if artist j is a favourite of customer x
- Xj=0 otherwise
34
Using dummy variables
- Alternatively the same data can be coded using dummy variables:
- Xj=1 if artist j is a favourite of customer x
- Xj=0 otherwise
- The usual distance measures such as Euclidean or Manhattan distance can then be used.
34
Collaborative Filtering
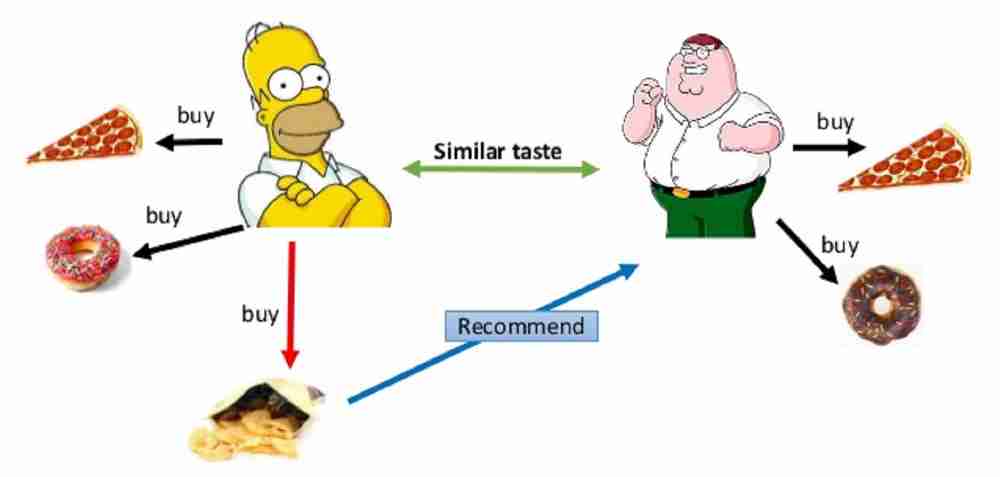
Figure by Mohamed Ben Ellefi
35
Recommender Systems
- Famous recommender systems are used by Amazon, Netflix, Alibaba amongst others.
- These systems are usually a hybrid of
- Collaborative Filtering
- Content-based Filtering
- The method we discussed is more specifically called memory-based collaborative filtering.
36
Axioms of Distance
- Care should be taken when using the word distance.
- In formal mathematics a distance is a function with two inputs that has to satisfy four properties.
- These four properties are called axioms.
- The distance measures that we have discussed satisfy the axioms
37
Axioms of Distance
- Non-negative: d(x,y)≥0
- There cannot be negative distance.
- Symmetry: d(x,y)=d(y,x)
- It cannot be a different distance from Melbourne to Brisbane that from Brisbane to Melbourne.
38
Axioms of Distance
- Identity of indiscernables: if d(x,y)=0 then x=y and vice versa
- The distance from Melbourne to some place is zero then that place is Melbourne. Similarly the distance from Melbourne to itself is zero.
- Triangle inequality: d(x,z)≤d(x,y)+d(y,z) It cannot be closer to go from Melbourne to Brisbane via Sydney than it is to go from Melbourne to Brisbane directly.
39
Conclusions
- That concludes the topic on distance.
40
Conclusions
- That concludes the topic on distance.
- This is relevant to the following topics
40
Conclusions
- That concludes the topic on distance.
- This is relevant to the following topics
- Cluster Analysis
40
Conclusions
- That concludes the topic on distance.
- This is relevant to the following topics
- Cluster Analysis
- Multidimensional Scaling (MDS)
40
Conclusions
- That concludes the topic on distance.
- This is relevant to the following topics
- Cluster Analysis
- Multidimensional Scaling (MDS)
- Now an exercise
40
Distances between tweets
- Find someone on Twitter or a similar social media site
- Find the first two tweets
- Think of a way to compute a Jaccard distance between their tweets
- Hint: Think of the words used in the tweet as a set
41