Cluster Analysis
High Dimensional Data Analysis
Anastasios Panagiotelis & Ruben Loaiza-Maya
Lecture 4
Why Clustering?
Market Segmentation
- A common strategy in marketing is to analyse different segments of the market.
Market Segmentation
- A common strategy in marketing is to analyse different segments of the market.
- Sometimes the purpose is to segment based on a single variable:
Market Segmentation
- A common strategy in marketing is to analyse different segments of the market.
- Sometimes the purpose is to segment based on a single variable:
- Gender
Market Segmentation
- A common strategy in marketing is to analyse different segments of the market.
- Sometimes the purpose is to segment based on a single variable:
- Gender
- Age
Market Segmentation
- A common strategy in marketing is to analyse different segments of the market.
- Sometimes the purpose is to segment based on a single variable:
- Gender
- Age
- Income
Market Segmentation
- A common strategy in marketing is to analyse different segments of the market.
- Sometimes the purpose is to segment based on a single variable:
- Gender
- Age
- Income
- An alternative is to segment using all available information
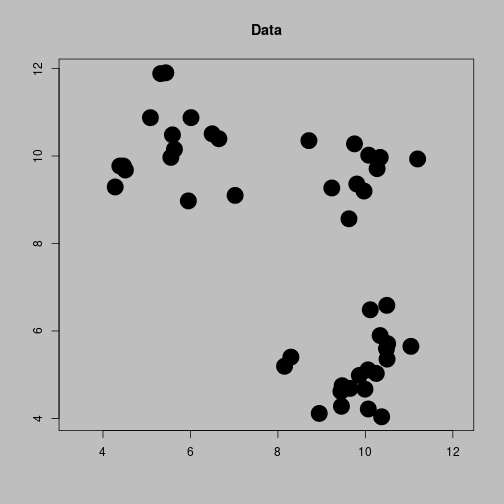
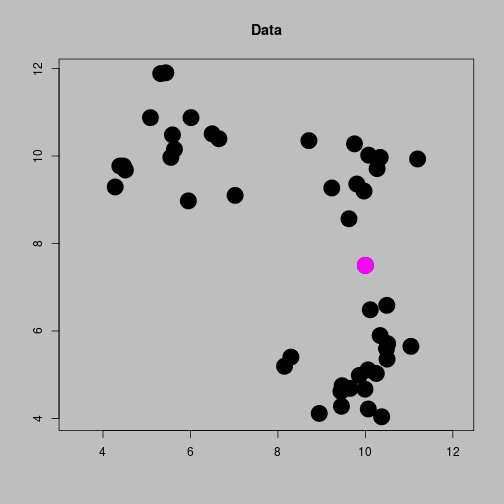
A 2-dimensional example
- Consider that data is collected for customers’ age and income.
A 2-dimensional example
- Consider that data is collected for customers’ age and income.
- These can be plotted on a scatterplot to see if any obvious segments or clusters are present.
A 2-dimensional example
- Consider that data is collected for customers’ age and income.
- These can be plotted on a scatterplot to see if any obvious segments or clusters are present.
- The following data are not real data but are simulated
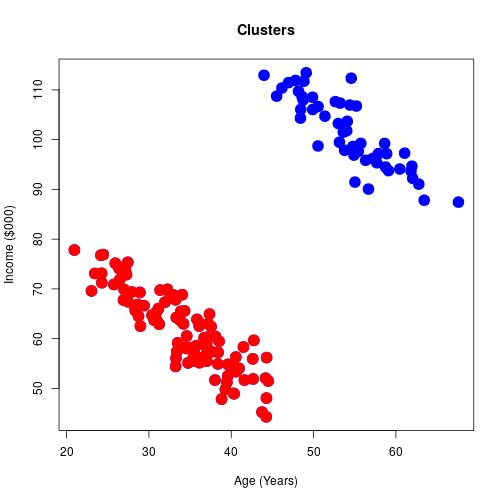
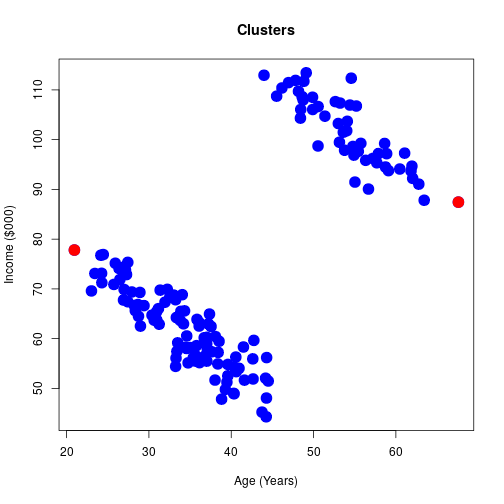
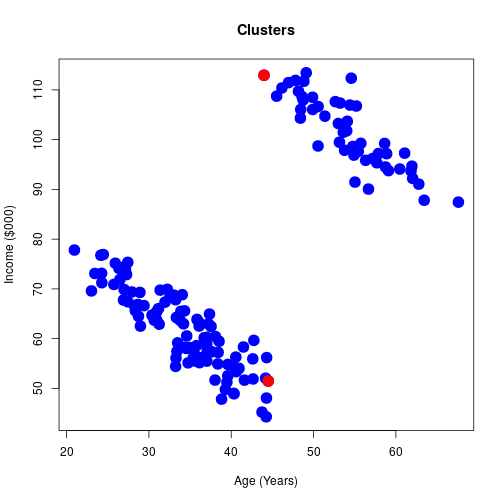
Age v Income
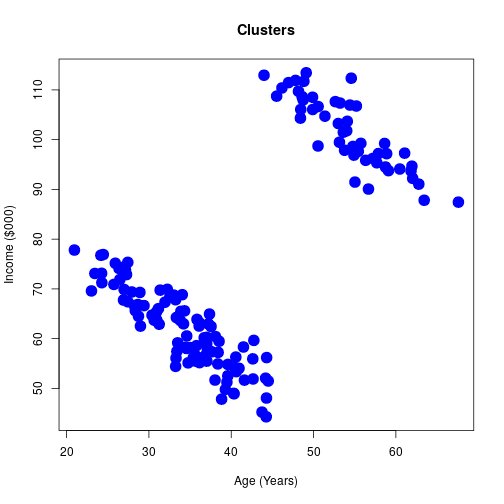
Obvious clusters
Only income
Only age
Summary
- Using just one variable can be misleading.
Summary
- Using just one variable can be misleading.
- When there are more than 2 variables just looking at a scatterplot doesn’t work.
Summary
- Using just one variable can be misleading.
- When there are more than 2 variables just looking at a scatterplot doesn’t work.
- Instead algorithms can be used to find the clusters in a sensible way, even in high dimensions.
Real Example 1
- The dataset mtcars is an R dataset that originally came from a 1974 magazine called Motor Trends
Real Example 1
- The dataset mtcars is an R dataset that originally came from a 1974 magazine called Motor Trends
- There are 32 cars which are measured on 11 variables such as miles per gallon, number of cylinders, horsepower and weight.
Real Example 1
- The dataset mtcars is an R dataset that originally came from a 1974 magazine called Motor Trends
- There are 32 cars which are measured on 11 variables such as miles per gallon, number of cylinders, horsepower and weight.
- It can be loaded into the workspace using the command
data(mtcars)
MT Cars data
| MakeModel | mpg | cyl | disp | hp | drat | wt | qsec | vs | am | gear | carb |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mazda RX4 | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.620 | 16.46 | 0 | 1 | 4 | 4 |
| Mazda RX4 Wag | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.875 | 17.02 | 0 | 1 | 4 | 4 |
| Datsun 710 | 22.8 | 4 | 108.0 | 93 | 3.85 | 2.320 | 18.61 | 1 | 1 | 4 | 1 |
| Hornet 4 Drive | 21.4 | 6 | 258.0 | 110 | 3.08 | 3.215 | 19.44 | 1 | 0 | 3 | 1 |
| Hornet Sportabout | 18.7 | 8 | 360.0 | 175 | 3.15 | 3.440 | 17.02 | 0 | 0 | 3 | 2 |
| Valiant | 18.1 | 6 | 225.0 | 105 | 2.76 | 3.460 | 20.22 | 1 | 0 | 3 | 1 |
| Duster 360 | 14.3 | 8 | 360.0 | 245 | 3.21 | 3.570 | 15.84 | 0 | 0 | 3 | 4 |
| Merc 240D | 24.4 | 4 | 146.7 | 62 | 3.69 | 3.190 | 20.00 | 1 | 0 | 4 | 2 |
| Merc 230 | 22.8 | 4 | 140.8 | 95 | 3.92 | 3.150 | 22.90 | 1 | 0 | 4 | 2 |
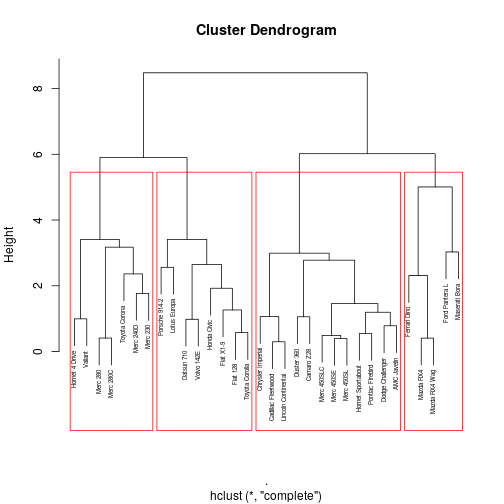
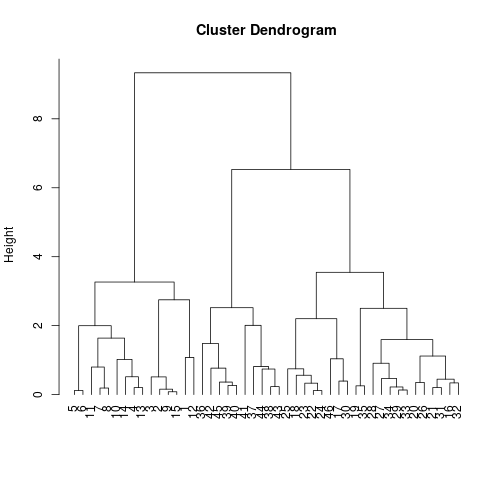
Dendrogram
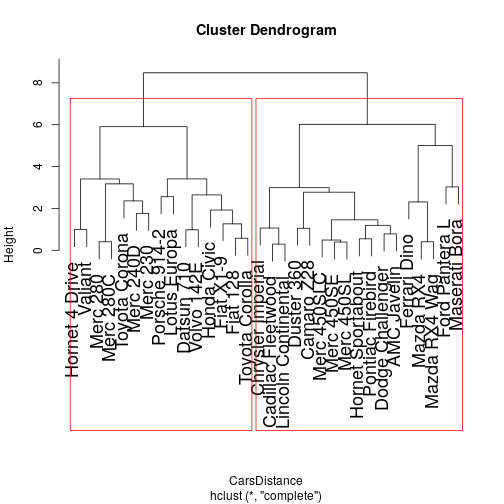
Real Example 2
- A business to business example with 440 customers of a wholesaler
Real Example 2
- A business to business example with 440 customers of a wholesaler
- The variables are annual spend in the following 6 categories:
Real Example 2
- A business to business example with 440 customers of a wholesaler
- The variables are annual spend in the following 6 categories:
- Fresh food
- Milk
- Groceries
- Frozen
- Detergents/Paper
- Delicatessen
Real Example 2
- A business to business example with 440 customers of a wholesaler
- The variables are annual spend in the following 6 categories:
- Fresh food
- Milk
- Groceries
- Frozen
- Detergents/Paper
- Delicatessen
- These data are available on Moodle.
Cluster centroids
After clustering we get the following cluster means.
| Cluster | Fresh | Milk | Grocery | Frozen | Detergents_Paper | Delicassen |
|---|---|---|---|---|---|---|
| 1 | 35941 | 6044 | 6289 | 6714 | 1040 | 3049 |
| 2 | 8253 | 3825 | 5280 | 2573 | 1773 | 1137 |
| 3 | 8000 | 18511 | 27574 | 1997 | 12407 | 2252 |
Approaches to Clustering
- Hierarchical: Path of solutions:
Approaches to Clustering
- Hierarchical: Path of solutions:
- Agglomerative: At start every observation is a cluster. Merge the most similar clusters step by step until all observations in one cluster.
Approaches to Clustering
- Hierarchical: Path of solutions:
- Agglomerative: At start every observation is a cluster. Merge the most similar clusters step by step until all observations in one cluster.
- Divisive: At start all observations in one cluster. Split step by step until each observation is in its own cluster.
Approaches to Clustering
- Hierarchical: Path of solutions:
- Agglomerative: At start every observation is a cluster. Merge the most similar clusters step by step until all observations in one cluster.
- Divisive: At start all observations in one cluster. Split step by step until each observation is in its own cluster.
- Non-hierarchical: Choose the number of clusters ex ante. No merging or splitting.
Our focus
- Our main focus will be on agglomerative hierarchical methods.
Our focus
- Our main focus will be on agglomerative hierarchical methods.
- Divisive hierarchical methods are very slow and we do not cover them at all.
Our focus
- Our main focus will be on agglomerative hierarchical methods.
- Divisive hierarchical methods are very slow and we do not cover them at all.
- We consider one example of a non-hierarchical method known as the k-means algorithm.
Definition of Clustering
- Oxford Dictionary: A group of similar things or people positioned or occurring closely together
Definition of Clustering
- Oxford Dictionary: A group of similar things or people positioned or occurring closely together
- Collins Dictionary: A number of things growing, fastened, or occurring close together
Definition of Clustering
- Oxford Dictionary: A group of similar things or people positioned or occurring closely together
- Collins Dictionary: A number of things growing, fastened, or occurring close together
- Note the importance of closeness or distance. We need two concepts of distance
Definition of Clustering
- Oxford Dictionary: A group of similar things or people positioned or occurring closely together
- Collins Dictionary: A number of things growing, fastened, or occurring close together
- Note the importance of closeness or distance. We need two concepts of distance
- Distance between observations.
- Distance between clusters.
A distance between clusters
- Let A be a cluster with observations {a1,a2,…,aI} and B be a cluster with points {b1,b2,…,bJ}.
A distance between clusters
- Let A be a cluster with observations {a1,a2,…,aI} and B be a cluster with points {b1,b2,…,bJ}.
- The calligraphic script A or B denotes a cluster with possibly more than one point.
A distance between clusters
- Let A be a cluster with observations {a1,a2,…,aI} and B be a cluster with points {b1,b2,…,bJ}.
- The calligraphic script A or B denotes a cluster with possibly more than one point.
- The bold scipt ai or bj denotes a vector of attributes (e.g. age and income) for each observation.
A distance between clusters
- Let A be a cluster with observations {a1,a2,…,aI} and B be a cluster with points {b1,b2,…,bJ}.
- The calligraphic script A or B denotes a cluster with possibly more than one point.
- The bold scipt ai or bj denotes a vector of attributes (e.g. age and income) for each observation.
- Rather than vectors, it is much easier to think of each observation as a point in a scatterplot.
Single Linkage
One way of defining the distance between clusters A and B is
D(A,B)=mini,jD(ai,bj)
This is called single linkage or nearest neighbour.
Single Linkage
Single Linkage
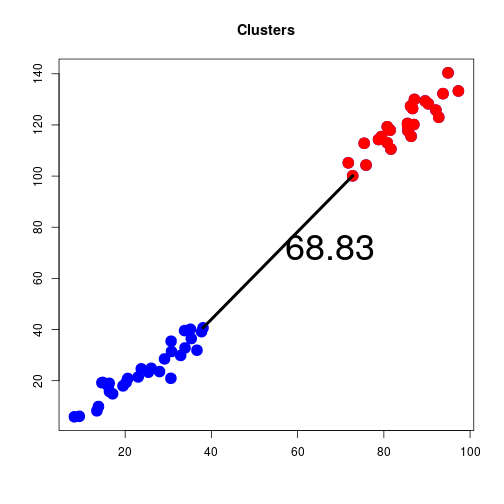
Complete Linkage
Another way of defining the distance between A and B is
D(A,B)=maxi,jD(ai,bj)
This is called complete linkage or furthest neighbour.
Complete Linkage
Complete Linkage
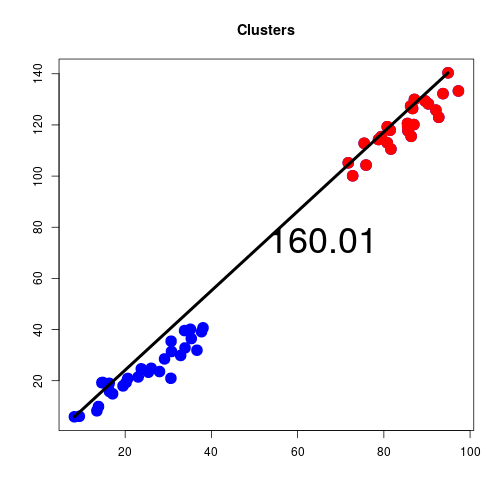
Complete linkage
- In the previous example all points in the red cluster are within a distance of 160.01 of all points in the blue cluster.
- This is why it is called complete linkage.
A simple example
- Over the next couple of slides we will go through the entire process of agglomerative clustering
A simple example
- Over the next couple of slides we will go through the entire process of agglomerative clustering
- We will use Euclidean distance to define distance between points
A simple example
- Over the next couple of slides we will go through the entire process of agglomerative clustering
- We will use Euclidean distance to define distance between points
- We will use single linkage to define the distance between clusters
A simple example
- Over the next couple of slides we will go through the entire process of agglomerative clustering
- We will use Euclidean distance to define distance between points
- We will use single linkage to define the distance between clusters
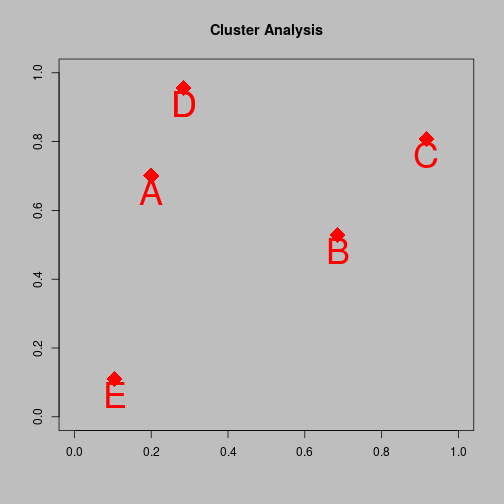
- There are only five observations and two variables
Agglomerative clustering
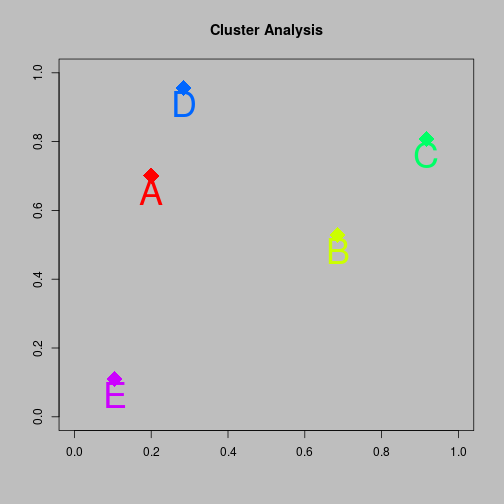
Agglomerative clustering
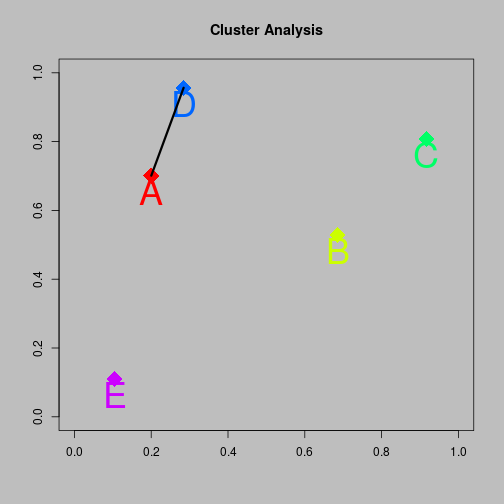
Agglomerative clustering
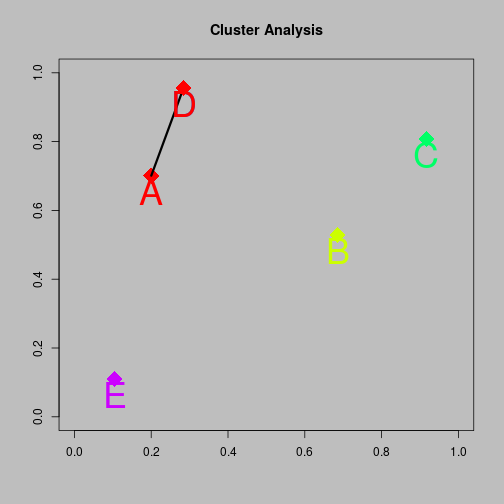
Agglomerative clustering
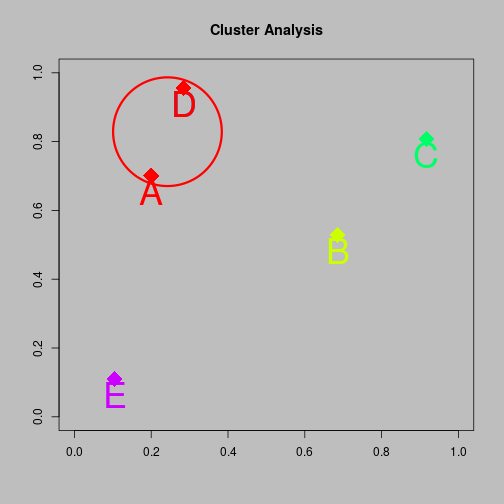
Agglomerative clustering
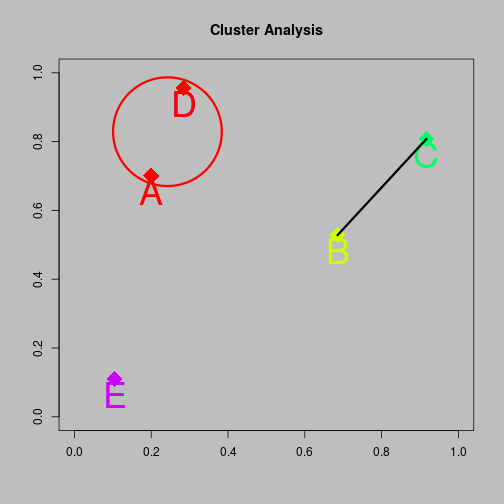
Agglomerative clustering
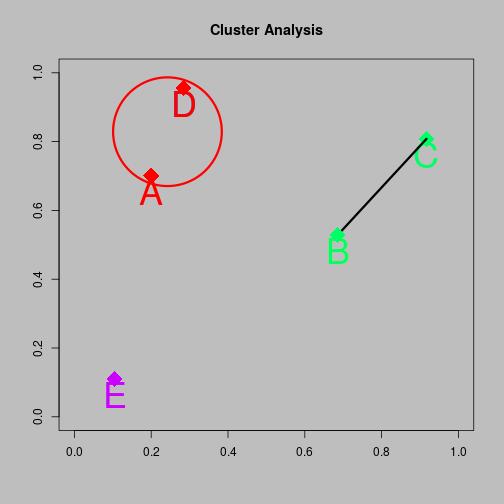
Agglomerative clustering
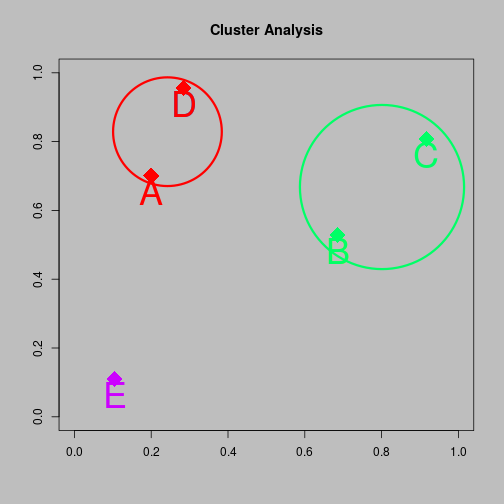
Agglomerative clustering
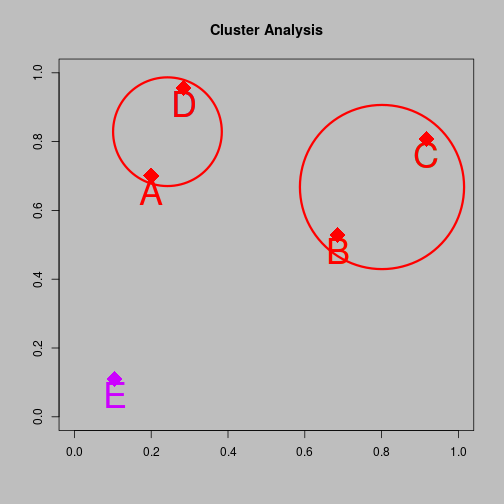
Agglomerative clustering
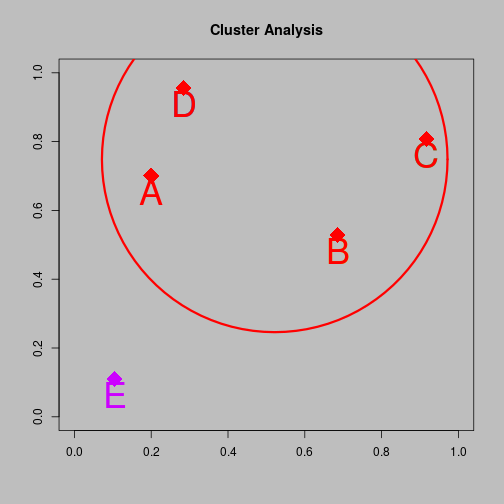
Agglomerative clustering
Hierarchical Clustering
- 5-cluster solution A and B and C and D and E
Hierarchical Clustering
- 5-cluster solution A and B and C and D and E
- 4-cluster solution {A,D} and B and C and E
Hierarchical Clustering
- 5-cluster solution A and B and C and D and E
- 4-cluster solution {A,D} and B and C and E
- 3-cluster solution {A,D} and {B, C} and E
Hierarchical Clustering
- 5-cluster solution A and B and C and D and E
- 4-cluster solution {A,D} and B and C and E
- 3-cluster solution {A,D} and {B, C} and E
- 2-cluster solution {A,B, C,D} and E
Hierarchical Clustering
- 5-cluster solution A and B and C and D and E
- 4-cluster solution {A,D} and B and C and E
- 3-cluster solution {A,D} and {B, C} and E
- 2-cluster solution {A,B, C,D} and E
- 1-cluster solution {A,B, C,D E}
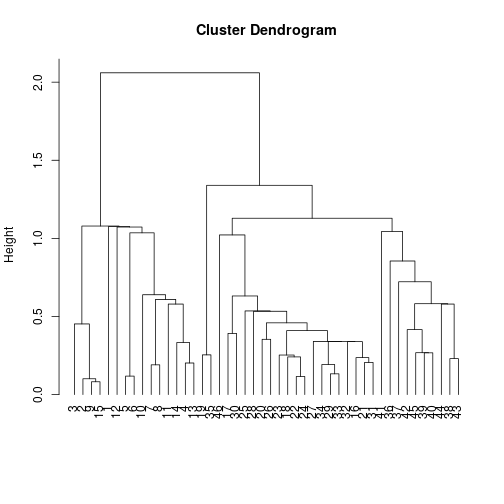
Dendrogram
- The Dendrogram is a useful tool for analysing a cluster solution.
Dendrogram
- The Dendrogram is a useful tool for analysing a cluster solution.
- Observations are on one axis (usually x)
Dendrogram
- The Dendrogram is a useful tool for analysing a cluster solution.
- Observations are on one axis (usually x)
- The distance between clusters is on other axis (usually y).
Dendrogram
- The Dendrogram is a useful tool for analysing a cluster solution.
- Observations are on one axis (usually x)
- The distance between clusters is on other axis (usually y).
- From the Dendrogram one can see the order in which the clusters are merged.
Dendrogram
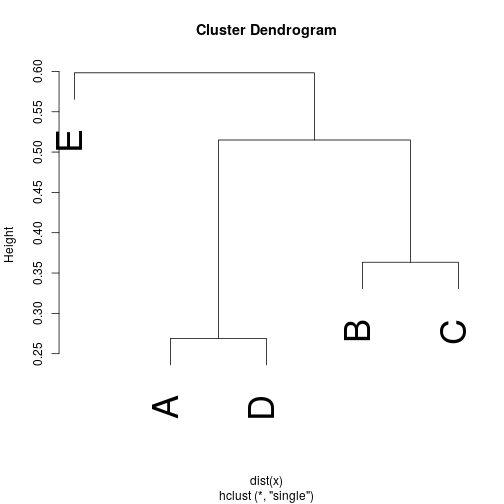
Interpretation of Dendrogram
- Think of the axis with distance (y-axis) as the measuring a 'tolerance level'
Interpretation of Dendrogram
- Think of the axis with distance (y-axis) as the measuring a 'tolerance level'
- If the distance between two clusters is within the tolerance they are merged into one cluster.
Interpretation of Dendrogram
- Think of the axis with distance (y-axis) as the measuring a 'tolerance level'
- If the distance between two clusters is within the tolerance they are merged into one cluster.
- As tolerance increases more and more clusters are merged leading to less clusters overall.
Clustering in R
- Clustering in R requires at most 3 steps
Clustering in R
- Clustering in R requires at most 3 steps
- Standardise the data if they are in different units (using the function
scale)
- Standardise the data if they are in different units (using the function
Clustering in R
- Clustering in R requires at most 3 steps
- Standardise the data if they are in different units (using the function
scale) - Find the distance between all pairs of observations (using the function
dist)
- Standardise the data if they are in different units (using the function
Clustering in R
- Clustering in R requires at most 3 steps
- Standardise the data if they are in different units (using the function
scale) - Find the distance between all pairs of observations (using the function
dist) - Cluster the data using the function
hclust
- Standardise the data if they are in different units (using the function
Clustering in R
- Clustering in R requires at most 3 steps
- Standardise the data if they are in different units (using the function
scale) - Find the distance between all pairs of observations (using the function
dist) - Cluster the data using the function
hclust
- Standardise the data if they are in different units (using the function
- Try this with the
mtcarsdataset. Use Euclidean distance and complete linkage. - Store the result of
hclustin a variable called CarsCluster.
Clustering in R
data(mtcars)mtcars%>% scale%>% dist%>% hclust(method="complete")-> CarsClusterDendrogram in R
plot(CarsCluster,cex=0.5)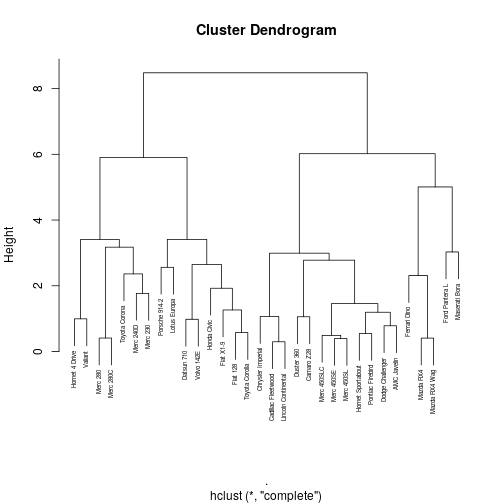
Identifying clusters
CarsCluster%>%plot(cex=0.5)CarsCluster%>%rect.hclust(k=2)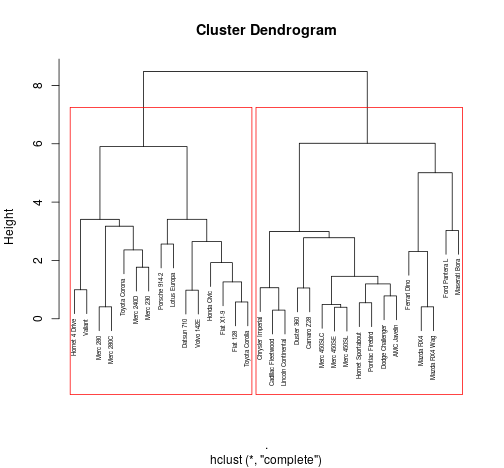
Dendrogram in R
For an interactive tool try:
identify(CarsCluster)Press the escape key when you are finished.
Choosing the number of clusters
Choosing clusters
- Although hierarchical clustering gives a solution for any number of clusters, ultimately we only want to focus on one of these solutions.
Choosing clusters
- Although hierarchical clustering gives a solution for any number of clusters, ultimately we only want to focus on one of these solutions.
- There is no correct number of clusters. Choosing the number of clusters depends on the context.
Choosing clusters
- Although hierarchical clustering gives a solution for any number of clusters, ultimately we only want to focus on one of these solutions.
- There is no correct number of clusters. Choosing the number of clusters depends on the context.
- There are however poor choices for the number of clusters.
Choosing clusters
- Do not choose too many clusters:
Choosing clusters
- Do not choose too many clusters:
- A firm developing a different marketing strategy for each market segment may not have the resources to develop a large number of unique strategies.
Choosing clusters
- Do not choose too many clusters:
- A firm developing a different marketing strategy for each market segment may not have the resources to develop a large number of unique strategies.
- Do not choose too few clusters:
Choosing clusters
- Do not choose too many clusters:
- A firm developing a different marketing strategy for each market segment may not have the resources to develop a large number of unique strategies.
- Do not choose too few clusters:
- If you choose the 1-cluster solution there is no point in doing clustering at all.
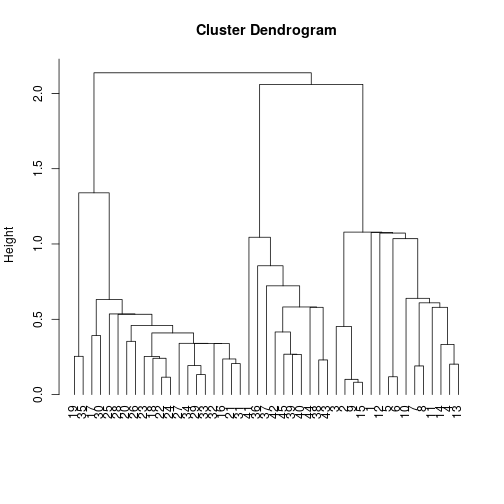
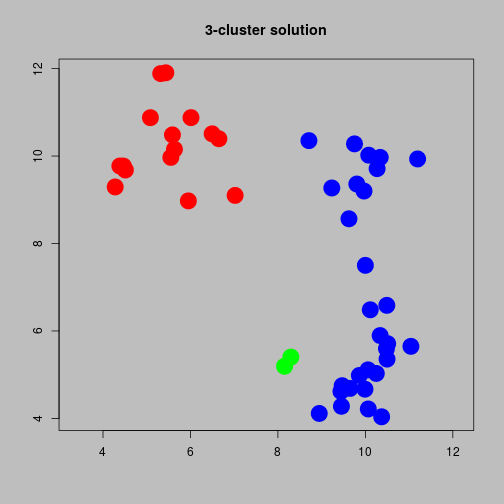
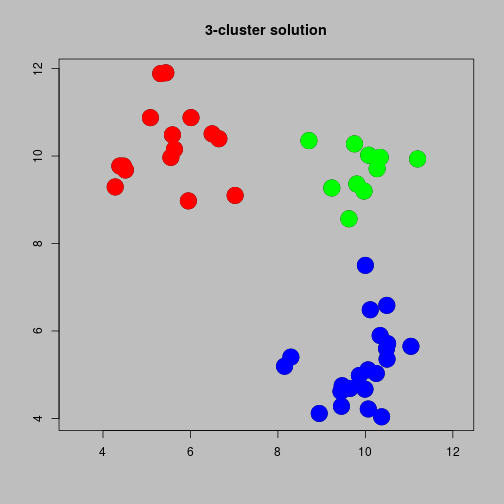
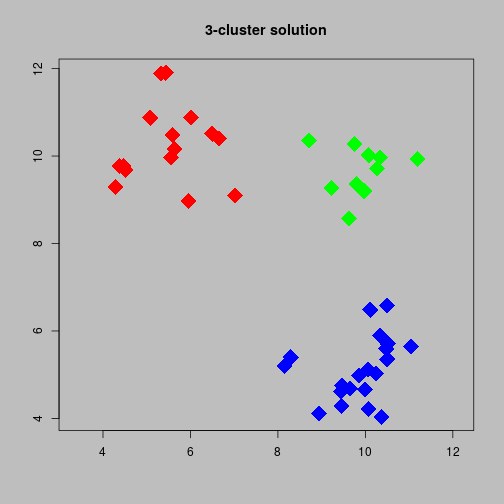
Using dendrogram
- One criterion is that the number of clusters is stable over a wide range of tolerance.
Using dendrogram
- One criterion is that the number of clusters is stable over a wide range of tolerance.
- The plot on the next slide shows a 3 cluster solution.
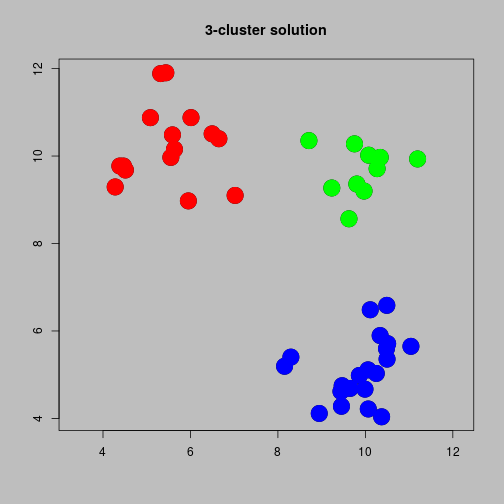
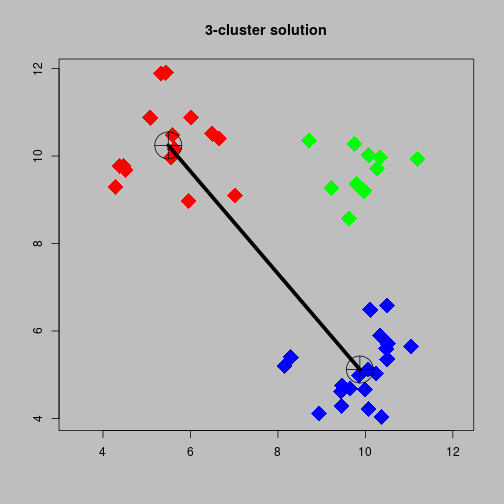
Three cluster solution
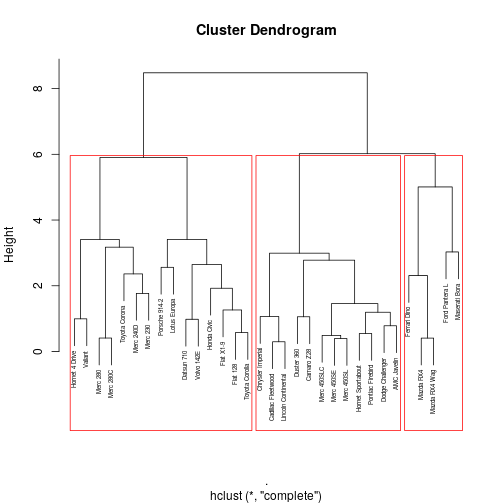
Stability
- The tolerance for a three cluster solution is about 5.9.
Stability
- The tolerance for a three cluster solution is about 5.9.
- If the tolerance is increased by a very small amount then we will have a two cluster solution.
Stability
- The tolerance for a three cluster solution is about 5.9.
- If the tolerance is increased by a very small amount then we will have a two cluster solution.
- If the tolerance is decreased by a very small amount then we will have a four cluster solution.
Two cluster solution
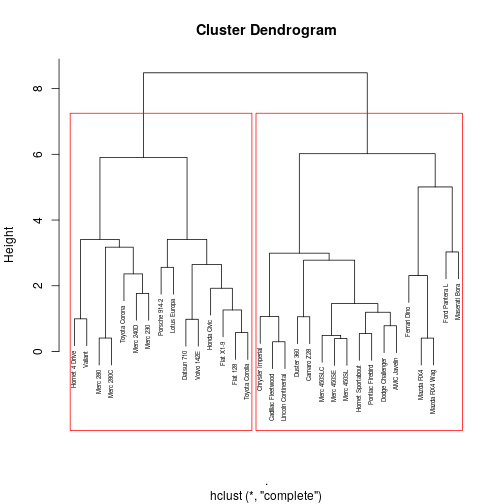
Four cluster solution
Stability
- In the previous example
Stability
- In the previous example
- The three cluster solution is not stable
Stability
- In the previous example
- The three cluster solution is not stable
- The two and four cluster solutions are stable
Stability
- In the previous example
- The three cluster solution is not stable
- The two and four cluster solutions are stable
- In general look for a long stretch of tolerance, over which the number of clusters does not change.
Extracting the clusters
For a given number of clusters we can create a new variable indicating cluster membership via the cutree function.
mem<-cutree(CarsCluster,2)| x | |
|---|---|
| Mazda RX4 | 1 |
| Mazda RX4 Wag | 1 |
| Datsun 710 | 2 |
| Hornet 4 Drive | 2 |
| Hornet Sportabout | 1 |
| Valiant | 2 |
| Duster 360 | 1 |
| Merc 240D | 2 |
| Merc 230 | 2 |
| Merc 280 | 2 |
| Merc 280C | 2 |
| Merc 450SE | 1 |
| Merc 450SL | 1 |
| Merc 450SLC | 1 |
| Cadillac Fleetwood | 1 |
| Lincoln Continental | 1 |
| Chrysler Imperial | 1 |
| Fiat 128 | 2 |
| Honda Civic | 2 |
| Toyota Corolla | 2 |
| Toyota Corona | 2 |
| Dodge Challenger | 1 |
| AMC Javelin | 1 |
| Camaro Z28 | 1 |
| Pontiac Firebird | 1 |
| Fiat X1-9 | 2 |
| Porsche 914-2 | 2 |
| Lotus Europa | 2 |
| Ford Pantera L | 1 |
| Ferrari Dino | 1 |
| Maserati Bora | 1 |
| Volvo 142E | 2 |
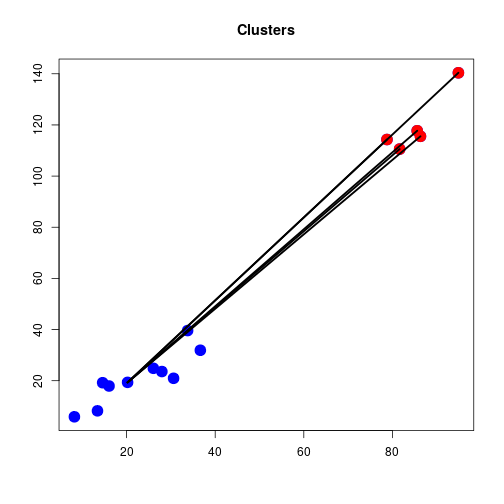
Pros and Cons of Single Linkage
- Pros:
- Single linkage is very easy to understand.
- Single linkage is a very fast algorithm.
Pros and Cons of Single Linkage
- Pros:
- Single linkage is very easy to understand.
- Single linkage is a very fast algorithm.
- Cons:
- Single linkage is very sensitive to single observations which leads to chaining.
- Complete linkage avoids this problem and gives more compact clusters with a similar diameter.
Chaining
Single Linkage Dendrogram
Single Linkage
Add one observation
New solution
Dendrogram with Chaining
Robustness
- In general adding a single observation should not dramatically change the analysis.
Robustness
- In general adding a single observation should not dramatically change the analysis.
- In this instance the new observation was not even an outlier.
Robustness
- In general adding a single observation should not dramatically change the analysis.
- In this instance the new observation was not even an outlier.
- A term used for such an observation is an inlier.
Robustness
- In general adding a single observation should not dramatically change the analysis.
- In this instance the new observation was not even an outlier.
- A term used for such an observation is an inlier.
- Methods that are not affected by single observations are often called robust.
Robustness
- In general adding a single observation should not dramatically change the analysis.
- In this instance the new observation was not even an outlier.
- A term used for such an observation is an inlier.
- Methods that are not affected by single observations are often called robust.
- Let's see if complete linkage is robust to the inlier.
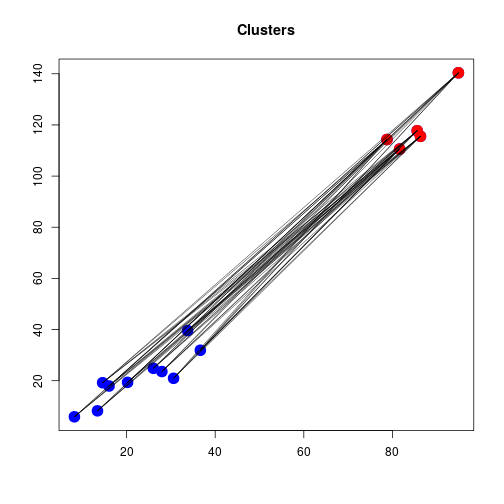
Complete Linkage
Complete Linkage: Dendrogram
Disadvantages of CL
- Complete Linkage overcomes chaining and is robust to inliers
Disadvantages of CL
- Complete Linkage overcomes chaining and is robust to inliers
- However, since the distance between clusters only depends on two observations it can still be sensitive to outliers.
Disadvantages of CL
- Complete Linkage overcomes chaining and is robust to inliers
- However, since the distance between clusters only depends on two observations it can still be sensitive to outliers.
- The following methods are more robust and should be preferred
Disadvantages of CL
- Complete Linkage overcomes chaining and is robust to inliers
- However, since the distance between clusters only depends on two observations it can still be sensitive to outliers.
- The following methods are more robust and should be preferred
- Average Linkage
- Centroid Method
- Ward’s Method
Average Linkage
The distance between two clusters can be defined so that it is based on all the pairwise distances between the elements of each cluster. D(A,B)=1|A||B||A|∑i=1|B|∑j=1D(ai,bj) Here |A| is the number of observations in cluster A and |B| is the number of observations in cluster B
Average Linkage
- Average linkage can be called different things
Average Linkage
- Average linkage can be called different things
- Between groups method.
- Unweighted Pair Group Method with Arithmetic mean (UPGMA)
Pairwise distances (one obs.)
All pairwise distances
Centroid Method
- The centroid of a cluster can be defined as the mean of all the points in the cluster.
Centroid Method
- The centroid of a cluster can be defined as the mean of all the points in the cluster.
- If A is a cluster containing the observations a then the centroid of A is given by.
Centroid Method
- The centroid of a cluster can be defined as the mean of all the points in the cluster.
- If A is a cluster containing the observations a then the centroid of A is given by. ¯a=1|A|∑ai∈Aai
Centroid Method
- The centroid of a cluster can be defined as the mean of all the points in the cluster.
- If A is a cluster containing the observations a then the centroid of A is given by. ¯a=1|A|∑ai∈Aai
- The distance between two clusters can then be defined as the distance between the respective centroids.
Vector mean
- Recall that ai is a vector of attributes, e.g income and age.
Vector mean
- Recall that ai is a vector of attributes, e.g income and age.
- In this case ¯a is also a vector of attributes.
Vector mean
- Recall that ai is a vector of attributes, e.g income and age.
- In this case ¯a is also a vector of attributes.
- Each element of ¯a is the mean of a different attribute, e.g. mean income, mean age.
Centroid method
Centroid method
Average Linkage v Centroid
- Consider an example with one variable (although everything works with vectors too).
Average Linkage v Centroid
- Consider an example with one variable (although everything works with vectors too).
- Suppose we have the clusters A={0,2} and B={3,5}
Average Linkage v Centroid
- Consider an example with one variable (although everything works with vectors too).
- Suppose we have the clusters A={0,2} and B={3,5}
- Find the distance A and B using
Average Linkage v Centroid
- Consider an example with one variable (although everything works with vectors too).
- Suppose we have the clusters A={0,2} and B={3,5}
- Find the distance A and B using
- Average Linkage
- Centroid Method
Average Linkage
- Must find distances between all pairs of observations
Average Linkage
- Must find distances between all pairs of observations
- D(a1,b1)=3
- D(a1,b2)=5
- D(a2,b1)=1
- D(a2,b2)=3
Average Linkage
- Must find distances between all pairs of observations
- D(a1,b1)=3
- D(a1,b2)=5
- D(a2,b1)=1
- D(a2,b2)=3
- Averaging these, the distance is 3.
Centroid method
- First find centroids
Centroid method
- First find centroids
- ¯a=1
- ¯b=4
Centroid method
- First find centroids
- ¯a=1
- ¯b=4
- The distance is 3.
Centroid method
- First find centroids
- ¯a=1
- ¯b=4
- The distance is 3.
- Here both methods give the same answer but when vectors are used instead they do not give the same answer in general.
Average Linkage v Centroid
- In average linkage
Average Linkage v Centroid
- In average linkage
- Compute the distances between pairs of observations
- Average these distances
Average Linkage v Centroid
- In average linkage
- Compute the distances between pairs of observations
- Average these distances
- In the centroid method
Average Linkage v Centroid
- In average linkage
- Compute the distances between pairs of observations
- Average these distances
- In the centroid method
- Average the observations to obtain the centroid of each cluster.
- Find the distance between centroids
Ward's method
- All methods so far, merge two clusters when the distance between them is small.
Ward's method
- All methods so far, merge two clusters when the distance between them is small.
- Ward’s method merges two clusters to minimise within cluster variance.
Ward's method
- All methods so far, merge two clusters when the distance between them is small.
- Ward’s method merges two clusters to minimise within cluster variance.
- Two variations implemented in R.
Ward's method
- All methods so far, merge two clusters when the distance between them is small.
- Ward’s method merges two clusters to minimise within cluster variance.
- Two variations implemented in R.
Ward.D2is the same as the original Ward paper.Ward.Dis actually based on a mistake but can still work quite well.
Within Cluster Variance
- The within-cluster variance for a cluster A is defined as
Vw(A)=1|A|−1S(A)
where S(A)=∑ai∈A[(ai−¯a)′(ai−¯a)]
Vector notation
- The term S(A)=∑ai∈A(ai−¯a)′(ai−¯a) uses vector notation, but the idea is simple.
Vector notation
- The term S(A)=∑ai∈A(ai−¯a)′(ai−¯a) uses vector notation, but the idea is simple.
- Take the difference of each attribute from its mean (e.g. income, age, etc.)
Vector notation
- The term S(A)=∑ai∈A(ai−¯a)′(ai−¯a) uses vector notation, but the idea is simple.
- Take the difference of each attribute from its mean (e.g. income, age, etc.)
- Then square them and add together over attributes and observations.
Vector notation
- The term S(A)=∑ai∈A(ai−¯a)′(ai−¯a) uses vector notation, but the idea is simple.
- Take the difference of each attribute from its mean (e.g. income, age, etc.)
- Then square them and add together over attributes and observations.
- The within cluster variance is a total variance across all attributes.
Ward's algorithm
- At each step we must merge two clusters to form a single cluster.
Ward's algorithm
- At each step we must merge two clusters to form a single cluster.
- Suppose we pick a cluster A and B to form a new cluster C.
Ward's algorithm
- At each step we must merge two clusters to form a single cluster.
- Suppose we pick a cluster A and B to form a new cluster C.
- Ward's algorithm chooses A and B so that VW(C) is as small as possible.
Non-hierarchical Clustering
Non-hierarchical Clustering
- In some analyses the exact number of clusters may be known.
Non-hierarchical Clustering
- In some analyses the exact number of clusters may be known.
- If so non-hierachical clustering may be used.
Non-hierarchical Clustering
- In some analyses the exact number of clusters may be known.
- If so non-hierachical clustering may be used.
- Perhaps the most widely used non-hierarchical method is k-means clustering.
k-means
- In general k-means seeks to find k clusters.
k-means
- In general k-means seeks to find k clusters.
- The following condition must be satisfied:
k-means
- In general k-means seeks to find k clusters.
- The following condition must be satisfied:
- Each point in a must be closer to its own cluster centroid rather than the centroid of a different cluster.
k-means
- In general k-means seeks to find k clusters.
- The following condition must be satisfied:
- Each point in a must be closer to its own cluster centroid rather than the centroid of a different cluster.
- Knowing the partition into clusters determines the mean.
k-means
- In general k-means seeks to find k clusters.
- The following condition must be satisfied:
- Each point in a must be closer to its own cluster centroid rather than the centroid of a different cluster.
- Knowing the partition into clusters determines the mean.
- Knowing the means determines the clusters.
Optimality
- The objective of k-means clustering is to find centroids is a way that minimises within-cluster sum of squares.
Optimality
- The objective of k-means clustering is to find centroids is a way that minimises within-cluster sum of squares.
- Let C={C1,…,Ck} be a partitioning of all points into k clusters.
Optimality
- The objective of k-means clustering is to find centroids is a way that minimises within-cluster sum of squares.
- Let C={C1,…,Ck} be a partitioning of all points into k clusters.
- The objective of k-means is to find argminCk∑h=1S(Ch)
NP hard
- It is an example of an NP-hard problem
NP hard
- It is an example of an NP-hard problem
- The bad news is that NP-hard problems cannot be easily solved by computers.
NP hard
- It is an example of an NP-hard problem
- The bad news is that NP-hard problems cannot be easily solved by computers.
- The good news is that your credit card security also relies on the fact that computers cannot easily solve NP-hard problems.
Heuristic
- Fortunately there are algorithms that provide a reasonably good solution to the k-means problem.
Heuristic
- Fortunately there are algorithms that provide a reasonably good solution to the k-means problem.
- In some cases they may provide the exact solution, although there are no guarantees.
Heuristic
- Fortunately there are algorithms that provide a reasonably good solution to the k-means problem.
- In some cases they may provide the exact solution, although there are no guarantees.
- We will now cover Lloyd's algorithm which provides good intuition into the k-means problem.
Heuristic
- Fortunately there are algorithms that provide a reasonably good solution to the k-means problem.
- In some cases they may provide the exact solution, although there are no guarantees.
- We will now cover Lloyd's algorithm which provides good intuition into the k-means problem.
- By default, R implements the more sophisticated (and complicated) Hartigan Wong algorithm.
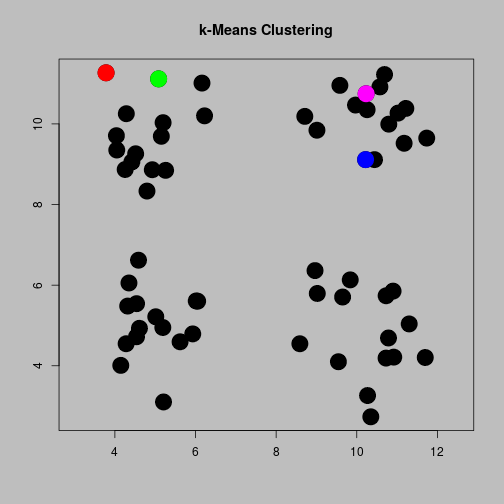
Lloyd's algorithm
- Choose initial centroids (possibly at random).
Lloyd's algorithm
- Choose initial centroids (possibly at random).
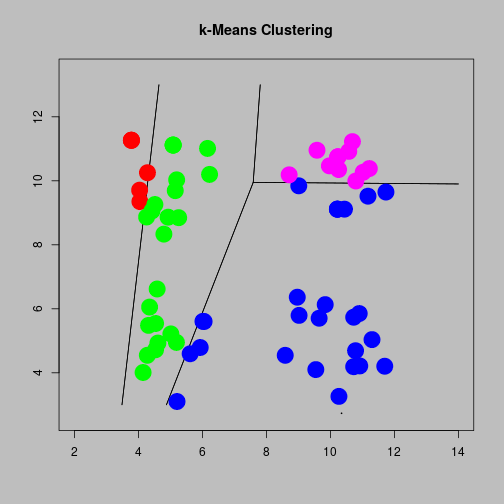
- Allocate each observation to cluster corresponding with nearest centroid
Lloyd's algorithm
- Choose initial centroids (possibly at random).
- Allocate each observation to cluster corresponding with nearest centroid
- Re-compute centroids as the mean of all observations in the cluster
Lloyd's algorithm
- Choose initial centroids (possibly at random).
- Allocate each observation to cluster corresponding with nearest centroid
- Re-compute centroids as the mean of all observations in the cluster
- Repeat steps 2 and 3 until convergence
Raw Data
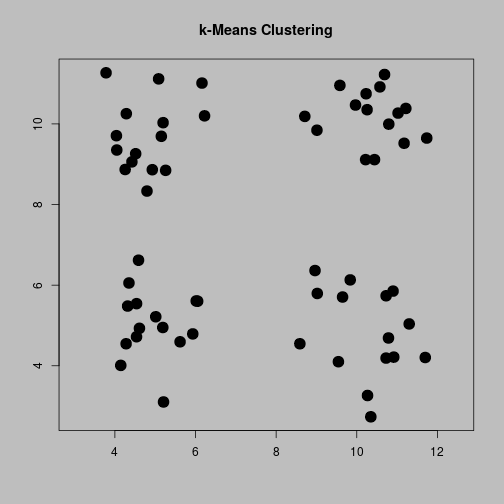
Initial Centroids
Initial Allocation
Re-compute Centroids
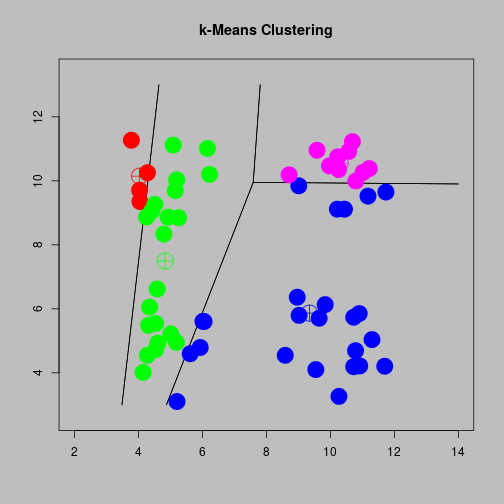
Reallocate
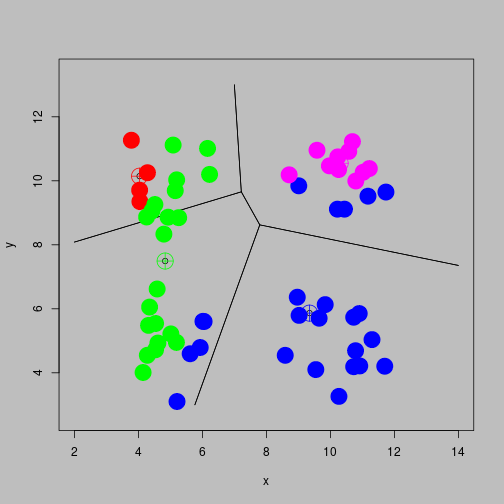
Reallocate
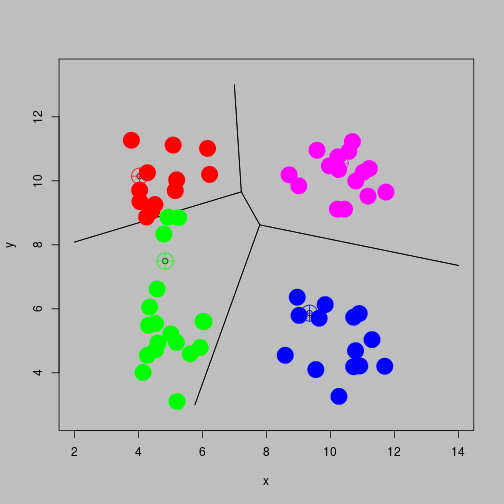
Recompute Centroids
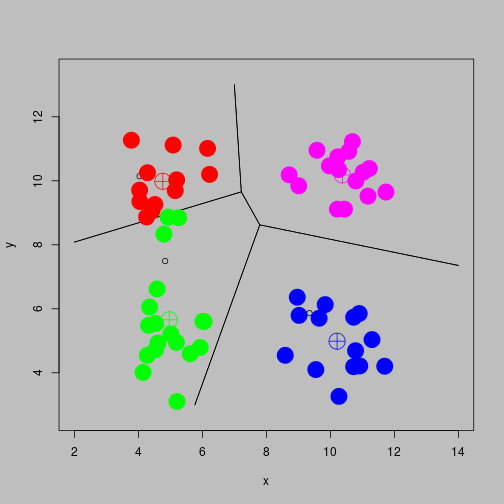
Reallocate
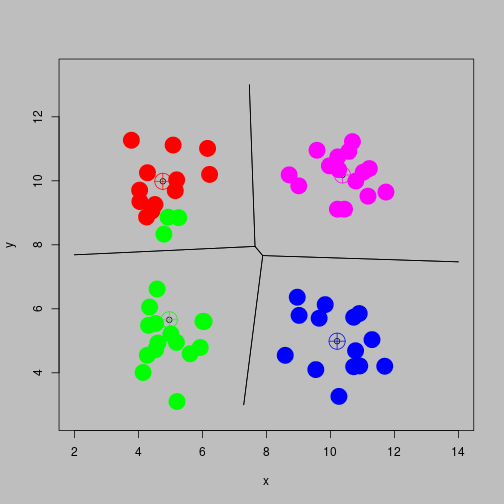
Reallocate
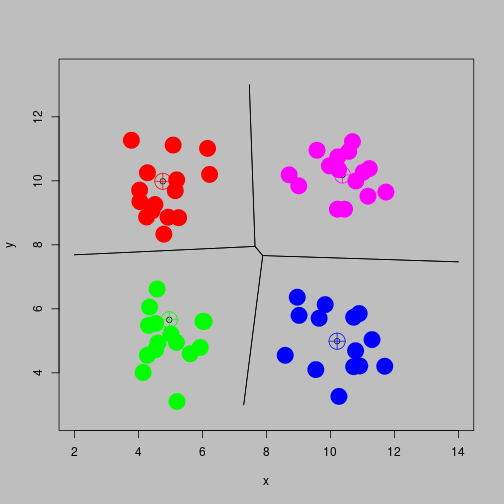
Stable solution
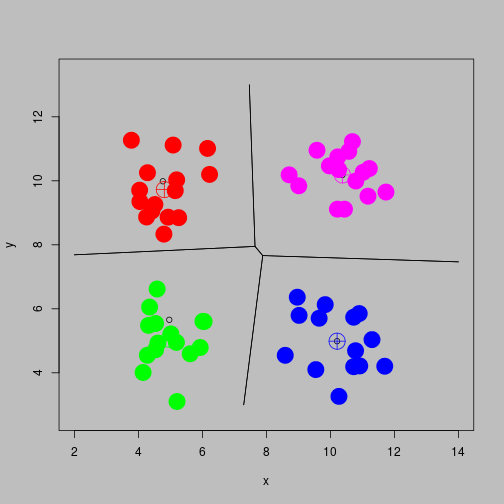
Wholesaler Data
- Recall the Wholesaler data from earlier in the lecture
Wholesaler Data
- Recall the Wholesaler data from earlier in the lecture
- The variables are annual spend in 6 categories.
Wholesaler Data
- Recall the Wholesaler data from earlier in the lecture
- The variables are annual spend in 6 categories.
- Should the data be standardised?
Wholesaler Data
- Recall the Wholesaler data from earlier in the lecture
- The variables are annual spend in 6 categories.
- Should the data be standardised?
- Try to carry out k means clustering using the R function
kmeans
Wholesaler Data
- Recall the Wholesaler data from earlier in the lecture
- The variables are annual spend in 6 categories.
- Should the data be standardised?
- Try to carry out k means clustering using the R function
kmeans - Find a solution with 3 clusters.
k-means in R
To do a three cluster solution
WholesaleCluster<-kmeans(Wholesale,3)If the data are in a data.frame you may need to select the numeric variables.
R output
- The result of the R function kmeans will be a list containing several entries. The most interesting are
R output
- The result of the R function kmeans will be a list containing
several entries. The most interesting are
- A variable indicating cluster membership is given in
cluster
- A variable indicating cluster membership is given in
R output
- The result of the R function kmeans will be a list containing
several entries. The most interesting are
- A variable indicating cluster membership is given in
cluster - The centroids for each cluster are given in
centers
- A variable indicating cluster membership is given in
R output
- The result of the R function kmeans will be a list containing
several entries. The most interesting are
- A variable indicating cluster membership is given in
cluster - The centroids for each cluster are given in
centers - The number of observations in each cluster is given by
size
- A variable indicating cluster membership is given in
R output
- The result of the R function kmeans will be a list containing
several entries. The most interesting are
- A variable indicating cluster membership is given in
cluster - The centroids for each cluster are given in
centers - The number of observations in each cluster is given by
size - The cluster centroids can be useful for profiling the clusters.
- A variable indicating cluster membership is given in
Cluster Centroids
| Fresh | Milk | Grocery | Frozen | Detergents_Paper | Delicassen |
|---|---|---|---|---|---|
| 8000.04 | 18511.420 | 27573.900 | 1996.680 | 12407.360 | 2252.020 |
| 35941.40 | 6044.450 | 6288.617 | 6713.967 | 1039.667 | 3049.467 |
| 8253.47 | 3824.603 | 5280.455 | 2572.661 | 1773.058 | 1137.497 |
Robustness Check
Since values are sensitive to starting values, we can run the algorithm with many different starting values using the nstart option
WholesaleCluster<-kmeans(Wholesale,3,nstart = 25)| Fresh | Milk | Grocery | Frozen | Detergents_Paper | Delicassen |
|---|---|---|---|---|---|
| 35941.40 | 6044.450 | 6288.617 | 6713.967 | 1039.667 | 3049.467 |
| 8000.04 | 18511.420 | 27573.900 | 1996.680 | 12407.360 | 2252.020 |
| 8253.47 | 3824.603 | 5280.455 | 2572.661 | 1773.058 | 1137.497 |
Label switching
- Two slides back the second cluster had the highest spend on fresh food.
Label switching
- Two slides back the second cluster had the highest spend on fresh food.
- One slide back the first cluster that had the highest spend on fresh food.
Label switching
- Two slides back the second cluster had the highest spend on fresh food.
- One slide back the first cluster that had the highest spend on fresh food.
- The centroids were identical, they were just flipped around. This is called Label switching.
Label switching
- Two slides back the second cluster had the highest spend on fresh food.
- One slide back the first cluster that had the highest spend on fresh food.
- The centroids were identical, they were just flipped around. This is called Label switching.
- It does not matter which cluster is first, second or third. The means are important.
Number of clusters
- The motivation of k means clustering is that the number of clusters is already known.
Number of clusters
- The motivation of k means clustering is that the number of clusters is already known.
- In principal different choices of k can be used and compared to one another.
Number of clusters
- The motivation of k means clustering is that the number of clusters is already known.
- In principal different choices of k can be used and compared to one another.
- However, unlike hierarchical clustering, these different solutions can contradict one another.
The meaning of non hierarchical
- Consider the two cluster solution (Solution A) and three cluster solution (Solution B) for hierarchical clustering.
The meaning of non hierarchical
- Consider the two cluster solution (Solution A) and three cluster solution (Solution B) for hierarchical clustering.
- If two variables are in the same cluster in Solution B then they will be in the same cluster in Solution A
The meaning of non hierarchical
- Consider the two cluster solution (Solution A) and three cluster solution (Solution B) for hierarchical clustering.
- If two variables are in the same cluster in Solution B then they will be in the same cluster in Solution A
- The same is not true for non-hierarchical clustering including k-means clustering.
Hierarchical Clustering
Together we will use Ward's method to do hierarchical clustering on the Wholesale data and get the cluster membership from the two and three cluster solutions.
Then you can try the same for k-means
Solution
Wholesale%>% dist%>% hclust(method='ward.D2')->hierclcl2<-cutree(hiercl,2)cl3<-cutree(hiercl,3)table(cl2,cl3)| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 261 | 0 | 45 |
| 2 | 0 | 134 | 0 |
Same exercise for k-means
km2<-kmeans(Wholesale,2)kmcl2<-km2$clusterkm3<-kmeans(Wholesale,3)kmcl3<-km3$clustertable(kmcl2,kmcl3)| 1 | 2 | 3 | |
|---|---|---|---|
| 1 | 0 | 59 | 6 |
| 2 | 330 | 1 | 44 |
Non-hierarchical
- Consider the observations in Cluster 3 when k=3. When we go from k=3 to k=2
Non-hierarchical
- Consider the observations in Cluster 3 when k=3. When we go from k=3 to k=2
- There are 6 of these observations that go to the new cluster 1.
Non-hierarchical
- Consider the observations in Cluster 3 when k=3. When we go from k=3 to k=2
- There are 6 of these observations that go to the new cluster 1.
- The remaining 44 observations go to the new cluster 2.
Non-hierarchical
- Consider the observations in Cluster 3 when k=3. When we go from k=3 to k=2
- There are 6 of these observations that go to the new cluster 1.
- The remaining 44 observations go to the new cluster 2.
- Notice that there is some label switching as well.
Comparing Cluster solutions
Comparing Cluster solutions
- A challenging aspect of cluster analysis is that it is difficult to evaluate a cluster solution.
Comparing Cluster solutions
- A challenging aspect of cluster analysis is that it is difficult to evaluate a cluster solution.
- In forecasting compare forecasts to outcomes.
Comparing Cluster solutions
- A challenging aspect of cluster analysis is that it is difficult to evaluate a cluster solution.
- In forecasting compare forecasts to outcomes.
- In regression look at goodness of fit.
Comparing Cluster solutions
- A challenging aspect of cluster analysis is that it is difficult to evaluate a cluster solution.
- In forecasting compare forecasts to outcomes.
- In regression look at goodness of fit.
- There is also very little theory to guide us.
Comparing Cluster solutions
- A challenging aspect of cluster analysis is that it is difficult to evaluate a cluster solution.
- In forecasting compare forecasts to outcomes.
- In regression look at goodness of fit.
- There is also very little theory to guide us.
- In regression we know least squares is BLUE under certain assumptions.
Comparing Cluster solutions
- A challenging aspect of cluster analysis is that it is difficult to evaluate a cluster solution.
- In forecasting compare forecasts to outcomes.
- In regression look at goodness of fit.
- There is also very little theory to guide us.
- In regression we know least squares is BLUE under certain assumptions.
- How do we choose a clustering algorithm?
Choosing a method
- There is no ideal method to do hierarchical clustering.
Choosing a method
- There is no ideal method to do hierarchical clustering.
- A good strategy is to try a few different methods.
Choosing a method
- There is no ideal method to do hierarchical clustering.
- A good strategy is to try a few different methods.
- If there is a clear structure in the data then most methods will give similar results.
- It is not unusual to find one method yielding very different results.
Choosing a method
- There is no ideal method to do hierarchical clustering.
- A good strategy is to try a few different methods.
- If there is a clear structure in the data then most methods will give similar results.
- It is not unusual to find one method yielding very different results.
- If all methods give vastly different results then perhaps there are no clear clusters in the data.
Robustness
- We can check if a clustering solution is robust to different algorithms.
Robustness
- We can check if a clustering solution is robust to different algorithms.
- For example if the centroid method, average linkage, Ward method and k-means all give similar clusters then we can be confident that the clusters are truly a feature of the data.
Robustness
- We can check if a clustering solution is robust to different algorithms.
- For example if the centroid method, average linkage, Ward method and k-means all give similar clusters then we can be confident that the clusters are truly a feature of the data.
- One way to evaluate this is to look at the Rand Index.
Rand Index
- Suppose we have two cluster solutions, Solution A and Solution B.
Rand Index
- Suppose we have two cluster solutions, Solution A and Solution B.
- Pick two observations at random x and y.
Rand Index
- Suppose we have two cluster solutions, Solution A and Solution B.
- Pick two observations at random x and y.
- x and y are in the same cluster in Solution A and the same cluster in Solution B
Rand Index
- Suppose we have two cluster solutions, Solution A and Solution B.
- Pick two observations at random x and y.
- x and y are in the same cluster in Solution A and the same cluster in Solution B
- x and y are in different clusters in Solution A and different clusters in Solution B
Rand Index
- Suppose we have two cluster solutions, Solution A and Solution B.
- Pick two observations at random x and y.
- x and y are in the same cluster in Solution A and the same cluster in Solution B
- x and y are in different clusters in Solution A and different clusters in Solution B
- x and y are in the same cluster in Solution A and the different cluster in Solution B
Rand Index
- Suppose we have two cluster solutions, Solution A and Solution B.
- Pick two observations at random x and y.
- x and y are in the same cluster in Solution A and the same cluster in Solution B
- x and y are in different clusters in Solution A and different clusters in Solution B
- x and y are in the same cluster in Solution A and the different cluster in Solution B
- x and y are in different clusters in Solution A and same clusters in Solution B
Rand Index
- Scenario 1 and scenario 2 both suggest that the cluster solutions are in agreement
Rand Index
- Scenario 1 and scenario 2 both suggest that the cluster solutions are in agreement
- Scenario 3 and scenario 4 both suggest that the cluster solutions are in disagreement
Rand Index
- Scenario 1 and scenario 2 both suggest that the cluster solutions are in agreement
- Scenario 3 and scenario 4 both suggest that the cluster solutions are in disagreement
- The Rand Index gives the probability of picking two observations at random that are in agreement.
Rand Index
- Scenario 1 and scenario 2 both suggest that the cluster solutions are in agreement
- Scenario 3 and scenario 4 both suggest that the cluster solutions are in disagreement
- The Rand Index gives the probability of picking two observations at random that are in agreement.
- The Rand Index lies between 0 and 1 and higher numbers indicate agreement.
Adjusted Rand Index
- Even if observations are clustered at random, there will still be some agreement due to chance.
Adjusted Rand Index
- Even if observations are clustered at random, there will still be some agreement due to chance.
- The adjusted Rand index is designed to be 0 if the level of agreement is equivalent to the case where clustering is done at random.
Adjusted Rand Index
- Even if observations are clustered at random, there will still be some agreement due to chance.
- The adjusted Rand index is designed to be 0 if the level of agreement is equivalent to the case where clustering is done at random.
- It is still only equal to 1 if the two clustering solutions are in perfect agreement.
Adjusted Rand Index
- Even if observations are clustered at random, there will still be some agreement due to chance.
- The adjusted Rand index is designed to be 0 if the level of agreement is equivalent to the case where clustering is done at random.
- It is still only equal to 1 if the two clustering solutions are in perfect agreement.
- The adjusted Rand Index can be computed using the
adjustedRandIndexfunction in the packagemclust
Conclusion
- There are many methods for clustering.
Conclusion
- There are many methods for clustering.
- For this reason a cluster analysis should be carried out carefully and transparently.
Conclusion
- There are many methods for clustering.
- For this reason a cluster analysis should be carried out carefully and transparently.
- Although we have focused on algorithms in the lecture, remember that the objective of cluster analysis is to explore the data.
Conclusion
- There are many methods for clustering.
- For this reason a cluster analysis should be carried out carefully and transparently.
- Although we have focused on algorithms in the lecture, remember that the objective of cluster analysis is to explore the data.
- As such remember to profile the clusters and to provide insight into what these clusters may represent.