Multidimensional Scaling
High Dimensional Data Analysis
Anastasios Panagiotelis & Ruben Loaiza-Maya
Lecture 5
Motivation
Motivation
- Previously we looked at the concept of distance between observations.
Motivation
- Previously we looked at the concept of distance between observations.
- We looked at our usual understanding of distance known as Euclidean distance.
Motivation
- Previously we looked at the concept of distance between observations.
- We looked at our usual understanding of distance known as Euclidean distance.
- We also looked at higher dimensional versions of Euclidean distance.
Motivation
- Previously we looked at the concept of distance between observations.
- We looked at our usual understanding of distance known as Euclidean distance.
- We also looked at higher dimensional versions of Euclidean distance.
- Other distance metrics including Jaccard distance can be used for categorical data.
Can we see distance?
- Suppose we have \(n\) observations and the distance between each possible pair of observations.
Can we see distance?
- Suppose we have \(n\) observations and the distance between each possible pair of observations.
- A scatterplot shows whether observations are close together or far apart.
Can we see distance?
- Suppose we have \(n\) observations and the distance between each possible pair of observations.
- A scatterplot shows whether observations are close together or far apart.
- This works nicely when there are 2 variables.
Higher-dimensional plots
- Suppose we have \(p\) variables where \(p\) is large.
Higher-dimensional plots
- Suppose we have \(p\) variables where \(p\) is large.
- Consider \(p\)-dimensional Euclidean distances.
Higher-dimensional plots
- Suppose we have \(p\) variables where \(p\) is large.
- Consider \(p\)-dimensional Euclidean distances.
- Can we represent these using just \(2\)-dimensions?
Higher-dimensional plots
- Suppose we have \(p\) variables where \(p\) is large.
- Consider \(p\)-dimensional Euclidean distances.
- Can we represent these using just \(2\)-dimensions?
- Unfortunately the answer is no...
Higher-dimensional plots
- Suppose we have \(p\) variables where \(p\) is large.
- Consider \(p\)-dimensional Euclidean distances.
- Can we represent these using just \(2\)-dimensions?
- Unfortunately the answer is no...
- ... but we can get a good approximation
Multidimensional Scaling
- Multidimensional scaling (MDS) finds a low (usually 2) dimensional representation.
Multidimensional Scaling
- Multidimensional scaling (MDS) finds a low (usually 2) dimensional representation.
- The pairwise 2D Euclidean distances in this representation should be as close as possible to the original distances.
Multidimensional Scaling
- Multidimensional scaling (MDS) finds a low (usually 2) dimensional representation.
- The pairwise 2D Euclidean distances in this representation should be as close as possible to the original distances.
- The meaning of close can vary since there are different ways to do MDS.
Multidimensional Scaling
- Multidimensional scaling (MDS) finds a low (usually 2) dimensional representation.
- The pairwise 2D Euclidean distances in this representation should be as close as possible to the original distances.
- The meaning of close can vary since there are different ways to do MDS.
- However MDS always begins with a matrix of distances and ends with a low dimensional representation that can be plotted.
An optical illusion with Beyonce

Why does the illusion work?
- The photo is a 2D representation of a 3D reality.
Why does the illusion work?
- The photo is a 2D representation of a 3D reality.
- In reality the distance between Beyonce's hand and the Eiffel Tower is large.
Why does the illusion work?
- The photo is a 2D representation of a 3D reality.
- In reality the distance between Beyonce's hand and the Eiffel Tower is large.
- In the 2D photo, this distance is small.
Why does the illusion work?
- The photo is a 2D representation of a 3D reality.
- In reality the distance between Beyonce's hand and the Eiffel Tower is large.
- In the 2D photo, this distance is small.
- This is a misleading representation to understand the distance between Beyonce's hand and the Eiffel Tower.
Why does the illusion work?
- The photo is a 2D representation of a 3D reality.
- In reality the distance between Beyonce's hand and the Eiffel Tower is large.
- In the 2D photo, this distance is small.
- This is a misleading representation to understand the distance between Beyonce's hand and the Eiffel Tower.
- A much more informative representation could be found by rotation.
Why do we care?
- An important issue in business is to profile the market. For example
Why do we care?
- An important issue in business is to profile the market. For
example
- Which products do customers perceive to be similar to one another?
Why do we care?
- An important issue in business is to profile the market. For
example
- Which products do customers perceive to be similar to one another?
- Who is my closest competitor?
Why do we care?
- An important issue in business is to profile the market. For
example
- Which products do customers perceive to be similar to one another?
- Who is my closest competitor?
- Are there ‘gaps’ in the market, where a new product can be introduced?
Why do we care?
- An important issue in business is to profile the market. For
example
- Which products do customers perceive to be similar to one another?
- Who is my closest competitor?
- Are there ‘gaps’ in the market, where a new product can be introduced?
- Multidimensional Scaling can help us to produce a simple visualisation that can address these questions.
Beer Example
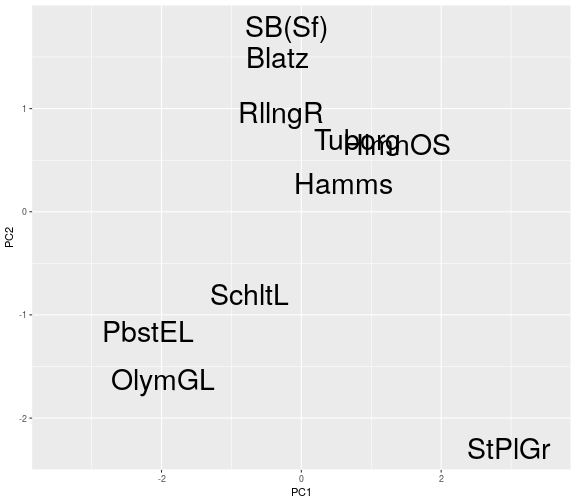
Beer Example
- The plot on the previous slide is an MDS solution for the beer dataset.
Beer Example
- The plot on the previous slide is an MDS solution for the beer dataset.
- The data are 5-dimensional so we cannot use a scatter plot.
Beer Example
- The plot on the previous slide is an MDS solution for the beer dataset.
- The data are 5-dimensional so we cannot use a scatter plot.
- MDS shows Olympia Gold Light and Pabst Extra Light are similar (both light beers).
Beer Example
- The plot on the previous slide is an MDS solution for the beer dataset.
- The data are 5-dimensional so we cannot use a scatter plot.
- MDS shows Olympia Gold Light and Pabst Extra Light are similar (both light beers).
- This also suggest that there is a low number of competitors with St Pauli Girl.
Beer Example
- The plot on the previous slide is an MDS solution for the beer dataset.
- The data are 5-dimensional so we cannot use a scatter plot.
- MDS shows Olympia Gold Light and Pabst Extra Light are similar (both light beers).
- This also suggest that there is a low number of competitors with St Pauli Girl.
- This may also reflect that the attributes of St Pauli Girl are not desired by customers.
Beer Example
- The plot on the previous slide is an MDS solution for the beer dataset.
- The data are 5-dimensional so we cannot use a scatter plot.
- MDS shows Olympia Gold Light and Pabst Extra Light are similar (both light beers).
- This also suggest that there is a low number of competitors with St Pauli Girl.
- This may also reflect that the attributes of St Pauli Girl are not desired by customers.
- How did we get the plot?
Beer Data
| beer | rating | origin | avail | price | cost | calories | sodium | alcohol | light |
|---|---|---|---|---|---|---|---|---|---|
| Olympia Gold Light | Fair | USA | Regional | 2.75 | 0.46 | 72 | 6 | 2.9 | LIGHT |
| Pabst Extra Light | Fair | USA | National | 2.29 | 0.38 | 68 | 15 | 2.3 | LIGHT |
| Schlitz Light | Fair | USA | National | 2.79 | 0.47 | 97 | 7 | 4.2 | LIGHT |
| Blatz | Fair | USA | Regional | 1.79 | 0.30 | 144 | 13 | 4.6 | NONLIGHT |
| Hamms | Fair | USA | Regional | 2.59 | 0.43 | 136 | 19 | 4.4 | NONLIGHT |
| Heilmans Old Style | Fair | USA | Regional | 2.59 | 0.43 | 144 | 24 | 4.9 | NONLIGHT |
| Rolling Rock | Fair | USA | Regional | 2.15 | 0.36 | 144 | 8 | 4.7 | NONLIGHT |
| Scotch Buy (Safeway) | Fair | USA | Regional | 1.59 | 0.27 | 145 | 18 | 4.5 | NONLIGHT |
| St Pauli Girl | Fair | Germany | Regional | 4.59 | 0.77 | 144 | 21 | 4.7 | NONLIGHT |
| Tuborg | Fair | USA | Regional | 2.59 | 0.43 | 155 | 13 | 5.0 | NONLIGHT |
Details
- To keep the example simple only the beers rated fair are used
Details
- To keep the example simple only the beers rated fair are used
- In general, all the beers can be used.
Details
- To keep the example simple only the beers rated fair are used
- In general, all the beers can be used.
- Also to keep things simple we only consider the metric variables so that we can use Euclidean distance.
Details
- To keep the example simple only the beers rated fair are used
- In general, all the beers can be used.
- Also to keep things simple we only consider the metric variables so that we can use Euclidean distance.
- In general, we can use distance metrics that work for categorical data.
Metric Variables
- After standardising, Euclidean distances are formed between every possible pair of beers.
Metric Variables
- After standardising, Euclidean distances are formed between every possible pair of beers.
- For example, the distance between Blatz and Tuborg is given by
Metric Variables
- After standardising, Euclidean distances are formed between every possible pair of beers.
- For example, the distance between Blatz and Tuborg is given by
$$\delta\left(\mbox{Blatz},\mbox{Tbrg}\right)=\sqrt{\sum\limits_{h=1}^5(\mbox{Blatz}_h-\mbox{Tbrg}_h)^2}$$ Both the notation \(\delta_{ij}\) and \(\delta(i,j)\) will be used interchangeably
Doing it in R
To obtain the distance matrix in R
filter(Beer,rating=='Fair')%>% #Only fair beers select_if(is.numeric)%>% #Only metric data scale%>% #Standardise dist->delta #Distancefilter(Beer,rating=='Fair')%>% #Only fair beers pull(beer)%>% #Get beer names abbreviate(6)-> #Abbreviate attributes(delta)$Labels #Assign to dMDS in R
We can do what is known as classical MDS in R using the cmdscale function
mdsout<-cmdscale(delta)| OlymGL | -1.9758212 | -1.6276821 |
| PbstEL | -2.1860282 | -1.1600914 |
| SchltL | -0.7420968 | -0.7994497 |
| Blatz | -0.3386684 | 1.4929936 |
| Hamms | 0.6053483 | 0.2720245 |
| HlmnOS | 1.3641181 | 0.6556403 |
| RllngR | -0.2932490 | 0.9661501 |
| SB(Sf) | -0.2067650 | 1.7951323 |
| StPlGr | 2.9648884 | -2.2976842 |
| Tuborg | 0.8082737 | 0.7029665 |
Two new variables
- We have just created two new variables for visualising the distances.
Two new variables
- We have just created two new variables for visualising the distances.
- The distances that we visualise will be 2-dimensional distances. For example
Two new variables
- We have just created two new variables for visualising the distances.
- The distances that we visualise will be 2-dimensional distances. For example
$$\begin{align}d&(\mbox{Blatz},\mbox{Tbrg})=\\&\sqrt{(-0.339-0.808)^2+(1.493-0.703)^2}\end{align}$$
Not exact
- In this example \(d(\mbox{Blatz},\mbox{Tuborg})=1.3927\) while \(\delta(\mbox{Blatz},\mbox{Tuborg})=1.4762\). Notice that
Not exact
- In this example \(d(\mbox{Blatz},\mbox{Tuborg})=1.3927\) while \(\delta(\mbox{Blatz},\mbox{Tuborg})=1.4762\). Notice that
$$ d(\mbox{Blatz},\mbox{Tuborg})\neq \delta(\mbox{Blatz},\mbox{Tuborg}) $$
- But they are close.
Getting the plot
mdsout%>% as_tibble%>% ggplot(aes(x=V1,y=V2))+geom_point()
Getting the plot with names
mdsout%>% as_tibble(rownames='BeerName')%>% ggplot(aes(x=V1,y=V2,label=BeerName))+geom_text()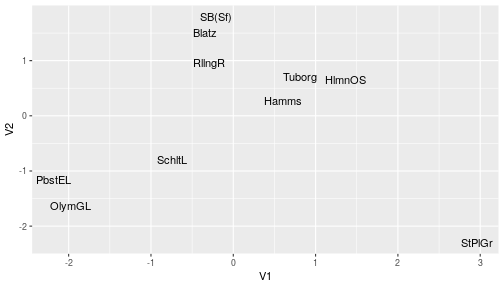
The math behind classical MDS
- In classical MDS the objective is to minimise strain
The math behind classical MDS
- In classical MDS the objective is to minimise strain
$$\mbox{Strain}=\sum\limits_{i=1}^{n-1}\sum\limits_{j>i}(\delta^2_{ij}-d^2_{ij})$$
- Note that the \(\delta_{ij}\) are high dimensional distances that come from the true data.
The math behind classical MDS
- In classical MDS the objective is to minimise strain
$$\mbox{Strain}=\sum\limits_{i=1}^{n-1}\sum\limits_{j>i}(\delta^2_{ij}-d^2_{ij})$$
- Note that the \(\delta_{ij}\) are high dimensional distances that come from the true data.
- The \(d_{ij}\) are low dimensional distances that come from the solution.
When can this be solved?
- The above problem has a tractable solution when Euclidean distance is used.
When can this be solved?
- The above problem has a tractable solution when Euclidean distance is used.
- This solution depends on an Eigenvalue decomposition.
When can this be solved?
- The above problem has a tractable solution when Euclidean distance is used.
- This solution depends on an Eigenvalue decomposition.
- This solution rotates the points until we get a 2D view that represents the true distances as accurately as possible.
Summary
- When Euclidean distance is used the solution provided by classical MDS:
Summary
- When Euclidean distance is used the solution provided by classical MDS:
- Minimises the strain.
Summary
- When Euclidean distance is used the solution provided by classical MDS:
- Minimises the strain.
- Results in eigenvalues that are all positive
Summary
- When Euclidean distance is used the solution provided by classical MDS:
- Minimises the strain.
- Results in eigenvalues that are all positive
- Can we use classical MDS when distances are non-Euclidean?
An example: Road distances
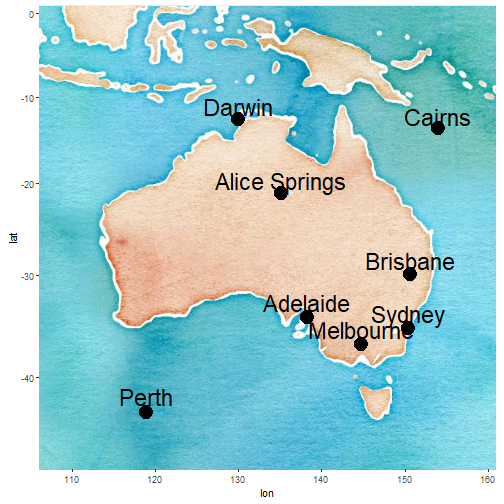
- Suppose that we have the road distances between different cities in Australia.
An example: Road distances
- Suppose that we have the road distances between different cities in Australia.
- The road distances are non-Euclidean since roads can be quite wiggly.
An example: Road distances
- Suppose that we have the road distances between different cities in Australia.
- The road distances are non-Euclidean since roads can be quite wiggly.
- We want to create a 2-dimensional map with the locations of the cities using only these road distances.
An example: Road distances
- Suppose that we have the road distances between different cities in Australia.
- The road distances are non-Euclidean since roads can be quite wiggly.
- We want to create a 2-dimensional map with the locations of the cities using only these road distances.
- Classical MDS can give an approximation that is quite close to a real map.
Road Distances
| Cairns | Brisbane | Sydney | Melbourne | Adelaide | Perth | Darwin | Alice Springs | |
|---|---|---|---|---|---|---|---|---|
| Cairns | 0 | 1717 | 2546 | 3054 | 3143 | 5954 | 2727 | 2324 |
| Brisbane | 1717 | 0 | 996 | 1674 | 2063 | 4348 | 3415 | 3012 |
| Sydney | 2546 | 996 | 0 | 868 | 1420 | 4144 | 4000 | 2644 |
| Melbourne | 3054 | 1674 | 868 | 0 | 728 | 3452 | 3781 | 2270 |
| Adelaide | 3143 | 2063 | 1420 | 728 | 0 | 2724 | 3053 | 1542 |
| Perth | 5954 | 4348 | 4144 | 3452 | 2724 | 0 | 4045 | 3630 |
| Darwin | 2727 | 3415 | 4000 | 3781 | 3053 | 4045 | 0 | 1511 |
| Alice Springs | 2324 | 3012 | 2644 | 2270 | 1542 | 3630 | 1511 | 0 |
Australia
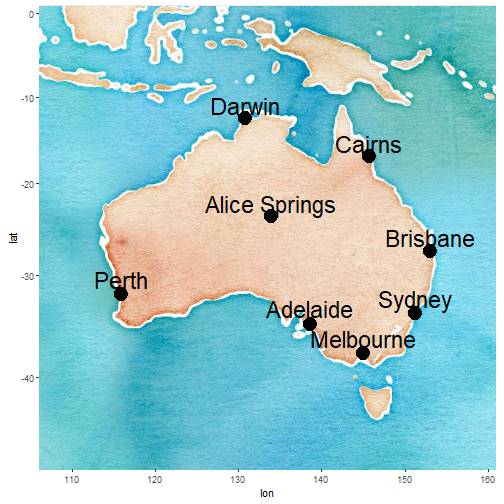
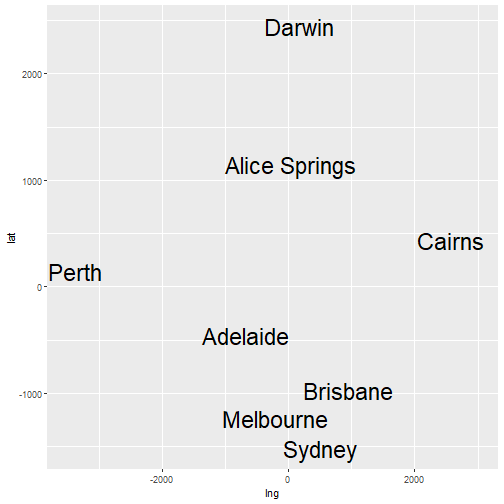
MDS Solution
Rotate
Back with Map
Rotating
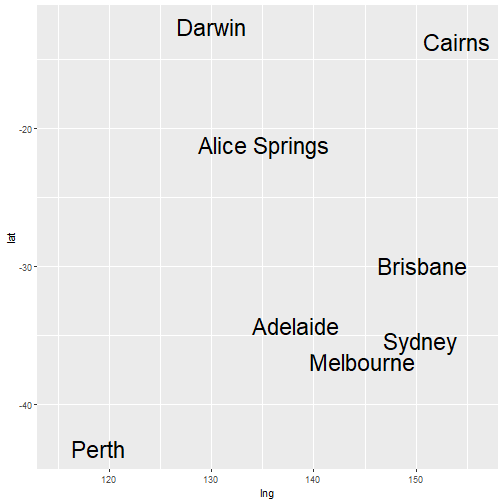
- Once a solution is available, we rotate the points within 2 dimensions.
Rotating
- Once a solution is available, we rotate the points within 2 dimensions.
- The 2D rotation does not change any of the distances.
Rotating
- Once a solution is available, we rotate the points within 2 dimensions.
- The 2D rotation does not change any of the distances.
- It can help us to interpret the axes.
Rotating
- Once a solution is available, we rotate the points within 2 dimensions.
- The 2D rotation does not change any of the distances.
- It can help us to interpret the axes.
- In the previous example the x-axis represents East-West direction and the y-axis represents North-South.
Evaluating MDS
How good is this representation?
- In theory, as long as the original distances are Euclidean, strain is minimised.
How good is this representation?
- In theory, as long as the original distances are Euclidean, strain is minimised.
- What if the optimal solution is still bad?
How good is this representation?
- In theory, as long as the original distances are Euclidean, strain is minimised.
- What if the optimal solution is still bad?
- Use two goodness of fit measures.
How good is this representation?
- In theory, as long as the original distances are Euclidean, strain is minimised.
- What if the optimal solution is still bad?
- Use two goodness of fit measures.
- Think of these in a similar fashion to R square in regression modelling.
Goodness of Fit Measures?
- These values depend on the eigenvalues $$\mbox{GF}_1=\frac{\sum\limits_{i=1}^2 |\lambda_i|}{\sum\limits^n_{i=1}|\lambda_i|}\, \mbox{GF}_2=\frac{\sum\limits_{i=1}^2 max(0,\lambda_i)}{\sum\limits^n_{i=1}max(0,\lambda_i)}$$
- For Euclidean distances \(\delta_{ij}\) eigenvalues are always positive and \(\mbox{GF}_1=\mbox{GF}_2\).
Beer Example
- In R obtain GoF using the option
eig=TRUEin thecmdscalefunction
Beer Example
- In R obtain GoF using the option
eig=TRUEin thecmdscalefunction - For the Beer data.
mdsout<-cmdscale(delta,eig=TRUE)str(mdsout$GOF)## num [1:2] 0.854 0.854GoF Measure
- You may notice that the GoF measures are the same.
GoF Measure
- You may notice that the GoF measures are the same.
- This is always the case when Euclidean distance is used.
GoF Measure
- You may notice that the GoF measures are the same.
- This is always the case when Euclidean distance is used.
- This arises since all eigenvalues are positive when the distance matrix is based on Euclidean distance.
Non-Euclidean distances
- In theory non-Euclidean distances can lead to negative eigenvalues. In this case:
Non-Euclidean distances
- In theory non-Euclidean distances can lead to negative eigenvalues. In this case:
- Classical MDS may not minimise Strain.
Non-Euclidean distances
- In theory non-Euclidean distances can lead to negative eigenvalues. In this case:
- Classical MDS may not minimise Strain.
- It minimises a slightly different function of the distances.
Non-Euclidean distances
- In theory non-Euclidean distances can lead to negative eigenvalues. In this case:
- Classical MDS may not minimise Strain.
- It minimises a slightly different function of the distances.
- Two fit measures will differ.
Non-Euclidean distances
- In theory non-Euclidean distances can lead to negative eigenvalues. In this case:
- Classical MDS may not minimise Strain.
- It minimises a slightly different function of the distances.
- Two fit measures will differ.
- Overall, we can use classical MDS for non-Euclidean distance but must be more careful.
Australia data
cmdscale(doz,eig=TRUE)->dozoutstr(dozout$eig)## num [1:8] 1.97e+07 1.25e+07 2.62e+06 5.96e+04 -3.26e-09 ...str(dozout$eig[6:8])## num [1:3] -311786 -1083294 -2179888str(dozout$GOF)## num [1:2] 0.837 0.923Evaluating the Result
- There are negative eigenvalues.
Evaluating the Result
- There are negative eigenvalues.
- This occurs since road distances are not Euclidean
Evaluating the Result
- There are negative eigenvalues.
- This occurs since road distances are not Euclidean
- This also implies that classical MDS does not minimise strain.
Evaluating the Result
- There are negative eigenvalues.
- This occurs since road distances are not Euclidean
- This also implies that classical MDS does not minimise strain.
- Both goodness of fit measures are quite high.
Evaluating the Result
- There are negative eigenvalues.
- This occurs since road distances are not Euclidean
- This also implies that classical MDS does not minimise strain.
- Both goodness of fit measures are quite high.
- The solution is an accurate representation.
Another example: Cheese
The following example comes from ‘Multidimensional Scaling of Sorting Data Applied to Cheese Perception’, Food Quality and Preference,6, pp.91-98. The purpose of this study was to visualise the difference between types of cheese.
Another example: Cheese
- The motivation is to investigate the similarities and differences between types of cheese.
Another example: Cheese
- The motivation is to investigate the similarities and differences between types of cheese.
- In principle one could measure attributes of the cheese.
Another example: Cheese
- The motivation is to investigate the similarities and differences between types of cheese.
- In principle one could measure attributes of the cheese.
- However the purpose of this study was to ask customers about their perceptions.
Another example: Cheese
- The motivation is to investigate the similarities and differences between types of cheese.
- In principle one could measure attributes of the cheese.
- However the purpose of this study was to ask customers about their perceptions.
- How do we ask customers about distances?
Another example: Cheese
- The motivation is to investigate the similarities and differences between types of cheese.
- In principle one could measure attributes of the cheese.
- However the purpose of this study was to ask customers about their perceptions.
- How do we ask customers about distances?
- Could you walk out on to the street and ask someone about the Euclidean distance between Brie and Camembert?
Constructing the Survey
- Customers can be asked:
Constructing the Survey
- Customers can be asked:
- On a scale of 1 to 10 with 1 being the most similar and 10 being the most different, how similar are the following cheeses
Constructing the Survey
- Customers can be asked:
- On a scale of 1 to 10 with 1 being the most similar and 10
being the most different, how similar are the following
cheeses
- Brie and Camembert
Constructing the Survey
- Customers can be asked:
- On a scale of 1 to 10 with 1 being the most similar and 10
being the most different, how similar are the following
cheeses
- Brie and Camembert
- Brie and Roquefort
Constructing the Survey
- Customers can be asked:
- On a scale of 1 to 10 with 1 being the most similar and 10
being the most different, how similar are the following
cheeses
- Brie and Camembert
- Brie and Roquefort
- Camembert and Roquefort
Constructing the Survey
- Customers can be asked:
- On a scale of 1 to 10 with 1 being the most similar and 10
being the most different, how similar are the following
cheeses
- Brie and Camembert
- Brie and Roquefort
- Camembert and Roquefort
- The dissimilarity scores can be averaged over all customers and used in an MDS
Constructing the Survey
- Customers can be asked:
- On a scale of 1 to 10 with 1 being the most similar and 10
being the most different, how similar are the following
cheeses
- Brie and Camembert
- Brie and Roquefort
- Camembert and Roquefort
- The dissimilarity scores can be averaged over all customers and used in an MDS
- This is not a good method when there is a large number of products.
A more feasible approach
- In the study there are 16 cheeses therefore 120 possible pairwise comparisons.
A more feasible approach
- In the study there are 16 cheeses therefore 120 possible pairwise comparisons.
- It is not practical to ask survey participants to make 120 comparisons!
A more feasible approach
- In the study there are 16 cheeses therefore 120 possible pairwise comparisons.
- It is not practical to ask survey participants to make 120 comparisons!
- Instead of being asked to make so many comparisons, customers were asked to put similar cheeses into groups.
A more feasible approach
- In the study there are 16 cheeses therefore 120 possible pairwise comparisons.
- It is not practical to ask survey participants to make 120 comparisons!
- Instead of being asked to make so many comparisons, customers were asked to put similar cheeses into groups.
- Proportion of customers with two cheeses in same group is a similarity score.
A more feasible approach
- In the study there are 16 cheeses therefore 120 possible pairwise comparisons.
- It is not practical to ask survey participants to make 120 comparisons!
- Instead of being asked to make so many comparisons, customers were asked to put similar cheeses into groups.
- Proportion of customers with two cheeses in same group is a similarity score.
- Proportion of customers with two cheeses in different groups is a dissimilarity score.
Consider four customers
- Suppose there are four customers sorting cheeses
Consider four customers
- Suppose there are four customers sorting cheeses
- Customer A: Brie and Camembert together, Roquefort and Blue Vein together
Consider four customers
- Suppose there are four customers sorting cheeses
- Customer A: Brie and Camembert together, Roquefort and Blue Vein together
- Customer B: Roquefort and Blue Vein together, all others separate
Consider four customers
- Suppose there are four customers sorting cheeses
- Customer A: Brie and Camembert together, Roquefort and Blue Vein together
- Customer B: Roquefort and Blue Vein together, all others separate
- Customer C: All cheeses in their own category
Consider four customers
- Suppose there are four customers sorting cheeses
- Customer A: Brie and Camembert together, Roquefort and Blue Vein together
- Customer B: Roquefort and Blue Vein together, all others separate
- Customer C: All cheeses in their own category
- Customer D: All cheeses in one category
Comparisons
- Customer A and D have Brie and Camembert in the same group, customers B and C have them in different groups.
Comparisons
- Customer A and D have Brie and Camembert in the same group, customers B and C have them in different groups.
- The distance between Brie and Camembert is 0.5.
Comparisons
- Customer A and D have Brie and Camembert in the same group, customers B and C have them in different groups.
- The distance between Brie and Camembert is 0.5.
- Customer A, B and D have Roquefort and Blue Vein in the same group, customer C has them in different groups.
Comparisons
- Customer A and D have Brie and Camembert in the same group, customers B and C have them in different groups.
- The distance between Brie and Camembert is 0.5.
- Customer A, B and D have Roquefort and Blue Vein in the same group, customer C has them in different groups.
- The distance between Roquefort and Blue Vein is 0.25.
MDS
- The study on cheese did not use classical MDS but something called Kruskals algorithm.
- There are many alternatives to classical MDS.
- We now briefly cover some of the ideas behind them.
Beyond Classical MDS
Beyond Classical MDS
- Classical MDS is designed to minimise Strain.
Beyond Classical MDS
- Classical MDS is designed to minimise Strain.
- An alternative objective function called Stress can be minimised instead
Beyond Classical MDS
- Classical MDS is designed to minimise Strain.
- An alternative objective function called Stress can be minimised instead
$$\mbox{Stress}=\sum\limits_{i=1}^{n-1}\sum\limits_{j>i}\frac{(\delta_{ij}-d_{ij})^2}{\delta_{ij}}$$
Beyond Classical MDS
- Classical MDS is designed to minimise Strain.
- An alternative objective function called Stress can be minimised instead
$$\mbox{Stress}=\sum\limits_{i=1}^{n-1}\sum\limits_{j>i}\frac{(\delta_{ij}-d_{ij})^2}{\delta_{ij}}$$
- The difference between \(\delta_{ij}\) and \(d_{ij}\) acts like an error.
Beyond Classical MDS
- Classical MDS is designed to minimise Strain.
- An alternative objective function called Stress can be minimised instead
$$\mbox{Stress}=\sum\limits_{i=1}^{n-1}\sum\limits_{j>i}\frac{(\delta_{ij}-d_{ij})^2}{\delta_{ij}}$$
- The difference between \(\delta_{ij}\) and \(d_{ij}\) acts like an error.
- The \(\delta_{ij}\) on the denominator acts as a weight
Weighting
- For large \(\delta\) observations are far away in the original space.
Weighting
- For large \(\delta\) observations are far away in the original space.
- For these pairs errors are more easily tolerated.
Weighting
- For large \(\delta\) observations are far away in the original space.
- For these pairs errors are more easily tolerated.
- For small \(\delta\) observations are close in the original space.
Weighting
- For large \(\delta\) observations are far away in the original space.
- For these pairs errors are more easily tolerated.
- For small \(\delta\) observations are close in the original space.
- For these pairs errors are not tolerated.
Weighting
- For large \(\delta\) observations are far away in the original space.
- For these pairs errors are more easily tolerated.
- For small \(\delta\) observations are close in the original space.
- For these pairs errors are not tolerated.
- The most accuracy is achieved for nearby points
Weighting
- For large \(\delta\) observations are far away in the original space.
- For these pairs errors are more easily tolerated.
- For small \(\delta\) observations are close in the original space.
- For these pairs errors are not tolerated.
- The most accuracy is achieved for nearby points
- The local structure is preserved.
Sammon mapping
- The Sammon mapping is solved by numerical optimisation.
Sammon mapping
- The Sammon mapping is solved by numerical optimisation.
- It is different from the classical solution
Sammon mapping
- The Sammon mapping is solved by numerical optimisation.
- It is different from the classical solution
- It is not based on an eigenvalue decomposition
Sammon mapping
- The Sammon mapping is solved by numerical optimisation.
- It is different from the classical solution
- It is not based on an eigenvalue decomposition
- It is not based on rotation
Sammon mapping
- The Sammon mapping is solved by numerical optimisation.
- It is different from the classical solution
- It is not based on an eigenvalue decomposition
- It is not based on rotation
- It is a non-linear mapping.
Example
- Consider the case where points are in 2D space and the aim is to summarise them in 1D space (across a line).
- The specific problem of doing multidimensional scaling where the lower dimension is 1 is called seriation.
- It provides a ranking of the observations.
Example
- Consider the case where points are in 2D space and the aim is to summarise them in 1D space (across a line).
- The specific problem of doing multidimensional scaling where the lower dimension is 1 is called seriation.
- It provides a ranking of the observations.
- In marketing it can be used to elicit preferences.
Original Data
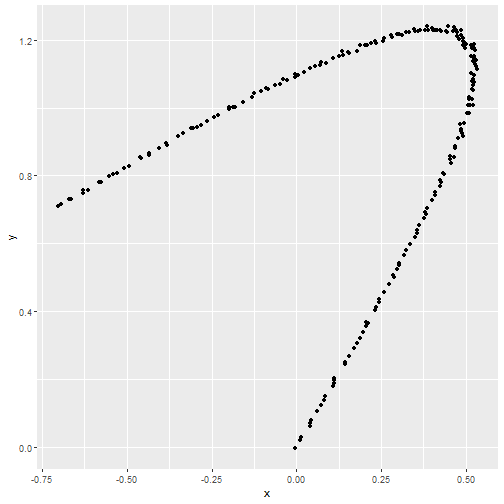
Original Data
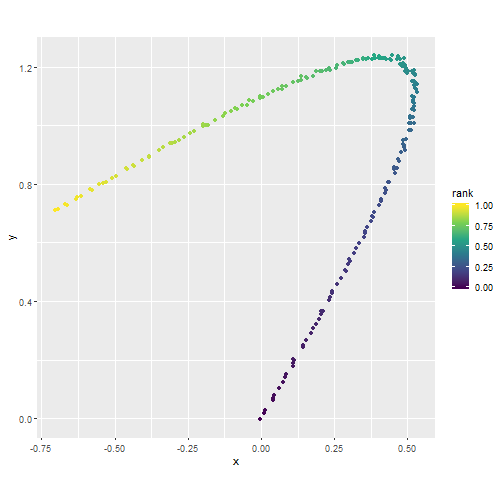
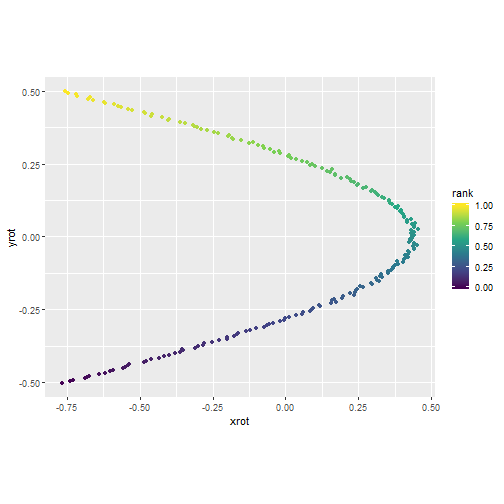
Rotate (Classical Solution)
Keep 1 Dimension
Rug plot (classical solution)
Sammon Mapping
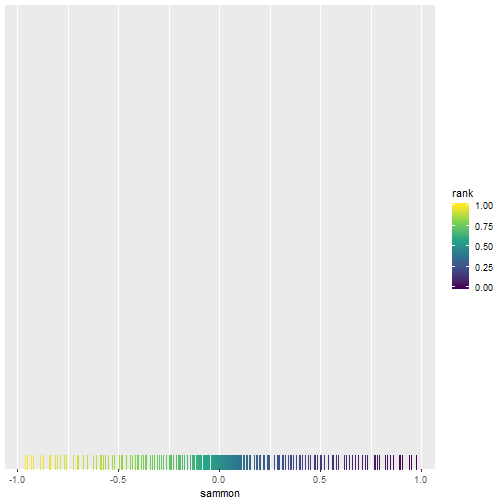
Discussion
- Classical MDS cannot account for non-linearity.
- The dark blue and yellow points are represented as close to one another.
- Sammon does account for non-linearity.
- The blue and yellow points are represented as far apart.
- Although they are not so far apart in the original space, these observations are downweighted relative to the local structure.
Kruskal algorithm
- Kruskal's algorithm minimises a slightly different criterion.
Kruskal algorithm
- Kruskal's algorithm minimises a slightly different criterion.
- This is still often called stress, which is admittedly confusing.
Kruskal algorithm
- Kruskal's algorithm minimises a slightly different criterion.
- This is still often called stress, which is admittedly confusing.
- Kruskal's algorithm is implemented in R using the
isoMDSfunction from theMASSpackage.
Monotone tranformations
- Kruskal's algorithm is invariant to monotone transformations of the distances.
Monotone tranformations
- Kruskal's algorithm is invariant to monotone transformations of the distances.
- By monotone transformation we mean any function of the distance that is either constantly increasing or decreasing.
Monotone tranformations
- Kruskal's algorithm is invariant to monotone transformations of the distances.
- By monotone transformation we mean any function of the distance that is either constantly increasing or decreasing.
- Exponential function is monotone
Monotone tranformations
- Kruskal's algorithm is invariant to monotone transformations of the distances.
- By monotone transformation we mean any function of the distance that is either constantly increasing or decreasing.
- Exponential function is monotone
- Sine function is not monotone
Monotone tranformations
- Kruskal's algorithm is invariant to monotone transformations of the distances.
- By monotone transformation we mean any function of the distance that is either constantly increasing or decreasing.
- Exponential function is monotone
- Sine function is not monotone
- By invariant we mean that the solution provided by Kruskal's does not change if we transform the input distances.
Example
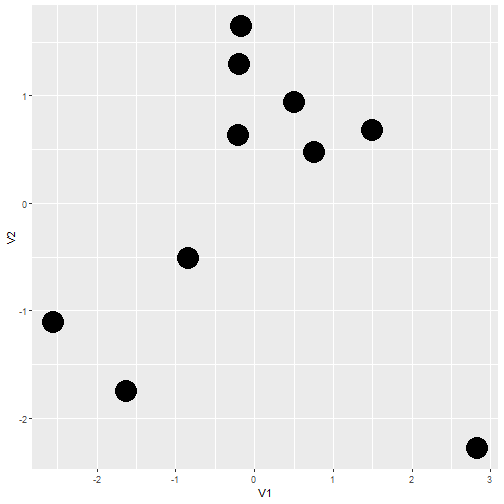
library(MASS)isoMDS(d)->kBeer## initial value 9.127089 ## iter 5 value 5.688460## final value 5.611143 ## convergedMake plot
kBeer$points%>% as_tibble()%>% ggplot(aes(x=V1,y=V2))+ geom_point(size=10)Make plot
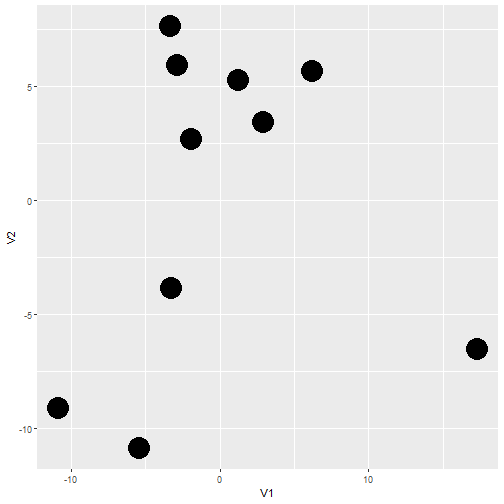
Squared distances
isoMDS(d^2)->kBeer2## initial value 11.274285 ## iter 5 value 6.447929## iter 10 value 5.697285## final value 5.603035 ## convergedSolution
Comparison
- Squaring the distances provides the same solution with two caveats:
Comparison
- Squaring the distances provides the same solution with two caveats:
- The stress is slightly different. Numerical optimisation can vary a little depending on starting values.
Comparison
- Squaring the distances provides the same solution with two caveats:
- The stress is slightly different. Numerical optimisation can vary a little depending on starting values.
- The points in one plot are slightly rotated compared to the other.
Comparison
- Squaring the distances provides the same solution with two caveats:
- The stress is slightly different. Numerical optimisation can vary a little depending on starting values.
- The points in one plot are slightly rotated compared to the other.
- Why is the invariance to monotone tranformations important?
Non metric MDS
- In some cases, the distance themselves are not metric but ordinal.
Non metric MDS
- In some cases, the distance themselves are not metric but ordinal.
- Suppose we only know
Non metric MDS
- In some cases, the distance themselves are not metric but ordinal.
- Suppose we only know $$\delta_{\mbox{Bri.},\mbox{Cam.}}< \delta_{\mbox{Roq.},\mbox{Cam.}}< \delta_{\mbox{Roq.},\mbox{Bri.}}$$
Non metric MDS
- In some cases, the distance themselves are not metric but ordinal.
- Suppose we only know $$\delta_{\mbox{Bri.},\mbox{Cam.}}< \delta_{\mbox{Roq.},\mbox{Cam.}}< \delta_{\mbox{Roq.},\mbox{Bri.}}$$
- Brie and Roquefort are more different compared to Brie and Camembert.
Non metric MDS
- In some cases, the distance themselves are not metric but ordinal.
- Suppose we only know $$\delta_{\mbox{Bri.},\mbox{Cam.}}< \delta_{\mbox{Roq.},\mbox{Cam.}}< \delta_{\mbox{Roq.},\mbox{Bri.}}$$
- Brie and Roquefort are more different compared to Brie and Camembert.
- We do not know how big the distance between Brie and Roquefort is compared to the distance between Brie and Camembert.
Non-metric MDS
- In this case we minimise Stress subject to constraints, e.g.
Non-metric MDS
- In this case we minimise Stress subject to constraints, e.g. $$\hat{\delta}_{\mbox{Bri.},\mbox{Cam.}}< \hat{\delta}_{\mbox{Roq.},\mbox{Cam.}}< \hat{\delta}_{\mbox{Roq.},\mbox{Bri.}}$$
Non-metric MDS
- Taking the ranks is an example of a monotone transformation.
Non-metric MDS
- Taking the ranks is an example of a monotone transformation.
- Therefore the solution of isoMDS only requires the ranks of the distances and not the distances themselves.
Non-metric MDS
- Taking the ranks is an example of a monotone transformation.
- Therefore the solution of isoMDS only requires the ranks of the distances and not the distances themselves.
- This is a very useful algorithm for marketing since survey participants cannot easily and reliable assign numbers to the difference between products.
Modern MDS
- Methods for finding a low dimensional representation of high-dimensional data continue to be used today
Modern MDS
- Methods for finding a low dimensional representation of high-dimensional data continue to be used today
- These mostly go by the name of manifold learning methods
Modern MDS
- Methods for finding a low dimensional representation of high-dimensional data continue to be used today
- These mostly go by the name of manifold learning methods
- They are not only used for visualisation
Modern MDS
- Methods for finding a low dimensional representation of high-dimensional data continue to be used today
- These mostly go by the name of manifold learning methods
- They are not only used for visualisation
- The low-dimensional co-ordinates can also be used as features in classification and regression.
Examples
- Local Linear Embedding (LLE)
- IsoMap
- Laplacian Eigenmap
- t SNE
- Kohonen Map
- ...
Examples
- Local Linear Embedding (LLE)
- IsoMap
- Laplacian Eigenmap
- t SNE
- Kohonen Map
- ...
- ... and others.
Properties
- For most of the modern methods two characteristics are common.
Properties
- For most of the modern methods two characteristics are common.
- The idea that local structure should be preserved. The first step of many algorithms is to find nearest neighbours of each point.
Properties
- For most of the modern methods two characteristics are common.
- The idea that local structure should be preserved. The first step of many algorithms is to find nearest neighbours of each point.
- In many algorithms an eigenvalue decomposition forms part of the solution as is the case in classic MDS.