Principal Components Analysis
High Dimensional Data Analysis
Anastasios Panagiotelis & Ruben Loaiza-Maya
Lecture 6
1
Motivation
2
High Dimensional Data
- In marketing surveys we may ask a large number of questions about customer experience.
3
High Dimensional Data
- In marketing surveys we may ask a large number of questions about customer experience.
- In finance there may be several ways to assess the credit worthiness of firms.
3
High Dimensional Data
- In marketing surveys we may ask a large number of questions about customer experience.
- In finance there may be several ways to assess the credit worthiness of firms.
- In economics the development of a country or state can be measured in different ways.
3
A real example
- Consider a dataset with the following variables for the 50 States of the USA
4
A real example
- Consider a dataset with the following variables for the 50 States of the USA
- Income
- Illiteracy
- Life Expectancy
- Murder Rate
- High School Graduation Rate
4
A real example
- Consider a dataset with the following variables for the 50 States of the USA
- Income
- Illiteracy
- Life Expectancy
- Murder Rate
- High School Graduation Rate
- You can access this via moodle from the file StateSE.rds
4
Summarising many variables
- Often we aim to combine many variables into a single index
5
Summarising many variables
- Often we aim to combine many variables into a single index
- In finance a credit score summarises all the information about the likelihood of bankruptcy for a company.
5
Summarising many variables
- Often we aim to combine many variables into a single index
- In finance a credit score summarises all the information about the likelihood of bankruptcy for a company.
- In marketing we require a single overall measure of customer experience.
5
Summarising many variables
- Often we aim to combine many variables into a single index
- In finance a credit score summarises all the information about the likelihood of bankruptcy for a company.
- In marketing we require a single overall measure of customer experience.
- In economics the Human Development Index is a single measure that takes income, education and health into account.
5
Weighted linear combination
- A convenient way to combine variables is through a linear combination (LC)
6
Weighted linear combination
- A convenient way to combine variables is through a linear combination (LC)
- For example, your grade for this unit: w1Assign. Marks+w2Exam Mark
- Here w1 and w2 are called weights
- In this unit, the weight for the Assignments is 50% and for the Examination is 50%
6
Weighted linear combination
- A convenient way to combine variables is through a linear combination (LC)
- For example, your grade for this unit: w1Assign. Marks+w2Exam Mark
- Here w1 and w2 are called weights
- In this unit, the weight for the Assignments is 50% and for the Examination is 50%
- What is a good way to choose weights?
6
Maximise variance
- The purpose of grading students is to differentiate the best perfoming students from the weakest performing students
7
Maximise variance
- The purpose of grading students is to differentiate the best perfoming students from the weakest performing students
- The index should have large variance.
7
Maximise variance
- The purpose of grading students is to differentiate the best perfoming students from the weakest performing students
- The index should have large variance.
- The LC with the highest variance is the first Principal Component of the data.
7
Maximise variance
- The purpose of grading students is to differentiate the best perfoming students from the weakest performing students
- The index should have large variance.
- The LC with the highest variance is the first Principal Component of the data.
- The first principal component is a new variable that explains as much variance as possible in the original variables.
7
Original Data
| State | Income | Illiteracy | LifeExp | Murder | HSGrad | StateAbb |
|---|---|---|---|---|---|---|
| Alabama | 3624 | 2.1 | 69.05 | 15.1 | 41.3 | AL |
| Alaska | 6315 | 1.5 | 69.31 | 11.3 | 66.7 | AK |
| Arizona | 4530 | 1.8 | 70.55 | 7.8 | 58.1 | AZ |
| Arkansas | 3378 | 1.9 | 70.66 | 10.1 | 39.9 | AR |
| California | 5114 | 1.1 | 71.71 | 10.3 | 62.6 | CA |
| Colorado | 4884 | 0.7 | 72.06 | 6.8 | 63.9 | CO |
| Connecticut | 5348 | 1.1 | 72.48 | 3.1 | 56.0 | CT |
| Delaware | 4809 | 0.9 | 70.06 | 6.2 | 54.6 | DE |
| Florida | 4815 | 1.3 | 70.66 | 10.7 | 52.6 | FL |
| Georgia | 4091 | 2.0 | 68.54 | 13.9 | 40.6 | GA |
| Hawaii | 4963 | 1.9 | 73.60 | 6.2 | 61.9 | HI |
| Idaho | 4119 | 0.6 | 71.87 | 5.3 | 59.5 | ID |
| Illinois | 5107 | 0.9 | 70.14 | 10.3 | 52.6 | IL |
| Indiana | 4458 | 0.7 | 70.88 | 7.1 | 52.9 | IN |
| Iowa | 4628 | 0.5 | 72.56 | 2.3 | 59.0 | IA |
| Kansas | 4669 | 0.6 | 72.58 | 4.5 | 59.9 | KS |
| Kentucky | 3712 | 1.6 | 70.10 | 10.6 | 38.5 | KY |
| Louisiana | 3545 | 2.8 | 68.76 | 13.2 | 42.2 | LA |
| Maine | 3694 | 0.7 | 70.39 | 2.7 | 54.7 | ME |
| Maryland | 5299 | 0.9 | 70.22 | 8.5 | 52.3 | MD |
| Massachusetts | 4755 | 1.1 | 71.83 | 3.3 | 58.5 | MA |
| Michigan | 4751 | 0.9 | 70.63 | 11.1 | 52.8 | MI |
| Minnesota | 4675 | 0.6 | 72.96 | 2.3 | 57.6 | MN |
| Mississippi | 3098 | 2.4 | 68.09 | 12.5 | 41.0 | MS |
| Missouri | 4254 | 0.8 | 70.69 | 9.3 | 48.8 | MO |
| Montana | 4347 | 0.6 | 70.56 | 5.0 | 59.2 | MT |
| Nebraska | 4508 | 0.6 | 72.60 | 2.9 | 59.3 | NE |
| Nevada | 5149 | 0.5 | 69.03 | 11.5 | 65.2 | NV |
| New Hampshire | 4281 | 0.7 | 71.23 | 3.3 | 57.6 | NH |
| New Jersey | 5237 | 1.1 | 70.93 | 5.2 | 52.5 | NJ |
| New Mexico | 3601 | 2.2 | 70.32 | 9.7 | 55.2 | NM |
| New York | 4903 | 1.4 | 70.55 | 10.9 | 52.7 | NY |
| North Carolina | 3875 | 1.8 | 69.21 | 11.1 | 38.5 | NC |
| North Dakota | 5087 | 0.8 | 72.78 | 1.4 | 50.3 | ND |
| Ohio | 4561 | 0.8 | 70.82 | 7.4 | 53.2 | OH |
| Oklahoma | 3983 | 1.1 | 71.42 | 6.4 | 51.6 | OK |
| Oregon | 4660 | 0.6 | 72.13 | 4.2 | 60.0 | OR |
| Pennsylvania | 4449 | 1.0 | 70.43 | 6.1 | 50.2 | PA |
| Rhode Island | 4558 | 1.3 | 71.90 | 2.4 | 46.4 | RI |
| South Carolina | 3635 | 2.3 | 67.96 | 11.6 | 37.8 | SC |
| South Dakota | 4167 | 0.5 | 72.08 | 1.7 | 53.3 | SD |
| Tennessee | 3821 | 1.7 | 70.11 | 11.0 | 41.8 | TN |
| Texas | 4188 | 2.2 | 70.90 | 12.2 | 47.4 | TX |
| Utah | 4022 | 0.6 | 72.90 | 4.5 | 67.3 | UT |
| Vermont | 3907 | 0.6 | 71.64 | 5.5 | 57.1 | VT |
| Virginia | 4701 | 1.4 | 70.08 | 9.5 | 47.8 | VA |
| Washington | 4864 | 0.6 | 71.72 | 4.3 | 63.5 | WA |
| West Virginia | 3617 | 1.4 | 69.48 | 6.7 | 41.6 | WV |
| Wisconsin | 4468 | 0.7 | 72.48 | 3.0 | 54.5 | WI |
| Wyoming | 4566 | 0.6 | 70.29 | 6.9 | 62.9 | WY |
8
First PC
| State | .fittedPC1 |
|---|---|
| Alabama | -3.4736429 |
| Alaska | 0.5523458 |
| Arizona | -0.3218179 |
| Arkansas | -2.3518240 |
| California | 0.9138319 |
| Colorado | 1.7319349 |
| Connecticut | 1.8293070 |
| Delaware | 0.3708443 |
| Florida | -0.4071974 |
| Georgia | -3.2000232 |
| Hawaii | 1.3275139 |
| Idaho | 1.2443096 |
| Illinois | -0.0586612 |
| Indiana | 0.4059830 |
| Iowa | 2.1960892 |
| Kansas | 1.9256885 |
| Kentucky | -2.2652570 |
| Louisiana | -3.8826563 |
| Maine | 0.4547571 |
| Maryland | 0.2844478 |
| Massachusetts | 1.3868972 |
| Michigan | -0.1768465 |
| Minnesota | 2.2025281 |
| Mississippi | -4.0362219 |
| Missouri | -0.3652702 |
| Montana | 0.9359256 |
| Nebraska | 2.0060961 |
| Nevada | 0.4719808 |
| New Hampshire | 1.1727342 |
| New Jersey | 0.7618589 |
| New Mexico | -1.6465196 |
| New York | -0.4937635 |
| North Carolina | -2.7036034 |
| North Dakota | 1.9049237 |
| Ohio | 0.3444655 |
| Oklahoma | 0.0227251 |
| Oregon | 1.8066483 |
| Pennsylvania | -0.0242343 |
| Rhode Island | 0.5548203 |
| South Carolina | -3.7722712 |
| South Dakota | 1.5131049 |
| Tennessee | -2.1379510 |
| Texas | -1.8743614 |
| Utah | 2.0995090 |
| Vermont | 0.8805572 |
| Virginia | -0.8810536 |
| Washington | 1.9687535 |
| West Virginia | -1.7131805 |
| Wisconsin | 1.5728437 |
| Wyoming | 0.9429316 |
9
First PC on Map
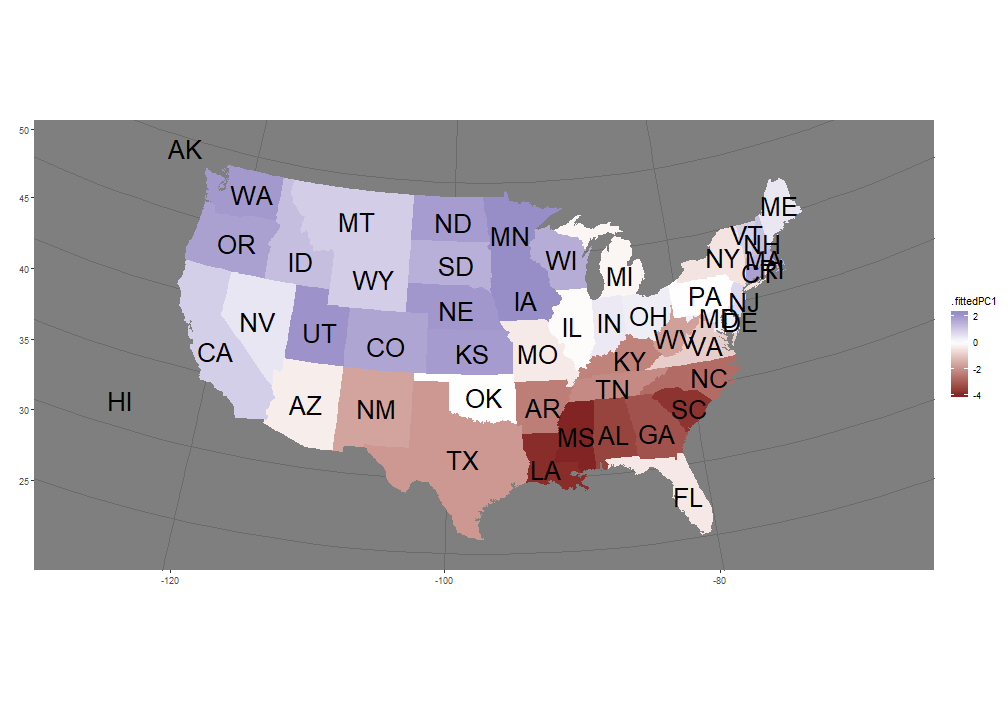
10
Second Principal Component
- Sometimes a single index still oversimplifies the data.
11
Second Principal Component
- Sometimes a single index still oversimplifies the data.
- The second principal component is an LC that
11
Second Principal Component
- Sometimes a single index still oversimplifies the data.
- The second principal component is an LC that
- Is uncorrelated with the first PC.
- Has the highest variance out of all LCs that satisfy condition 1.
11
Second Principal Component
- Sometimes a single index still oversimplifies the data.
- The second principal component is an LC that
- Is uncorrelated with the first PC.
- Has the highest variance out of all LCs that satisfy condition 1.
- Since there is no need for PC2 to explain any variance already explained by PC1, PC2 and PC1 are uncorrelated.
11
Second Principal Component
- Sometimes a single index still oversimplifies the data.
- The second principal component is an LC that
- Is uncorrelated with the first PC.
- Has the highest variance out of all LCs that satisfy condition 1.
- Since there is no need for PC2 to explain any variance already explained by PC1, PC2 and PC1 are uncorrelated.
- We can plot the first two principal components on a scatter plot.
11
Scatter-plot of PCs
12
The weights
| PC1 | PC2 | |
|---|---|---|
| Income | 0.3473146 | 0.7315324 |
| Illiteracy | -0.4803318 | 0.0693093 |
| LifeExp | 0.4685523 | -0.3243911 |
| Murder | -0.4594049 | 0.4916219 |
| HSGrad | 0.4669687 | 0.3363552 |
- A high (low) weight indicates a strong positive (negative) association between a variable and the corresponding PC.
13
Biplot
- The weight vectors can be plotted on the same scatterplot as the data.
14
Biplot
- The weight vectors can be plotted on the same scatterplot as the data.
- This is called a biplot.
14
Biplot
- The weight vectors can be plotted on the same scatterplot as the data.
- This is called a biplot.
- We can do several useful things with a biplot
14
Biplot
- The weight vectors can be plotted on the same scatterplot as the data.
- This is called a biplot.
- We can do several useful things with a biplot
- See how the observations relate to one another
- See how the variables relate to one another
- See how the observations relate to the variables
14
Types of biplot
- There are multiple ways to draw a biplot.
15
Types of biplot
- There are multiple ways to draw a biplot.
- We will look at two versions
15
Types of biplot
- There are multiple ways to draw a biplot.
- We will look at two versions
- Distance Biplot
- Correlation Biplot
15
Distance Biplot
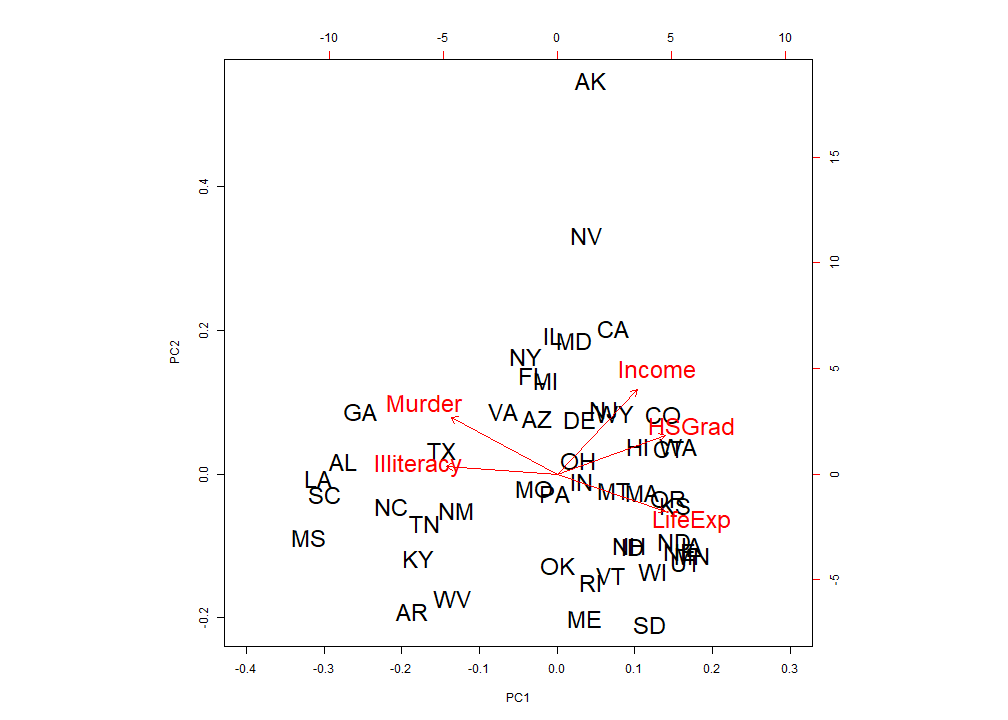
16
Distance Biplot
- The distance between observations implies similarity between observations
17
Distance Biplot
- The distance between observations implies similarity between observations
- Louisiana (LA) and South Carolina (SC) are close therefore are similar.
- Arkansas (AR) and California (CA) are far apart and therefore different.
17
Distance Biplot
- The distance between observations implies similarity between observations
- Louisiana (LA) and South Carolina (SC) are close therefore are similar.
- Arkansas (AR) and California (CA) are far apart and therefore different.
- If the variables are ignored this is identical to a scatter plot of principal components.
17
Correlation Biplot
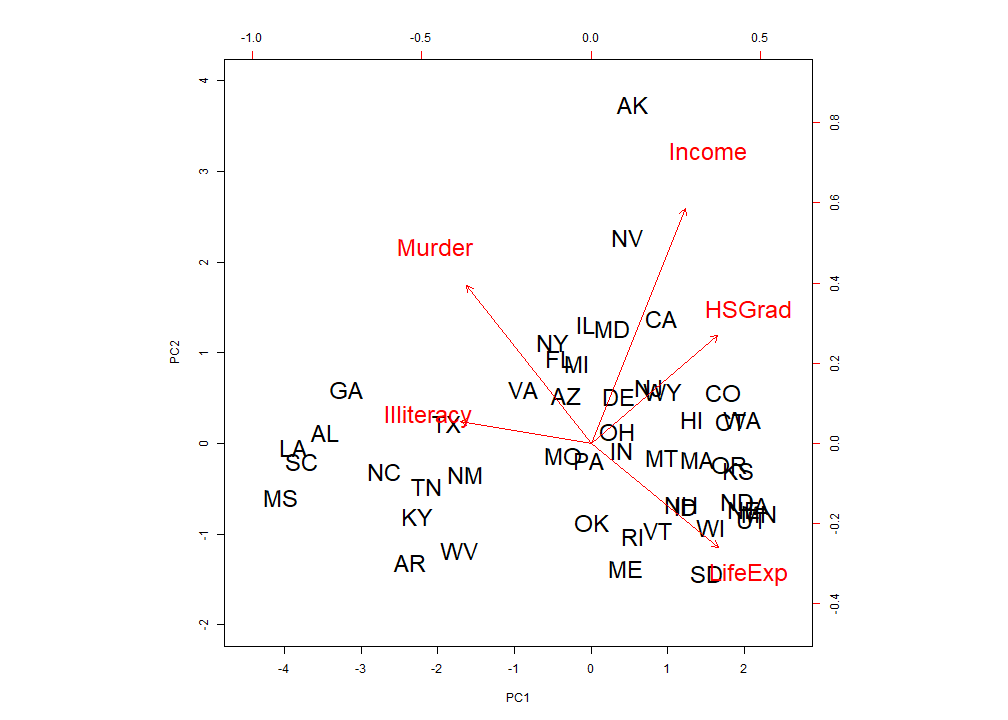
18
Correlations
| Income | Illiteracy | LifeExp | Murder | HSGrad | |
|---|---|---|---|---|---|
| Income | 1.000 | -0.437 | 0.340 | -0.230 | 0.620 |
| Illiteracy | -0.437 | 1.000 | -0.588 | 0.703 | -0.657 |
| LifeExp | 0.340 | -0.588 | 1.000 | -0.781 | 0.582 |
| Murder | -0.230 | 0.703 | -0.781 | 1.000 | -0.488 |
| HSGrad | 0.620 | -0.657 | 0.582 | -0.488 | 1.000 |
19
Correlation Biplot
- The angles between variables tell us something about correlation (approximately)
- Income and HSGrad are highly positively correlated. The angle between them is close to zero.
- LifeExp and Income are close to uncorrelated. The angle between them is close 90 degrees.
- Murder and LifeExp are highly negatively correlated. The angle between them is close 180 degrees.
20
More comparison
- The biplot also allows us to compare observations to variables.
21
More comparison
- The biplot also allows us to compare observations to variables.
- Think of the variables as axes.
21
More comparison
- The biplot also allows us to compare observations to variables.
- Think of the variables as axes.
- Draw the shortest line from each point to the axis.
21
More comparison
- The biplot also allows us to compare observations to variables.
- Think of the variables as axes.
- Draw the shortest line from each point to the axis.
- The position along that axis gives an approximation to the actual value of the variable for that observation.
21
Biplot

22
More PCs
- We can find a third PC, which has the highest variance, while being uncorrelated with PC1 and PC2.
23
More PCs
- We can find a third PC, which has the highest variance, while being uncorrelated with PC1 and PC2.
- We cannot visualise this with a biplot, but there are alternatives depending on the structure of the data.
23
More PCs
- We can find a third PC, which has the highest variance, while being uncorrelated with PC1 and PC2.
- We cannot visualise this with a biplot, but there are alternatives depending on the structure of the data.
- Now a time series example where we consider 3 principal components.
23
A Time Series Example
- The Stock and Watson dataset contains data on 109 macroeconomic variables in the following categories
24
A Time Series Example
- The Stock and Watson dataset contains data on 109
macroeconomic variables in the following categories
- Output
- Prices
- Labour
- Finance
24
A Time Series Example
- The Stock and Watson dataset contains data on 109
macroeconomic variables in the following categories
- Output
- Prices
- Labour
- Finance
- One cannot look at 109 time series plots to visualise general macroeconomic conditions.
24
A Time Series Example
- The Stock and Watson dataset contains data on 109
macroeconomic variables in the following categories
- Output
- Prices
- Labour
- Finance
- One cannot look at 109 time series plots to visualise general macroeconomic conditions.
- However, one can look at time series plots of the principal components of these variables.
24
Plots of PCs
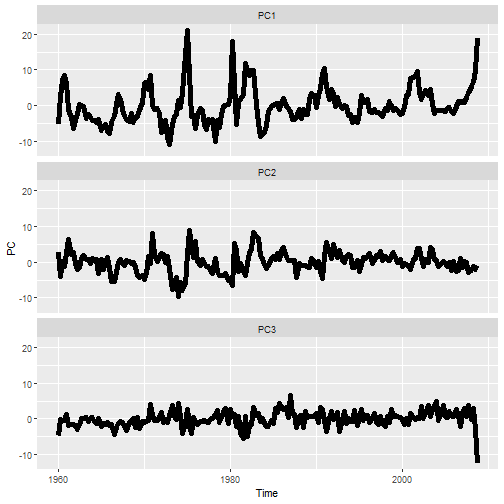
25
All PCs
- There are as many principal components as there are variables.
- Together all p principal components explain all of the variation in all p original variables. p∑j=1Var(Cj)=p∑j=1Var(Yj)
- Where Cj is principal component j and Yj is variable j
26
So why PCs
- However a small number of principal components can often explain a large proportion of the variance
27
So why PCs
- However a small number of principal components can often explain a large proportion of the variance
- In the first example, 2 PCs explain 84% of the total variation of 5 variables.
27
So why PCs
- However a small number of principal components can often explain a large proportion of the variance
- In the first example, 2 PCs explain 84% of the total variation of 5 variables.
- In our second example, 3 PCs explain 35% of the total variation of 109 variables.
27
Summary
- Principal components analysis is useful for
28
Summary
- Principal components analysis is useful for
- Creating a single index
28
Summary
- Principal components analysis is useful for
- Creating a single index
- Seeing how variables are associated with observations on a single biplot.
28
Summary
- Principal components analysis is useful for
- Creating a single index
- Seeing how variables are associated with observations on a single biplot.
- Visualising high-dimensional time series.
28
Summary
- Principal components analysis is useful for
- Creating a single index
- Seeing how variables are associated with observations on a single biplot.
- Visualising high-dimensional time series.
- How do we do it?
28
Implementation of PCA
29
Restriction
- Recall that the objective is to find an LC with a large variance. How could we ‘cheat’ ?
30
Restriction
- Recall that the objective is to find an LC with a large variance. How could we ‘cheat’ ?
- For a single variable Var(wY)=w2Var(Y)
30
Restriction
- Recall that the objective is to find an LC with a large variance. How could we ‘cheat’ ?
- For a single variable Var(wY)=w2Var(Y)
- The variance can be made large by choosing a huge value of w.
30
Restriction
- Recall that the objective is to find an LC with a large variance. How could we ‘cheat’ ?
- For a single variable Var(wY)=w2Var(Y)
- The variance can be made large by choosing a huge value of w.
- For this reason the following restriction (normalization) is used w21+w22…+w2p=1.
30
Standardisation
- A similar logic applies to the units that the variables are measured in.
31
Standardisation
- A similar logic applies to the units that the variables are measured in.
- In the states dataset, income varies from $3000 to $6000, life expectancy varies from 67 years to 73 years.
31
Standardisation
- A similar logic applies to the units that the variables are measured in.
- In the states dataset, income varies from $3000
to $6000, life expectancy varies from 67 years to 73
years.
- Which variable will probably have the larger variance?
31
Standardisation
- A similar logic applies to the units that the variables are measured in.
- In the states dataset, income varies from $3000
to $6000, life expectancy varies from 67 years to 73
years.
- Which variable will probably have the larger variance?
- Income likely to have a larger variance.
31
Different units
- If income is measured in $ ’000s then it will vary from about 3 to 6
32
Different units
- If income is measured in $ ’000s then it will vary from about 3 to 6
- If Life Expectancy in measured in days rather than years it will vary from about 24800 days to 26900 days
32
Different units
- If income is measured in $ ’000s then it will vary from about 3 to 6
- If Life Expectancy in measured in days rather than years
it will vary from about 24800 days to 26900 days
- Which variable will have the larger variance now?
32
Different units
- If income is measured in $ ’000s then it will vary from about 3 to 6
- If Life Expectancy in measured in days rather than years
it will vary from about 24800 days to 26900 days
- Which variable will have the larger variance now?
- The weights can be influenced by the units of measurement.
32
Effect of standardisation
| Std | Unstd | DifUnits | |
|---|---|---|---|
| Income | 0.3473 | 1.0000 | 0.0004 |
| Illiteracy | -0.4803 | -0.0004 | -0.0007 |
| LifeExp | 0.4686 | 0.0007 | 0.9999 |
| Murder | -0.4594 | -0.0014 | -0.0059 |
| HSGrad | 0.4670 | 0.0081 | 0.0096 |
33
Standardise or not?
- While the normalisation w21+w22+…+w2p=1 is always implemented in any software that does PCA, the decision to standardise is up to you.
34
Standardise or not?
- While the normalisation w21+w22+…+w2p=1 is always implemented in any software that does PCA, the decision to standardise is up to you.
- If the variables are measured in the same units then
- No need to standardise.
34
Standardise or not?
- While the normalisation w21+w22+…+w2p=1 is always implemented in any software that does PCA, the decision to standardise is up to you.
- If the variables are measured in the same units then
- No need to standardise.
- If the variables are measured in the different units then
- Standardise the data.
34
Principal Components in R
- There are several functions for doing Principal Components
Analysis in R. We will use
prcomp
35
Principal Components in R
- There are several functions for doing Principal Components
Analysis in R. We will use
prcomp - We can scale in two ways
35
Principal Components in R
- There are several functions for doing Principal Components
Analysis in R. We will use
prcomp - We can scale in two ways
- Scale the data using the function scale
- Include the option
scale.=TRUEwhen calling the functionprcomp
35
Principal Components in R
- There are several functions for doing Principal Components
Analysis in R. We will use
prcomp - We can scale in two ways
- Scale the data using the function scale
- Include the option
scale.=TRUEwhen calling the functionprcomp
- Now we will do PCA on the states dataset using R
35
Principal Components in R
StateSE%>% select_if(is.numeric)%>% #Only use numeric variables prcomp(scale. = TRUE)->pca #Do pca summary(pca) #summary of information## Importance of components:## PC1 PC2 PC3 PC4 PC5## Standard deviation 1.7892 0.9686 0.6317 0.55561 0.39093## Proportion of Variance 0.6403 0.1876 0.0798 0.06174 0.03057## Cumulative Proportion 0.6403 0.8279 0.9077 0.96943 1.0000036
Principal Components in R
- The output of the
prcompfunction is a prcomp object.
37
Principal Components in R
- The output of the
prcompfunction is a prcomp object. - It is a list that contains a lot of information. Of most interest are
37
Principal Components in R
- The output of the
prcompfunction is a prcomp object. - It is a list that contains a lot of information. Of most interest are
- The principal components which are stored in
x - The weights which are stored in
rotation
- The principal components which are stored in
37
Biplot
- The biplot can be produced by:
biplot(pca)- To have the state abbreviations on the plot they need to be attached to the matrix
pca$x
rownames(pca$x)<-pull(StateSE,StateAbb)biplot(pca)- Try it!
38
Correlation biplot
- By default
biplotproduces the distance biplot. - To produce the correlation biplot try
biplot(pca,scale = 0)39
Scree Plot
- Another plot that is easy to create is the Scree plot.
40
Scree Plot
- Another plot that is easy to create is the Scree plot.
- Along the horizontal axis is the Principal Component.
40
Scree Plot
- Another plot that is easy to create is the Scree plot.
- Along the horizontal axis is the Principal Component.
- Along the vertical axis is the variance corresponding to each Principal Component.
40
Scree Plot
- Another plot that is easy to create is the Scree plot.
- Along the horizontal axis is the Principal Component.
- Along the vertical axis is the variance corresponding to each Principal Component.
- The Scree plot indicates how much each PC explains the total variance of the data.
40
Scree Plot
- Another plot that is easy to create is the Scree plot.
- Along the horizontal axis is the Principal Component.
- Along the vertical axis is the variance corresponding to each Principal Component.
- The Scree plot indicates how much each PC explains the total variance of the data.
screeplot(pca,type="lines")40
Scree Plot
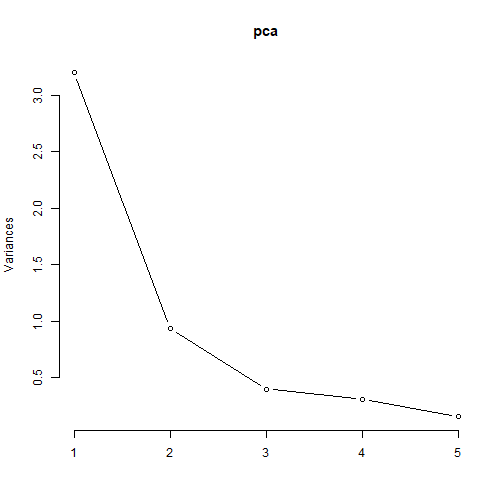
41
Selecting the number of PCs
- The Scree plot can be used to select the number of Principal Components.
42
Selecting the number of PCs
- The Scree plot can be used to select the number of Principal Components.
- Look for a part where the plot flattens out also called the elbow of the Scree Plot.
42
Selecting the number of PCs
- The Scree plot can be used to select the number of Principal Components.
- Look for a part where the plot flattens out also called the elbow of the Scree Plot.
- Another criterion used for standardised data is Kaiser’s Rule. The rule is to select all PCs with a variance greater than 1.
42
Number of PCs
- The way PCs are selected depend on the nature of the analysis.
43
Number of PCs
- The way PCs are selected depend on the nature of the analysis.
- For a visualisation via the biplot, two PCs must be selected.
43
Number of PCs
- The way PCs are selected depend on the nature of the analysis.
- For a visualisation via the biplot, two PCs must be selected.
- In this case check the proportion of variance explained by those PCs
43
Number of PCs
- The way PCs are selected depend on the nature of the analysis.
- For a visualisation via the biplot, two PCs must be selected.
- In this case check the proportion of variance explained by those PCs
- The higher this number the more accurate the biplot
43
PCA and MDS
- When the input distances to MDS are Euclidean MDS and PCA are equivalent.
44
PCA and MDS
- When the input distances to MDS are Euclidean MDS and PCA are equivalent.
- The usual caveat applies that these may only be exactly identical if the MDS solution is rotated.
44
PCA and MDS
- When the input distances to MDS are Euclidean MDS and PCA are equivalent.
- The usual caveat applies that these may only be exactly identical if the MDS solution is rotated.
- The same does not apply generally to PCA. The first PC is defined to maximise variance.
44
Interpreting PCs
- Remember that Principal Components do nothing more than find uncorrelated linear combinations of the variables that explain variance.
45
Interpreting PCs
- Remember that Principal Components do nothing more than find uncorrelated linear combinations of the variables that explain variance.
- Sometimes the nature of the data or analysis from a biplot might imply some sort of interpretation for the PCs.
45
Interpreting PCs
- Remember that Principal Components do nothing more than find uncorrelated linear combinations of the variables that explain variance.
- Sometimes the nature of the data or analysis from a biplot might imply some sort of interpretation for the PCs.
- These interpretations can be subjective so be cautious.
45
Towards Factor Analysis
- For survey data it is often the case that multiple survey questions are measures of the same underlying factor.
46
Towards Factor Analysis
- For survey data it is often the case that multiple survey questions are measures of the same underlying factor.
- For example, at the end of semester you evaluate this unit.
46
Towards Factor Analysis
- For survey data it is often the case that multiple survey questions are measures of the same underlying factor.
- For example, at the end of semester you evaluate this unit.
- Typically you will be asked many questions.
46
Towards Factor Analysis
- For survey data it is often the case that multiple survey questions are measures of the same underlying factor.
- For example, at the end of semester you evaluate this unit.
- Typically you will be asked many questions.
- This is no different from any other customer satisfaction survey
46
Underlying factors
- Although you are asked many questions perhaps there are two underlying factors that drive
47
Underlying factors
- Although you are asked many questions perhaps there are two underlying factors that drive
- The quality of the course materials
- The quality of the teaching staff
47
Underlying factors
- Although you are asked many questions perhaps there are two underlying factors that drive
- The quality of the course materials
- The quality of the teaching staff
- Perhaps the quality of assessment is a third factor.
47
Underlying factors
- Although you are asked many questions perhaps there are two underlying factors that drive
- The quality of the course materials
- The quality of the teaching staff
- Perhaps the quality of assessment is a third factor.
- For survey data, Scree plots and Kaiser's rule can be used to select the number of underlying factors.
47
To do
- These issues will be investigated in the topic on Factor Modelling which has some similarites (but also some important distinctions) when compared to PCA.
48
To do
- These issues will be investigated in the topic on Factor Modelling which has some similarites (but also some important distinctions) when compared to PCA.
- Later on we will also look more deeply into PCA proving some important results.
48
To do
- These issues will be investigated in the topic on Factor Modelling which has some similarites (but also some important distinctions) when compared to PCA.
- Later on we will also look more deeply into PCA proving some important results.
- For now the primary objective is to understand what PCA does and how to implement it in R.
48