Factor Models
High Dimensional Data Analysis
Anastasios Panagiotelis & Ruben Loaiza-Maya
Lecture 8
1
Motivation
2
Boston Housing
- In an earlier tutorial we considered the Boston Housing data.
3
Boston Housing
- In an earlier tutorial we considered the Boston Housing data.
- Each observation is a town (suburb) in the Boston metropolitan area.
3
Boston Housing
- In an earlier tutorial we considered the Boston Housing data.
- Each observation is a town (suburb) in the Boston metropolitan area.
- There are 14 variables measuring demographic information as well as other factors that may influence house price.
3
PCA on Boston Housing
#First load required packageslibrary(tidyverse)Boston<-readRDS('Boston.rds')Boston%>% column_to_rownames('Town')%>% prcomp(scale.=TRUE)->pcaoutscreeplot(pcaout,type = 'l')4
Scree Plot
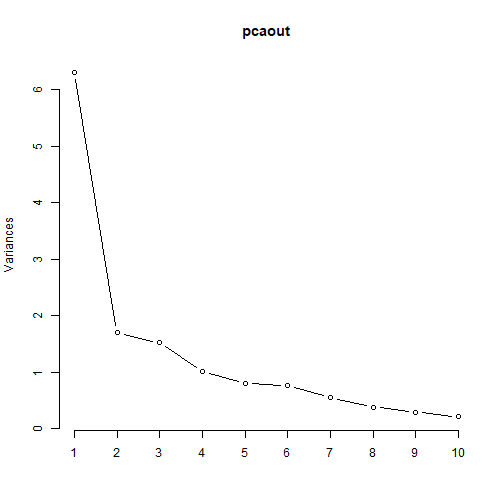
5
Biplot
biplot(pcaout)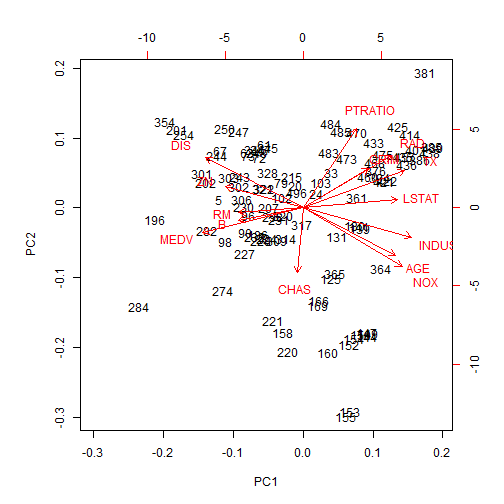
6
Discussion
- Nearly 60% of the variation of all variables in explained by just 2 PCs.
7
Discussion
- Nearly 60% of the variation of all variables in explained by just 2 PCs.
- Can these PCs be interpreted.
7
Discussion
- Nearly 60% of the variation of all variables in explained by just 2 PCs.
- Can these PCs be interpreted.
- Sometimes they can but in this example it is difficult.
7
Discussion
- Nearly 60% of the variation of all variables in explained by just 2 PCs.
- Can these PCs be interpreted.
- Sometimes they can but in this example it is difficult.
- This is not surprising, PCA just finds a linear combination that maximises variances.
7
Discussion
- Nearly 60% of the variation of all variables in explained by just 2 PCs.
- Can these PCs be interpreted.
- Sometimes they can but in this example it is difficult.
- This is not surprising, PCA just finds a linear combination that maximises variances.
- To obtain factors with some interpretation we need a more detailed model.
7
Factor Model
- The factor model is defined as
yij=λj1f1i+λj2f2i+…+ξij
8
Factor Model
- The factor model is defined as
yij=λj1f1i+λj2f2i+…+ξij
- Or in matrix form
yi=Λfi+ξi
- y are observed data, Λ / λ are coefficients, f are latent factors, ξ are error terms.
8
Factor Model
- The factor model is defined as
yij=λj1f1i+λj2f2i+…+ξij
- Or in matrix form
yi=Λfi+ξi
- y are observed data, Λ / λ are coefficients, f are latent factors, ξ are error terms.
- The intercept is left out for simplicity.
8
Notation
- The subscript i denotes the ith cross sectional unit (in the Boston data the town).
9
Notation
- The subscript i denotes the ith cross sectional unit (in the Boston data the town).
- The subscript j denotes the variable (e.g. teacher ratio, distance from downtown etc.)
9
Notation
- The subscript i denotes the ith cross sectional unit (in the Boston data the town).
- The subscript j denotes the variable (e.g. teacher ratio, distance from downtown etc.)
- The dimensions of yi and ξi are p×1 (or 14×1 in the Boston data).
9
Notation
- The subscript i denotes the ith cross sectional unit (in the Boston data the town).
- The subscript j denotes the variable (e.g. teacher ratio, distance from downtown etc.)
- The dimensions of yi and ξi are p×1 (or 14×1 in the Boston data).
- If there are r factors then fi is r×1 and Λ is p×r.
9
Notation
- The subscript i denotes the ith cross sectional unit (in the Boston data the town).
- The subscript j denotes the variable (e.g. teacher ratio, distance from downtown etc.)
- The dimensions of yi and ξi are p×1 (or 14×1 in the Boston data).
- If there are r factors then fi is r×1 and Λ is p×r.
- Verify that all matrix multiplication is conformable.
9
Regression
- This is similar to a regression model. However
- In a regression model there are x on the right hand side that are observed.
- In a factor model these are replaced with f that are unobserved.
10
Regression
- This is similar to a regression model. However
- In a regression model there are x on the right hand side that are observed.
- In a factor model these are replaced with f that are unobserved.
- How can we estimate this model?
10
Assumptions: Errors
- Each idiosyncratic error has its own variance.
- These variances are called unique variance or uniquenesses
11
Assumptions: Errors
- Each idiosyncratic error has its own variance.
- These variances are called unique variance or uniquenesses
- The idiosyncratic errors are uncorrelated with each other.
- This is a crucial assumption
11
Assumptions: Errors
- Each idiosyncratic error has its own variance.
- These variances are called unique variance or uniquenesses
- The idiosyncratic errors are uncorrelated with each other.
- This is a crucial assumption
- Together these imply that Var-Cov(ξ)=Ψ is diagonal.
11
Assumptions: Factors
- The factor and idiosyncratic errors are uncorrelated.
- This is similar to regression
12
Assumptions: Factors
- The factor and idiosyncratic errors are uncorrelated.
- This is similar to regression
- Each factor has a variance of 1.
- This is harmless since the factor is latent.
12
Assumptions: Factors
- The factor and idiosyncratic errors are uncorrelated.
- This is similar to regression
- Each factor has a variance of 1.
- This is harmless since the factor is latent.
- The factors are uncorrelated with each other
- We relax this assumption later on.
12
Assumptions: Factors
- The factor and idiosyncratic errors are uncorrelated.
- This is similar to regression
- Each factor has a variance of 1.
- This is harmless since the factor is latent.
- The factors are uncorrelated with each other
- We relax this assumption later on.
- These imply that Var-Cov(f)=I.
12
Estimation
- In general these assumptions imply that
E(yy′)=Σ=ΛΛ′+Ψ
- The variance is decomposed into two parts
13
Estimation
- In general these assumptions imply that
E(yy′)=Σ=ΛΛ′+Ψ
- The variance is decomposed into two parts
- Part explained by common factors ΛΛ′ .
- This is often called the communality or common variance.
- Part unexplained by common factors Ψ.
- This is often called the uniqueness or unique variance.
13
Estimation
- It is straightforward to estimate Σ with its sample equivalent S
14
Estimation
- It is straightforward to estimate Σ with its sample equivalent S
- We can then choose values ^Λ and ^Ψ so that ^Λ^Λ′+^Ψ is close to S.
14
Estimation
- It is straightforward to estimate Σ with its sample equivalent S
- We can then choose values ^Λ and ^Ψ so that ^Λ^Λ′+^Ψ is close to S.
- There are many ways to do this
14
Estimation
- It is straightforward to estimate Σ with its sample equivalent S
- We can then choose values ^Λ and ^Ψ so that ^Λ^Λ′+^Ψ is close to S.
- There are many ways to do this
- Maximum likelihood estimation is one of the most popular.
14
Estimation issues
- Using Maximum likelihood estimation does require a distributional assumption about the data.
15
Estimation issues
- Using Maximum likelihood estimation does require a distributional assumption about the data.
- The most common assumption is that the data are normally distributed.
15
Estimation issues
- Using Maximum likelihood estimation does require a distributional assumption about the data.
- The most common assumption is that the data are normally distributed.
- Even when this assumption does not hold the maximum likelihood estimate is still quite robust as long as the data do not differ too much from normality.
15
Number of factors
- There are a number of strategies for selecting factors
- Scree plot
- Kaiser rule
- Hypothesis tests
16
Heywood cases
- In some rare cases the maximum likelihood converges to an estimate where the unique variances are negative.
17
Heywood cases
- In some rare cases the maximum likelihood converges to an estimate where the unique variances are negative.
- These are known as Heywood cases
17
Heywood cases
- In some rare cases the maximum likelihood converges to an estimate where the unique variances are negative.
- These are known as Heywood cases
- Since a variance is cannot be negative this is usually caused by
- Selecting too many factors
- Too small a sample size.
17
Factor Analysis in R
18
Using R
- Many packages in R do factor analysis
19
Using R
- Many packages in R do factor analysis
- We use
factanalfrom thestatspackage
19
Using R
- Many packages in R do factor analysis
- We use
factanalfrom thestatspackage - First step use the following code
#First load required packagesBoston<-readRDS('Boston.rds')Boston%>% column_to_rownames('Town')%>% factanal(factors = 2,scores = 'none', rotation = 'none')->facto19
Output
facto$loadings## ## Loadings:## Factor1 Factor2## CRIM 0.548 ## ZN -0.401 0.455 ## INDUS 0.752 -0.513 ## CHAS -0.120 ## NOX 0.630 -0.628 ## RM -0.280 0.371 ## AGE 0.531 -0.576 ## DIS -0.611 0.573 ## RAD 0.923 0.282 ## TX 0.979 0.103 ## PTRATIO 0.472 0.251 ## B -0.459 ## LSTAT 0.532 -0.384 ## MEDV -0.622 0.297 ## ## Factor1 Factor2## SS loadings 5.071 2.080## Proportion Var 0.362 0.149## Cumulative Var 0.362 0.51120
Output
- An advantage of printing the loadings like this is that values close to zero are surpressed.
21
Output
- An advantage of printing the loadings like this is that values close to zero are surpressed.
- This will help with the interpretation of factors.
21
Output
- An advantage of printing the loadings like this is that values close to zero are surpressed.
- This will help with the interpretation of factors.
- For 2 factors, it can be useful to also plot the factors.
21
Output
- An advantage of printing the loadings like this is that values close to zero are surpressed.
- This will help with the interpretation of factors.
- For 2 factors, it can be useful to also plot the factors.
- To prepare the data use the
tidyfunction in thebroompackage.
21
Loadings
library(broom)fa_df<-tidy(facto) #Get into data frame| variable | uniqueness | fl1 | fl2 |
|---|---|---|---|
| CRIM | 0.6957467 | 0.5475829 | 0.0660978 |
| ZN | 0.6318782 | -0.4009173 | 0.4554129 |
| INDUS | 0.1721753 | 0.7517319 | -0.5125564 |
| CHAS | 0.9847352 | -0.0248617 | -0.1202525 |
| NOX | 0.2081610 | 0.6302070 | -0.6282309 |
| RM | 0.7835958 | -0.2803734 | 0.3712276 |
| AGE | 0.3870295 | 0.5306744 | -0.5756284 |
| DIS | 0.2983700 | -0.6109165 | 0.5730549 |
| RAD | 0.0687967 | 0.9228758 | 0.2819623 |
| TX | 0.0307162 | 0.9790952 | 0.1032290 |
| PTRATIO | 0.7146628 | 0.4716189 | 0.2509158 |
| B | 0.7799470 | -0.4585974 | 0.0985286 |
| LSTAT | 0.5691174 | 0.5324934 | -0.3838319 |
| MEDV | 0.5247087 | -0.6220804 | 0.2970937 |
22
Plotting
The plot is clearer if arrows are used
ggplot(fa_df,aes(x=fl1,y=fl2, label=variable))+ geom_segment(aes(xend=fl1, yend=fl2,x=0,y=0), arrow = arrow())+ geom_text(color='red',nudge_y = -0.05)23
Plotting
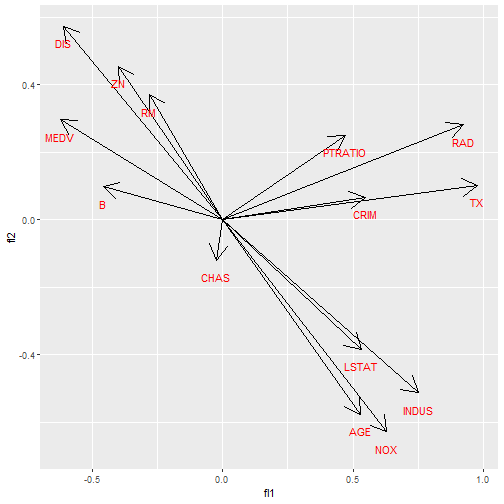
24
Interpretation
It is difficult to interpret these Factors
- Factor 1 seems to take everything into account except the Charles river dummy.
25
Interpretation
It is difficult to interpret these Factors
- Factor 1 seems to take everything into account except the Charles river dummy.
- Factor 2 takes everything into account except crime and race.
25
Interpretation
It is difficult to interpret these Factors
- Factor 1 seems to take everything into account except the Charles river dummy.
- Factor 2 takes everything into account except crime and race.
- It would be easier to interpret the factors if Factor 1 loaded onto a small set of variables and Factor 2 loaded onto a different small set of variables.
25
Interpretation
It is difficult to interpret these Factors
- Factor 1 seems to take everything into account except the Charles river dummy.
- Factor 2 takes everything into account except crime and race.
- It would be easier to interpret the factors if Factor 1 loaded onto a small set of variables and Factor 2 loaded onto a different small set of variables.
- Can we do this?
25
Rotations
Recall the model is
yi=Λfi+ξi
Assume there is an r × r rotation matrix R. Since R′R=I the model above is equivalent to
yi=ΛR′Rfi+ξi
26
The rotation trick
Grouping parts together we have
yi=(ΛR′)(Rfi)+ξi
Now we have new loadings ~Λ=ΛR′ and new factors ~fi=Rfi
- All rotated versions of the loadings and factors explain the data equally well and satisfy all assumptions of the model.
27
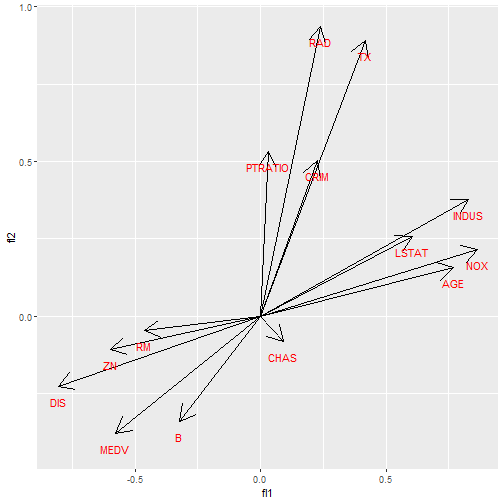
Varimax
- Some rotated versions of the factors may be easier to interpret.
28
Varimax
- Some rotated versions of the factors may be easier to interpret.
- Generally if there are many zero loadings, then the factors are easy to interpret.
28
Varimax
- Some rotated versions of the factors may be easier to interpret.
- Generally if there are many zero loadings, then the factors are easy to interpret.
- An algorithm known as varimax tries to find a rotation with as many loadings close to zero as possible.
28
Varimax
- Some rotated versions of the factors may be easier to interpret.
- Generally if there are many zero loadings, then the factors are easy to interpret.
- An algorithm known as varimax tries to find a rotation with as many loadings close to zero as possible.
- It can be implemented using the
rotation='varimax'option infactanal.
28
Varimax in R
Boston%>% column_to_rownames('Town')%>% factanal(factors = 2,scores = 'none', rotation = 'varimax')->facto_vari29
Loadings
| variable | uniqueness | fl1 | fl2 |
|---|---|---|---|
| CRIM | 0.6957467 | 0.2269179 | 0.5027168 |
| ZN | 0.6318782 | -0.5971858 | -0.1072602 |
| INDUS | 0.1721753 | 0.8276842 | 0.3778276 |
| CHAS | 0.9847352 | 0.0900150 | -0.0835228 |
| NOX | 0.2081610 | 0.8637425 | 0.2139719 |
| RM | 0.7835958 | -0.4627562 | -0.0477061 |
| AGE | 0.3870295 | 0.7672114 | 0.1560450 |
| DIS | 0.2983700 | -0.8065489 | -0.2260306 |
| RAD | 0.0687967 | 0.2365087 | 0.9355566 |
| TX | 0.0307162 | 0.4185322 | 0.8911309 |
| PTRATIO | 0.7146628 | 0.0294672 | 0.5333993 |
| B | 0.7799470 | -0.3217031 | -0.3413600 |
| LSTAT | 0.5691174 | 0.6040563 | 0.2568894 |
| MEDV | 0.5247087 | -0.5762219 | -0.3784402 |
30
Varimax
31
Oblique Rotation
- An orthogonal rotation did not work so instead of considering a matrix where RR=I, consider a matrix GG−1=I yi=ΛGG−1fi+ξi
32
Oblique Rotation
- An orthogonal rotation did not work so instead of considering a matrix where RR=I, consider a matrix GG−1=I yi=ΛGG−1fi+ξi
- Now we have new loadings ~Λ=ΛG and new factors ~fi=G−1fi
32
Oblique Rotation
- An orthogonal rotation did not work so instead of considering a matrix where RR=I, consider a matrix GG−1=I yi=ΛGG−1fi+ξi
- Now we have new loadings ~Λ=ΛG and new factors ~fi=G−1fi
- By setting
rotation='promax'infactanal, an oblique 'rotation' can be carried out.
32
Varimax in R
Boston%>% column_to_rownames('Town')%>% factanal(factors = 2,scores = 'none', rotation = 'promax')->facto_promax33
Loadings
| variable | uniqueness | fl1 | fl2 |
|---|---|---|---|
| CRIM | 0.6957467 | 0.0831127 | 0.5012340 |
| ZN | 0.6318782 | -0.6473132 | 0.0800125 |
| INDUS | 0.1721753 | 0.8163722 | 0.1528374 |
| CHAS | 0.9847352 | 0.1327142 | -0.1267869 |
| NOX | 0.2081610 | 0.9155035 | -0.0480169 |
| RM | 0.7835958 | -0.5140824 | 0.1027513 |
| AGE | 0.3870295 | 0.8251783 | -0.0817944 |
| DIS | 0.2983700 | -0.8456368 | 0.0146546 |
| RAD | 0.0687967 | -0.0584710 | 0.9960908 |
| TX | 0.0307162 | 0.1660177 | 0.8829523 |
| PTRATIO | 0.7146628 | -0.1542302 | 0.6038121 |
| B | 0.7799470 | -0.2487379 | -0.2832482 |
| LSTAT | 0.5691174 | 0.6024474 | 0.0898444 |
| MEDV | 0.5247087 | -0.5276646 | -0.2392111 |
34
Promax

35
Possible Interpretation
- Factor 1 is
- Positively correlated with age.
- Negatively correlated with distance.
- Factor 1 is a geographic factor.
36
Possible Interpretation
- Factor 1 is
- Positively correlated with age.
- Negatively correlated with distance.
- Factor 1 is a geographic factor.
- Factor 2 is
- Positively correlated with crime, pupil-teacher ratio.
- Negatively correlated with the race variable.
- Factor 2 is a socioeconomic factor.
36
More than 2 factors
- If there are more than 2 factors look at the loadings matrix.
37
More than 2 factors
- If there are more than 2 factors look at the loadings matrix.
- The pattern of zeros should give some clue to the interpretation of the factors.
37
More than 2 factors
- If there are more than 2 factors look at the loadings matrix.
- The pattern of zeros should give some clue to the interpretation of the factors.
- Also look for large loadings (in absolute value)
37
Oblique rotation
- Oblique rotations will lead to factors that are correlated with one another.
38
Oblique rotation
- Oblique rotations will lead to factors that are correlated with one another.
- This is not the case for orthogonal factors.
38
Oblique rotation
- Oblique rotations will lead to factors that are correlated with one another.
- This is not the case for orthogonal factors.
- Other rotation options are available by downloading the
package
GPArotation
38
Oblique rotation
- Oblique rotations will lead to factors that are correlated with one another.
- This is not the case for orthogonal factors.
- Other rotation options are available by downloading the
package
GPArotation - Orthogonal Rotations: Varimax, Quartimax, Equimax
38
Oblique rotation
- Oblique rotations will lead to factors that are correlated with one another.
- This is not the case for orthogonal factors.
- Other rotation options are available by downloading the
package
GPArotation - Orthogonal Rotations: Varimax, Quartimax, Equimax
- Oblique Rotations: Promax, Oblimin, Quartimin, Simplimax
38
Factor scores
- The factor scores themselves can be estimated using a variety
of methods. Two are available as options in the factanal
function.
- Regression Scores
- Bartlett’s Scores
- Bartlett’s scores are unbiased estimates
- These can be implemented setting
scores='regression'orscores='Bartlett'infactanal.
39
Estimation alternatives
Other estimation methods can also be used for the factor model.
- One example is Principal Axis Factoring, which is available for
R using the
psychpackage. - Principal Axis Factoring does not require the normality assumption and can be adapted for item response data such as Likert scales.
40
Extended topics
- What we have discussed today is often called exploratory factor analysis.
41
Extended topics
- What we have discussed today is often called exploratory factor analysis.
- In many social sciences the latent variables may themselves influence other observed variables.
41
Extended topics
- What we have discussed today is often called exploratory factor analysis.
- In many social sciences the latent variables may themselves influence other observed variables.
- Such models are called structural equation models.
41
Extended topics
- What we have discussed today is often called exploratory factor analysis.
- In many social sciences the latent variables may themselves influence other observed variables.
- Such models are called structural equation models.
- They can also be estimated by maximum likelihood.
41