Why vectors and matrices?

• Nearly all the methods we cover involve vectors and matrices.
• The earlier lecture on matrices may have felt like it involved remembering many seemingly arbitrary rules.
• The aim of this lecture is to understand the geometric interpretation of vectors which is crucial in making the connection between data, data analysis and visualisation.
• Matrices are important to gain a deep understanding about dimension reduction.

Vectors

• We will think of a 2-dimensional vector in one of three ways:
  • A point in 2-dimensional space
  • An arrow pointing to that point in 2-dimensional space
  • An array of 2 numbers
• All of these ideas work for n-dimensional vectors where n can be 3,4 or any number
• By convention all vectors in this lecture are column vectors.

Vectors as points

Vectors as points

Vectors as arrows

Vectors as arrows

Vectors as numbers

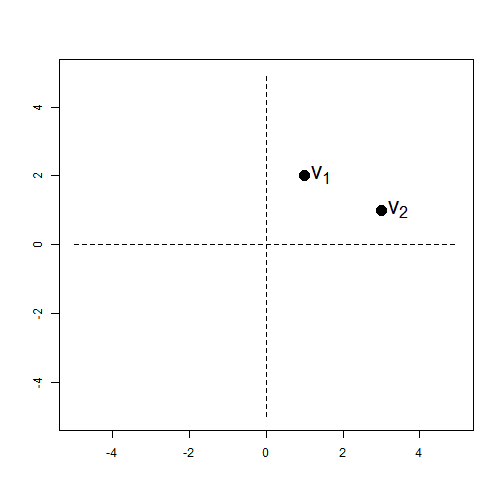
In general a vector is:

$$v=\left[\begin{array}{c}x\\ y\end{array}\right]$$

For our two examples.

$$v_1=\left[\begin{array}{c}1\\ 2\end{array}\right]\text{and}{v}_2=\left[\begin{array}{c}3\\ 1\end{array}\right]$$

Data as a vector

• Consider two examples:
  • The vector $v$ corresponds to a cage where $x$ measures the number of chickens and $y$ measures the number of rabbits.
  • The vector $v$ corresponds to a country where $x$ measures the trade deficit in 2016 and $y$ measures trade deficit in 2017.
• Notice that if we have many cages or countries and plot each of these vectors as points we get a scatterplot

Vectors as points

Vector Operations

• There are two fundamental operations that we can do with vectors
  • Vector addition
  • Scalar multiplication
• We will look at each of these:
  • Geometrically (with pictures) and
  • Algebraically (with numbers)

Vector Addition

The other way

Vector Addition: Geometry

• The operation of adding two vectors is simply to slide one along the other.
• This is called translation
• The order of adding vectors does not matter $v_1+v_2=v_2+v_1$
• This property is called commutativity

With lots of points

Vector Additions: Numbers

Vector addition is as simple as adding up the corresponding numbers

$$\left[\begin{array}{c}1\\ 2\end{array}\right]+\left[\begin{array}{c}3\\ 1\end{array}\right]=\left[\begin{array}{c}1+3\\ 2+1\end{array}\right]=\left[\begin{array}{c}4\\ 3\end{array}\right]$$

Vector Additions: Numbers

Vector addition is as simple as adding up the corresponding numbers

$$\left[\begin{array}{c}1\\ 2\end{array}\right]+\left[\begin{array}{c}3\\ 1\end{array}\right]=\left[\begin{array}{c}1+3\\ 2+1\end{array}\right]=\left[\begin{array}{c}4\\ 3\end{array}\right]$$

Vector Additions: Numbers

Vector addition is as simple as adding up the corresponding numbers

$$\left[\begin{array}{c}1\\ 2\end{array}\right]+\left[\begin{array}{c}3\\ 1\end{array}\right]=\left[\begin{array}{c}1+3\\ 2+1\end{array}\right]=\left[\begin{array}{c}4\\ 3\end{array}\right]$$

Vector Additions: Numbers

Vector addition is as simple as adding up the corresponding numbers

$$\left[\begin{array}{c}1\\ 2\end{array}\right]+\left[\begin{array}{c}3\\ 1\end{array}\right]=\left[\begin{array}{c}1+3\\ 2+1\end{array}\right]=\left[\begin{array}{c}4\\ 3\end{array}\right]$$

Vector Addition and Data

• Vector addition can be meaningful for data.
• If I add a cage with 1 chicken and 3 rabbits to another cage with 2 chickens and 1 rabbits what do I get?
  • A cage with 3 chickens and 4 rabbits.

Vector Addition and Data

• Suppose Australia had a trade deficit of $US1bn in 2016 and $US3bn in 2017 and New Zealand had a trade deficit of $US2bn in 2016 and $US1bn in 2017.
• Australia and New Zealand merge to form a currency union and the trade deficit statistics need to be updated.
  • The new currency union had a trade deficit of $US3bn in 2016 and $US4bn in 2017.

Scalar multiplication

• If we add a number $c$ times we call that multiplication
• We do something similar with vectors.
• If we add a vector to itself $c$ times this is called scalar multiplication.
• We are multiplying a vector by a single number and NOT by another vector.
• This is very different from matrix multiplication.

Scalar multiply by 2

Scalar multiply by 0.5

Scalar multiplication by 2

Scalar multiplication by 0.5

Scalar multiplication by 2

$$\begin{array}{cc}2v_1& =2\left[\begin{array}{c}1\\ 2\end{array}\right]\\ & =\left[\begin{array}{c}2\times 1\\ 2\times 2\end{array}\right]\\ & =\left[\begin{array}{c}2\\ 4\end{array}\right]\end{array}$$

Scalar multiplication by 0.5

$$\begin{array}{cc}0.5v_2& =0.5\left[\begin{array}{c}3\\ 1\end{array}\right]\\ & =\left[\begin{array}{c}0.5\times 3\\ 0.5\times 1\end{array}\right]\\ & =\left[\begin{array}{c}1.5\\ 0.5\end{array}\right]\end{array}$$

Scalar multiplication and data

• How might scalar multiplication be relevant to data?
• Suppose trade deficit is measured in Chinese Yuan instead of $US where 6 Yuan = $US1.
• Then we can get the trade defcit in Yuan by multiplying by the scalar 6.
• Suppose Australia had a trade deficit of $US1bn in 2016 and $US3bn in 2017.
  • This is equivalent to a trade deficit of 6bn Yuan in 2016 and 18bn Yuan in 2017.

Basis vector

• Every vector can be created using
  • Scalar multiplication
  • Vector addition
  • Two basis vectors
• The basis vectors we use are:

$$b_1=\left[\begin{array}{c}1\\ 0\end{array}\right]\text{and}{b}_2=\left[\begin{array}{c}0\\ 1\end{array}\right]$$

How the basis works

• Suppose we want the vector $\left[\begin{array}{c}x\\ y\end{array}\right]$
• This is given by

$$x{b}_1+y{b}_2$$ or $$x\left[\begin{array}{c}1\\ 0\end{array}\right]+y\left[\begin{array}{c}0\\ 1\end{array}\right]$$

Build a vector

Matrices

• You have learnt about matrices before as an array of numbers.
• Today think about matrices as transforming points in space.
• By multiplying a vector by a matrix, points in space are stetched, rotated and flipped around
• But what does this have to do with an array of numbers?

Example of a matrix

• Consider the following matrix $$M=\left[\begin{array}{cc}5& 1\\ 2& 4\end{array}\right]$$
• Think of this as something that moves all the points in space to a new address.
• It encodes where $b_1$ and $b_2$ get moved to.

Change of basis

Multiplying by the matrix $M=\left[\begin{array}{cc}5& 1\\ 2& 4\end{array}\right]$ will:

Move the vector $b_1=\left[\begin{array}{c}1\\ 0\end{array}\right]$ to $b_1^{\ast }=\left[\begin{array}{c}5\\ 2\end{array}\right]$

Move the vector $b_2=\left[\begin{array}{c}0\\ 1\end{array}\right]$ to $b_2^{\ast }=\left[\begin{array}{c}1\\ 4\end{array}\right]$

Matrix multiplication is a very different type of multiplication than scalar multiplication.

Change of basis

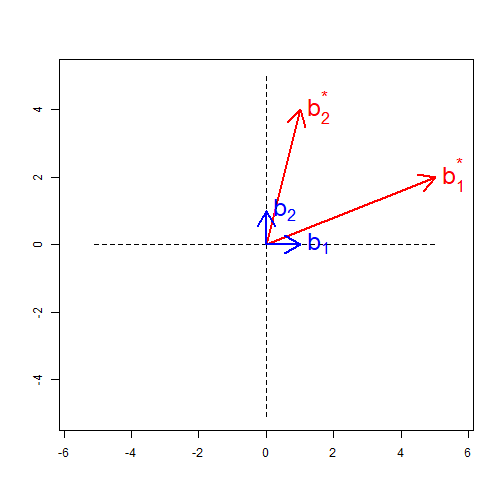
Old Basis

$$\begin{array}{cc}v& =x{b}_1+y{b}_2\\ & =x\left[\begin{array}{c}1\\ 0\end{array}\right]+y\left[\begin{array}{c}0\\ 1\end{array}\right]\\ & =\left[\begin{array}{c}x\\ y\end{array}\right]\end{array}$$

New Basis

$$\begin{array}{cc}{v}^{\ast }& =x{b}_1^{\ast }+y{b}_2^{\ast }\\ & =x\left[\begin{array}{c}5\\ 2\end{array}\right]+y\left[\begin{array}{c}1\\ 4\end{array}\right]\\ & =\left[\begin{array}{c}5x+y\\ 2x+4y\end{array}\right]\end{array}$$

In general

Multiplying by the matrix $M$ moves all vectors $v$ to $v^{\ast }$

We can write this as:

$$v^{\ast }=Mv=\left[\begin{array}{cc}5& 1\\ 2& 4\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}5x+y\\ 2x+4y\end{array}\right]$$

Another way to think of it is as multiplying the rows of $M$ by the column $v$

Matrix Multiplication in General

Matrix Multiplication and Data

An simple application of matrix multiplication is to create new variables.

• Suppose we want a matrix to transform :
  • The number of chickens and number of rabbits to...
  • The number of heads and the number of feet.

Answer

• First basis vector is the number of heads and feet of each chicken.
• Second basis vector is the number of heads and feet of each rabbit.

$$\left[\begin{array}{cc}1& 1\\ 2& 4\end{array}\right]$$

Another one

• Suppose we want a matrix to transform:
  • The trade deficit in 2016 and trade deficit in 2017 to...
  • The average trade deficit from 2016 to 2017 and the change in the trade deficit between 2016 and 2017

What does this matrix look like? Try yourselves.

Answer

• First basis vector average and change if trade deficit was $1 in 2016 and $0 in 2017.
• Second basis vector average and change if trade deficit was $0 in 2016 and $1 in 2017.

$$\left[\begin{array}{cc}0.5& 0.5\\ -1& 1\end{array}\right]$$

Non-Square Matrices

• So far we have only considered $2\times 2$ matrices.
• These move every point in 2D space to another point in 2D space
• However we can have a matrix with 3 rows and 2 columns (or $3\times 2$ matrix).

$$M=\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]$$

Non-square Matrices

$$\begin{array}{cc}Mz& =\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]\\ & =x\left[\begin{array}{c}1\\ 3\\ 5\end{array}\right]+y\left[\begin{array}{c}2\\ 4\\ 6\end{array}\right]\\ & =\left[\begin{array}{c}x+2y\\ 3x+4y\\ 5x+6y\end{array}\right]\end{array}$$

Non-square matrices

• Matrix multiplication works in the same way
• However the input is a 2-dimensional vector but the output is a 3-dimensional vector
• Multiplying by a non-square matrix changes the dimension
• The points will still lie in a two-dimensional subspace of three-dimensional space.

In factor analysis

• For an example of this consider the factor model and in particular the component $\Lambda f_i$.
• This takes a low-dimensional set of factors and maps them to a high-dimensional vector of data.
• What about multiplying by a $2\times 3$ matrix?

Dimension reduction

• Multiplying by a $2\times 3$ matrix takes a $3$-dimensional vector and maps it to a point in $2$-dimensional space.
• This is an example of dimension reduction
• For instance taking the first two principal component of data is the same as multiplying the data by a $2\times p$ matrix

Matrix composition

• What does it mean to multiply matrices?
• What does $FG$ when $G$ is a $4\times 2$ matrix and $F$ a $3\times 4$ matrix?
• It is as a composition of transformations:
  • Transform a $2$-dimensional vector $v$ into a $4$-dimensional vector by multiplying by the $4\times 2$ matrix $G$
  • Transorm the result into a $3$-dimensional vector by multiplying by a $3\times 4$ matrix $F$

Mathematically

• When reading below go from right to left:

$$\underset{(3\times 2)}{H}\underleftarrow{\times }\underset{(2\times 1)}{v}\underset{=}{=}\underset{(3\times 4)}{F}\underleftarrow{\times }\underset{(4\times 2)}{G}\underleftarrow{\times }\underset{(2\times 1)}{v}$$

• The matrix $H=FG$ is a composition of doing $G$ and then $F$

Matrix multiplication

• What happens if you try to multiply $GFv$? $$\underset{(4\times 2)}{G}\underset{\nleftarrow }{\times }\underset{(3\times 4)}{F}\underset{\nleftarrow }{\times }\underset{(2\times 1)}{v}$$
• Going from right to left, $F$ will try to transform a 4-dimensional vector to a 3-dimensional vector and cannot take the is a 2-dimensional vector $v$ as its input!
• Also $G$ transforms a 2-dimensional vector to a 4-dimensional vector so cannot take the 3-dimensional output of $F$ as its input.

Matrix Multiplication

• Although it is possible to get $FG$ it is impossible to get $GF$.
• In general, for matrix multiplication $AB\ne BA$ even for square matrices.
• Matrix multiplication is non-commutative.

Inner product

• One final operation with vectors is called the inner product.
• The inner product of two vectors $x$ and $y$ is defined as $x^{\prime }y$.
• The inner product of a vector with itself $x^{\prime }x$ is the length of the vector squared.

Orthogonality

• An interesting case is when the inner product between two vectors is zero.
  • $x^{\prime }y=0$
• In this case, the vectors $x$ and $y$ are at a 90 degree angle to one another.
• This is also called orthogonality.

Rotation matrix

• Another important matrix is known as a orthogonal rotation matrix.
• It spins all the points around keeping them the same distance from the origin and from each other.
• The word orthogonal means that the new basis vectors are at right angles to one another.

Rotation Matrix

• In matrix algebra rotation can be defined in any dimension.
• It is easiest to understand in two dimensions.
• An example of a rotation matrix in two dimensions is: $$R=\left[\begin{array}{cc}0.8& -0.6\\ 0.6& 0.8\end{array}\right]$$

Rotation Matrix

Rotation matrix

• The new basis vectors should have a length of 1 therefore $r_i^{\prime }{r}_i=1$ where $r_i$ are the columns of $R$.
• The new basis vectors should be at right angles $r_i^{\prime }{r}_j=0$
• A rotation matrix $R$ has the property $R^{\prime }R=I$

Rotations in PCA

• In PCA the weights of the principal components have two properties
  • $w_i^{\prime }{w}_i=1$
  • $w_i^{\prime }{w}_j=0$
• All $p$ principal components can be obtained by multiplying by a rotation matrix by $p$-dimensional data.
• Taking principal components rotates the data.

Rotations in Factor Analysis

• In factor analysis rotation was used to obtain more interpretable factors.
• This was a $r$-dimensional rotation of the factors rather than the data.
• Again this involved multiplying by a rotation matrix.

Conclusion

• Understand the geometry of matrix algebra assists in understanding PCA and Factor analysis in particular.
• PCA forms new variables as linear combinations of old variables.
  • This corresponds to matrix multiplication.
• The role of rotation should now also be understood.
• The next step is to understand the importance of matrix decompositions in the methods covered so far.