Dimension ReductionHigh Dimensional Data AnalysisAnastasios Panagiotelis & Ruben Loaiza-MayaLecture 101

A proof2

How to do PCAOver the next few slides, we will derive how to get the first principal component.
3

How to do PCAOver the next few slides, we will derive how to get the first principal component.
This eventually leads us to the eigenvalue decomposition.
3

How to do PCAOver the next few slides, we will derive how to get the first principal component.
This eventually leads us to the eigenvalue decomposition.
The eigenvalue decomposition and its more general form known as the singular value decomposition are crucial to all dimension reduction techniques.
3

How to do PCAOver the next few slides, we will derive how to get the first principal component.
This eventually leads us to the eigenvalue decomposition.
The eigenvalue decomposition and its more general form known as the singular value decomposition are crucial to all dimension reduction techniques.
This will be challenging.
3

First PCRecall that the principal component is The linear combination of the variables
With maximum variance
Subject to the squared weights summing to 1.

4

Linear CombinationLet ci=w1yi1+…+wpyipci=w1yi1+…+wpyip 
5

Linear CombinationLet ci=w1yi1+…+wpyipci=w1yi1+…+wpyip 
In matrix/vector form ci=w′yici=w′yi 
5

Linear CombinationLet ci=w1yi1+…+wpyipci=w1yi1+…+wpyip 
In matrix/vector form ci=w′yici=w′yi 
What are the dimensions of cici, ww and yiyi?
5

Linear CombinationLet ci=w1yi1+…+wpyipci=w1yi1+…+wpyip 
In matrix/vector form ci=w′yici=w′yi 
What are the dimensions of cici, ww and yiyi?
Both ww and yiyi are p×1p×1 vectors, while cici is a scalar.
5

Variance

The variance of the linear combination is given by

$Var (c) = \frac{\sum_{i = 1}^{n} c_{i}^{2}}{n - 1} = \frac{\sum_{i = 1}^{n} (w^{'} y_{i})^{2}}{n - 1}$

Assumed that all $y$ 's have a mean of zero.
Everything still works without this assumption but is messier.

A trickNote that w1yi1+…+wpyipw1yi1+…+wpyip has been written as  w′yiw′yi, but...
7

A trickNote that w1yi1+…+wpyipw1yi1+…+wpyip has been written as  w′yiw′yi, but...
... it can also be written as y′iwyi′w.
7

A trickNote that w1yi1+…+wpyipw1yi1+…+wpyip has been written as  w′yiw′yi, but...
... it can also be written as y′iwyi′w.
This in turn implies that c2i=w′yiy′iwci2=w′yiyi′w.  Substituting into the variance formula gives.
7

A trickNote that w1yi1+…+wpyipw1yi1+…+wpyip has been written as  w′yiw′yi, but...
... it can also be written as y′iwyi′w.
This in turn implies that c2i=w′yiy′iwci2=w′yiyi′w.  Substituting into the variance formula gives.
Var(c)=n∑i=1c2in−1=n∑i=1w′yiy′iwn−1Var(c)=∑i=1nci2n−1=∑i=1nw′yiyi′wn−1
7

Linearity

Linearity implies that anything without an $i$ subscript can be taken outside the summation sign.

$Var (c) = \frac{\sum_{i = 1}^{n} c_{i}^{2}}{n - 1} = \frac{w^{'} (\sum_{i = 1}^{n} y_{i} y_{i}^{'}) w}{n - 1}$

Scalar multiplication

The order of scalar multiplication does not matter allowing the following

$\begin{aligned} Var (c) & = w^{'} (\frac{\sum_{i = 1}^{n} y_{i} y_{i}^{'}}{n - 1}) w \\ = w^{'} S w \end{aligned}$

Recall $S$ is the variance covariance matrix

Objective

We want to choose $w$ to maximise the variance while ensuring that $w_{1}^{2} + \dots + w_{p}^{2} = w^{'} w = 1$ . We write this as

$\begin{aligned} max_{w} & w^{'} S w \\ s.t. & w^{'} w = 1 \end{aligned}$

Optimisation11

Constrained Optimisation

Solving the constrained optimisation above is equivalent to solving the following unconstrained problem

$max_{w, λ} w^{'} S w - λ (w^{'} w - 1)$

GradientMany optimisation problems involve using the gradient or slope of an objective function.
13

GradientMany optimisation problems involve using the gradient or slope of an objective function.
Think of an analogy of climbing a hill.
13

GradientMany optimisation problems involve using the gradient or slope of an objective function.
Think of an analogy of climbing a hill.
If the gradient is positive then you can go higher by walking forwards.
13

GradientMany optimisation problems involve using the gradient or slope of an objective function.
Think of an analogy of climbing a hill.
If the gradient is positive then you can go higher by walking forwards.
If the gradient is negative then you can go higher by walking backwards.
13

GradientMany optimisation problems involve using the gradient or slope of an objective function.
Think of an analogy of climbing a hill.
If the gradient is positive then you can go higher by walking forwards.
If the gradient is negative then you can go higher by walking backwards.
The top of the hill is where the gradient is zero.
13

GradientTo compute the gradient we need to use matrix calculus.
14

GradientTo compute the gradient we need to use matrix calculus.
What does it mean to differentiate with respect to ww?
14

GradientTo compute the gradient we need to use matrix calculus.
What does it mean to differentiate with respect to ww?
It means we differentiate with respect to w1w1, w2w2, etc
14

GradientTo compute the gradient we need to use matrix calculus.
What does it mean to differentiate with respect to ww?
It means we differentiate with respect to w1w1, w2w2, etc
All up pp first derivatives are found.  These can be stored in a vector.
14

First Order Conditions

Differentiating w.r.t. $w$ gives

$\frac{\partial (w^{'} S w - λ (w^{'} w - 1))}{\partial w} = 2 S w - 2 λ w$

Differentiating w.r.t. $λ$ gives

$\frac{\partial (w^{'} S w - λ (w^{'} w - 1))}{\partial λ} = - (w^{'} w - 1)$

How did we do that?

The key result is that for any square, symmetric matrix $A$ it holds that

$\frac{\partial w^{'} A w}{\partial w} = 2 A w$ This is the matrix version of the rule that the derivative of $\partial a w^{2} / \partial w = 2 a w$ . From this result, the matrix result can be derived (but this is tedious).

Eigenvalue Problem

The gradient will be zero when $2 S w - 2 λ w = 0$ or simplifying when

$S w = λ w$

This is a very famous problem known as the eigenvalue problem. Suppose $\tilde{λ}$ and $\tilde{w}$ provide a solutions then

Eigenvalue Problem

The gradient will be zero when $2 S w - 2 λ w = 0$ or simplifying when

$S w = λ w$

This is a very famous problem known as the eigenvalue problem. Suppose $\tilde{λ}$ and $\tilde{w}$ provide a solutions then

The value of $\tilde{λ}$ is called an eigenvalue
The vector $\tilde{w}$ is called an eigenvector

Eigenvalue ProblemFor 2×22×2, 3×33×3 and 4×44×4 matrices there are formulas for ~λλ~.
18

Eigenvalue ProblemFor 2×22×2, 3×33×3 and 4×44×4 matrices there are formulas for ~λλ~.
These are hideous
18

Eigenvalue ProblemFor 2×22×2, 3×33×3 and 4×44×4 matrices there are formulas for ~λλ~.
These are hideous
For 5×55×5 and beyond there is no formula
18

Eigenvalue ProblemFor 2×22×2, 3×33×3 and 4×44×4 matrices there are formulas for ~λλ~.
These are hideous
For 5×55×5 and beyond there is no formula
A solution is found using numerical methods (i.e. a computer algorithm).
18

Geometric ViewRecall that multiplying by a matrix moves vectors around, changing their length and direction.
19

Geometric ViewRecall that multiplying by a matrix moves vectors around, changing their length and direction.
However for any matrix there will be some vector whose direction does not change, but only the length.
19

Geometric ViewRecall that multiplying by a matrix moves vectors around, changing their length and direction.
However for any matrix there will be some vector whose direction does not change, but only the length.
This vector is an eigenvector.
19

Geometric ViewRecall that multiplying by a matrix moves vectors around, changing their length and direction.
However for any matrix there will be some vector whose direction does not change, but only the length.
This vector is an eigenvector.
The extent to which the length is changed is the eigenvalue.
19

Multiple solutionsIn general there are multiple pairs of (~λ,~w)(λ~,w~) that solve the eigenvalue problem.
20

Multiple solutionsIn general there are multiple pairs of (~λ,~w)(λ~,w~) that solve the eigenvalue problem.
Which one maximises the variance?
20

Multiple solutionsIn general there are multiple pairs of (~λ,~w)(λ~,w~) that solve the eigenvalue problem.
Which one maximises the variance?
Let ~ww~ be an eigenvector and its associated eigenvalue be ~λλ~.
20

Multiple solutionsIn general there are multiple pairs of (~λ,~w)(λ~,w~) that solve the eigenvalue problem.
Which one maximises the variance?
Let ~ww~ be an eigenvector and its associated eigenvalue be ~λλ~.
What is the variance of the linear combination ~w′yw~′y?
20

Answer

We have already shown that the variance will be ${\tilde{w}}^{'} S \tilde{w}$ . Since $\tilde{w}$ is an eigenvector it must hold that

$S \tilde{w} = \tilde{λ} \tilde{w}$

Answer

We have already shown that the variance will be ${\tilde{w}}^{'} S \tilde{w}$ . Since $\tilde{w}$ is an eigenvector it must hold that

$S \tilde{w} = \tilde{λ} \tilde{w}$ which implies

$\begin{aligned} {\tilde{w}}^{'} S \tilde{w} & = {\tilde{w}}^{'} \tilde{λ} \tilde{w} \\ = \tilde{λ} {\tilde{w}}^{'} \tilde{w} \end{aligned}$

VarianceSince ~w′~w=1w~′w~=1 this implies that the variance of the linear combination is ~λλ~.
22

VarianceSince ~w′~w=1w~′w~=1 this implies that the variance of the linear combination is ~λλ~.
The weights for the first principal component is given by the eigenvector that corresponds to the largest eigenvalue. 
22

VarianceSince ~w′~w=1w~′w~=1 this implies that the variance of the linear combination is ~λλ~.
The weights for the first principal component is given by the eigenvector that corresponds to the largest eigenvalue. 
The weights of the remaining principal components are given by the other eigenvectors.
22

Matrix Decompositions23

Spectral Theorem

Since $S$ is a symmetric matrix it can decomposed as

$\underset{(p \times p)}{S} = \underset{(p \times p)}{W} \underset{(p \times p)}{Λ} {\underset{(p \times p)}{W}}^{'}$

Spectral Theorem

Since $S$ is a symmetric matrix it can decomposed as

$\underset{(p \times p)}{S} = \underset{(p \times p)}{W} \underset{(p \times p)}{Λ} {\underset{(p \times p)}{W}}^{'}$

The columns of $W$ are eigenvectors of $S$

Spectral Theorem

Since $S$ is a symmetric matrix it can decomposed as

$\underset{(p \times p)}{S} = \underset{(p \times p)}{W} \underset{(p \times p)}{Λ} {\underset{(p \times p)}{W}}^{'}$

The columns of $W$ are eigenvectors of $S$
$Λ$ is a matrix with the eigenvalues along the main diagonal and zeros on the off diagonal.

Spectral Theorem

Since $S$ is a symmetric matrix it can decomposed as

$\underset{(p \times p)}{S} = \underset{(p \times p)}{W} \underset{(p \times p)}{Λ} {\underset{(p \times p)}{W}}^{'}$

The columns of $W$ are eigenvectors of $S$
$Λ$ is a matrix with the eigenvalues along the main diagonal and zeros on the off diagonal.
The eigenvalues and eigenvectors can be rearranged so by convention eigenvalues in $Λ$ are sorted from largest to smallest.

RotationThe full vector of principal components for observation ii is given by ci=W′yici=W′yi
25

RotationThe full vector of principal components for observation ii is given by ci=W′yici=W′yi
The eigenvectors of a symmetric matrix are also orthogonal (A proof of why this is true can be provided for anyone who is curious).
25

RotationThe full vector of principal components for observation ii is given by ci=W′yici=W′yi
The eigenvectors of a symmetric matrix are also orthogonal (A proof of why this is true can be provided for anyone who is curious).
Orthogonality implies that the matrix of eigenvectors WW is a rotation matrix.
25

RotationThe full vector of principal components for observation ii is given by ci=W′yici=W′yi
The eigenvectors of a symmetric matrix are also orthogonal (A proof of why this is true can be provided for anyone who is curious).
Orthogonality implies that the matrix of eigenvectors WW is a rotation matrix.
For this reason we consider PCA to be a rotation of the data.
25

PCA as an approximation

It can be shown that an equivalent way of writing the eigenvalue decomposition is

$\begin{aligned} \underset{(p \times p)}{S} & = \underset{(p \times p)}{W} \underset{(p \times p)}{Λ} {\underset{(p \times p)}{W}}^{'} \\ = \sum_{j = 1}^{p} \underset{(1 \times 1)}{λ_{j}} \underset{(p \times 1)}{w_{j}} \underset{(1 \times p)}{w_{j}^{'}} \end{aligned}$

PCA as an approximation

If some eigenvalues are small they can be ignored.

$\begin{aligned} S & = \sum_{j = 1}^{p} λ_{j} w_{j} w_{j}^{'} \\ \approx \sum_{j = 1}^{r} λ_{j} w_{j} w_{j}^{'} \end{aligned}$

Only $r << p$ eigenvalues are used.

DecompositionConsider a 50×5050×50 covariance matrix.
28

DecompositionConsider a 50×5050×50 covariance matrix.
There are 1275 variances and covariances to estimate
28

DecompositionConsider a 50×5050×50 covariance matrix.
There are 1275 variances and covariances to estimate
Suppose the data can be summarised by just 5 factors/principal components.
28

DecompositionConsider a 50×5050×50 covariance matrix.
There are 1275 variances and covariances to estimate
Suppose the data can be summarised by just 5 factors/principal components.
Then the matrix can be approximated with just 5 eigenvalues and eigenvectors (255 numbers).
28

In General

For matrix $X$ that is possibly non-symmetric and possibly non-square a similar decomposition known as the singular value decomposition can be used.

$\underset{(n \times p)}{Y} = \underset{(n \times n)}{U} \underset{(n \times p)}{D} \underset{(p \times p)}{V^{'}}$

The matrices $U$ and $V$ are rotations

Structure of DIf n>pn>p
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣d1⋯0⋮⋱⋮0⋯dp0⋯0⋮⋮⋮0⋯0⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦[d1⋯0⋮⋱⋮0⋯dp0⋯0⋮⋮⋮0⋯0]
30

Structure of DIf n<pn<p
⎡⎢
⎢⎣d1⋯00⋯0⋮⋱⋮⋮⋮⋮0⋯dn0⋯0⎤⎥
⎥⎦[d1⋯00⋯0⋮⋱⋮⋮⋮⋮0⋯dn0⋯0]
In both cases all di>0di>0
31

Structure of DIf n<pn<p
⎡⎢
⎢⎣d1⋯00⋯0⋮⋱⋮⋮⋮⋮0⋯dn0⋯0⎤⎥
⎥⎦[d1⋯00⋯0⋮⋱⋮⋮⋮⋮0⋯dn0⋯0]
In both cases all di>0di>0
These are called singular values.
31

Singular Values

The singular values are ordered from largest to smallest allowing for an approximation

$\begin{aligned} Y & = \sum_{j = 1}^{min (n, p)} d_{j} u_{j} v_{j}^{'} \\ \approx \sum_{j = 1}^{r} d_{j} u_{j} v_{j}^{'} \end{aligned}$

for $r << m i n (n, p)$

Biplots and the SVDWhen YY is the data matrix there is a connection between the biplot and the SVD.
33

Biplots and the SVDWhen YY is the data matrix there is a connection between the biplot and the SVD.
For the distance biplot, the first two columns of UDUD are plotted as points and the first two columns of VV as arrows
33

Biplots and the SVDWhen YY is the data matrix there is a connection between the biplot and the SVD.
For the distance biplot, the first two columns of UDUD are plotted as points and the first two columns of VV as arrows
For the correlation biplot plot the first two columns of UU are plotted as points the first two columns of VDVD as arrows
33

Biplots and the SVDWhen YY is the data matrix there is a connection between the biplot and the SVD.
For the distance biplot, the first two columns of UDUD are plotted as points and the first two columns of VV as arrows
For the correlation biplot plot the first two columns of UU are plotted as points the first two columns of VDVD as arrows
In general plot the first two columns of UDκUDκ and the first two columns of VD(1−κ)VD(1−κ)
33

Biplots and the SVDWhen YY is the data matrix there is a connection between the biplot and the SVD.
For the distance biplot, the first two columns of UDUD are plotted as points and the first two columns of VV as arrows
For the correlation biplot plot the first two columns of UU are plotted as points the first two columns of VDVD as arrows
In general plot the first two columns of UDκUDκ and the first two columns of VD(1−κ)VD(1−κ)
In R, κκ is set by the scale option of biplot
33

A final example34

A picture

PixelsFor the computer this picture is a matrix
36

PixelsFor the computer this picture is a matrix
Each pixel on the screen has a number between 0 and 1.
36

PixelsFor the computer this picture is a matrix
Each pixel on the screen has a number between 0 and 1.Numbers closer to 0 display as lighter shades of grey

36

PixelsFor the computer this picture is a matrix
Each pixel on the screen has a number between 0 and 1.Numbers closer to 0 display as lighter shades of grey
Numbers closer to 1 display as darker shades of grey

36

PixelsFor the computer this picture is a matrix
Each pixel on the screen has a number between 0 and 1.Numbers closer to 0 display as lighter shades of grey
Numbers closer to 1 display as darker shades of grey

What if we do the SVD on this matrix?
36

SVDAll up there are 232×218=50576232×218=50576 pixels.
37

SVDAll up there are 232×218=50576232×218=50576 pixels.
Suppose we approximate this matrix with 20 singular values
37

SVDAll up there are 232×218=50576232×218=50576 pixels.
Suppose we approximate this matrix with 20 singular values
Then U(r)U(r) is 232×20=4640232×20=4640
37

SVDAll up there are 232×218=50576232×218=50576 pixels.
Suppose we approximate this matrix with 20 singular values
Then U(r)U(r) is 232×20=4640232×20=4640
Then V(r)V(r) is 218×20=4360218×20=4360
37

SVDAll up there are 232×218=50576232×218=50576 pixels.
Suppose we approximate this matrix with 20 singular values
Then U(r)U(r) is 232×20=4640232×20=4640
Then V(r)V(r) is 218×20=4360218×20=4360
Including the 20 singular values themselves, we summarise 50576 numbers using only 4640+4360+20=90204640+4360+20=9020 numbers.
37

Approximation

DiscussionUsing only 20 singular values we do not lose much information.
39

DiscussionUsing only 20 singular values we do not lose much information.
What if we reconstruct the picture using singular value 21 to singular value 218?
39

DiscussionUsing only 20 singular values we do not lose much information.
What if we reconstruct the picture using singular value 21 to singular value 218?
This uses a lot more information.  Does it give a clearer approximation?
39

Using remaining singular values

Singular values

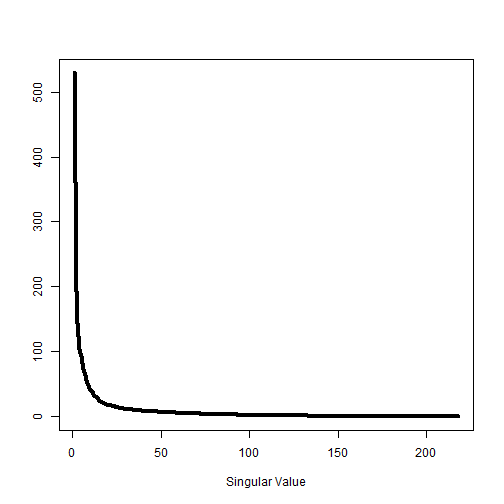
ConclusionThe main idea is that the SVD summarises the important information in the matrix into a small number of singular values.
42

ConclusionThe main idea is that the SVD summarises the important information in the matrix into a small number of singular values.
Rotating so that we can isolate the dimensions associated with those singular values is the geometry behind dimension reduction.
42

ConclusionThe main idea is that the SVD summarises the important information in the matrix into a small number of singular values.
Rotating so that we can isolate the dimensions associated with those singular values is the geometry behind dimension reduction.
This applies to PCA, factor analysis and MDS as well as to compressing images.
42

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help