Correspondence Analysis
High Dimensional Data Analysis
Anastasios Panagiotelis & Ruben Loaiza-Maya
Lecture 11
1
Motivation
2
Non-metric data
- So far we have looked at dimension reduction methods such as PCA and MDS where:
3
Non-metric data
- So far we have looked at dimension reduction methods such as PCA
and MDS where:
- The number of variables is large
3
Non-metric data
- So far we have looked at dimension reduction methods such as PCA
and MDS where:
- The number of variables is large
- The data are (mostly) metric data
3
Non-metric data
- So far we have looked at dimension reduction methods such as PCA
and MDS where:
- The number of variables is large
- The data are (mostly) metric data
- Today we cover tools for understanding the relationships between nominal/categorical data.
3
Non-metric data
- So far we have looked at dimension reduction methods such as PCA
and MDS where:
- The number of variables is large
- The data are (mostly) metric data
- Today we cover tools for understanding the relationships between nominal/categorical data.
- We focus on the case where there are only two variables, but a potentially large number of categories for each variable.
3
Outline
- First we revise the cross tabulation, a useful summary for nominal data.
4
Outline
- First we revise the cross tabulation, a useful summary for nominal data.
- We then cover ways to visualise the information in a cross tab.
4
Outline
- First we revise the cross tabulation, a useful summary for nominal data.
- We then cover ways to visualise the information in a cross tab.
- Ultimately we will discuss Correspondence Analysis which can be applied to large tables.
4
Outline
- First we revise the cross tabulation, a useful summary for nominal data.
- We then cover ways to visualise the information in a cross tab.
- Ultimately we will discuss Correspondence Analysis which can be applied to large tables.
- We cover applications of Correspondence Analysis in the real world including with text data.
4
A basic analysis
5
Beer example
- A cross tab can be created in R using the
tablefunction. The input is either
6
Beer example
- A cross tab can be created in R using the
tablefunction. The input is either- A single matrix or data frame with 2 columns/variables
6
Beer example
- A cross tab can be created in R using the
tablefunction. The input is either- A single matrix or data frame with 2 columns/variables
- One vector for each variable
6
Beer example
- A cross tab can be created in R using the
tablefunction. The input is either- A single matrix or data frame with 2 columns/variables
- One vector for each variable
- The output is a table object.
6
Beer example
- A cross tab can be created in R using the
tablefunction. The input is either- A single matrix or data frame with 2 columns/variables
- One vector for each variable
- The output is a table object.
- Let’s try it with the Beer data which can be found on Moodle.
6
Beer example
- We look at two categorical variables
7
Beer example
- We look at two categorical variables
- Availabilty
- Light
7
Beer example
- We look at two categorical variables
- Availabilty
- Light
- The number of categories for availability is 2 (National/Regional)
7
Beer example
- We look at two categorical variables
- Availabilty
- Light
- The number of categories for availability is 2 (National/Regional)
- The number of categories for light is 2 (Light/non-light).
7
Doing it in R
load('Beer.RData')Beer %>% select(light,avail)%>% table%>% #Creates Tables addmargins()-> #Includes totals crosstab8
The table
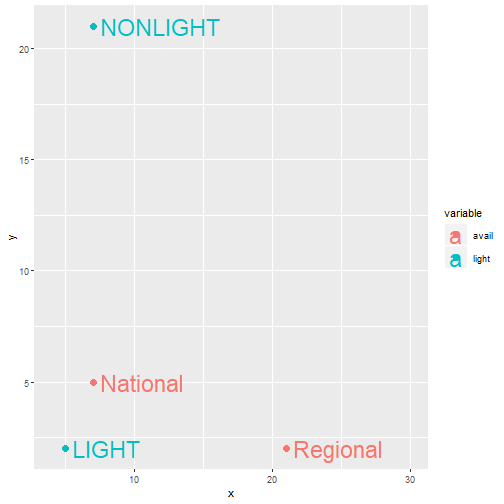
print(crosstab)## avail## light National Regional Sum## NONLIGHT 7 21 28## LIGHT 5 2 7## Sum 12 23 359
What do we see?
- There are more beers available at a regional level.
10
What do we see?
- There are more beers available at a regional level.
- The nationally available beers are just as likely to be light or non-light.
10
What do we see?
- There are more beers available at a regional level.
- The nationally available beers are just as likely to be light or non-light.
- Regional beers are overwhelmingly non-light.
10
What do we see?
- There are more beers available at a regional level.
- The nationally available beers are just as likely to be light or non-light.
- Regional beers are overwhelmingly non-light.
- But is there a way we can visualise this?
10
How to visualise?
- In this small example we can think of four sets of coordinates
11
How to visualise?
- In this small example we can think of four sets of coordinates
- Coordinates for national
11
How to visualise?
- In this small example we can think of four sets of coordinates
- Coordinates for national
- Coordinates for regional
11
How to visualise?
- In this small example we can think of four sets of coordinates
- Coordinates for national
- Coordinates for regional
- Coordinates for non-light
11
How to visualise?
- In this small example we can think of four sets of coordinates
- Coordinates for national
- Coordinates for regional
- Coordinates for non-light
- Coordinates for light
11
How to visualise?
- In this small example we can think of four sets of coordinates
- Coordinates for national
- Coordinates for regional
- Coordinates for non-light
- Coordinates for light
- Let's plot these
11
Plot
12
Summary
- Even on this very basic plot we can see an association between light beers and national availability
13
Summary
- Even on this very basic plot we can see an association between light beers and national availability
- However what do we do with
13
Summary
- Even on this very basic plot we can see an association between light beers and national availability
- However what do we do with
- Large cross tabulations
13
Summary
- Even on this very basic plot we can see an association between light beers and national availability
- However what do we do with
- Large cross tabulations
- Non-square cross tabulations
13
Summary
- Even on this very basic plot we can see an association between light beers and national availability
- However what do we do with
- Large cross tabulations
- Non-square cross tabulations
- To solve these issues Correspondence Analysis can be used. It is more complicated than simply plotting rows and columns in the cross tab
13
A Bigger Cross Tab
14
Breakfast example
- The table on the next slide is reproduced from Bendixen, M., (2003).
15
Breakfast example
- The table on the next slide is reproduced from Bendixen, M., (2003).
- Different breakfast foods (e.g. CER=cereal, MUE=muesli), with a total of 8 categories.
15
Breakfast example
- The table on the next slide is reproduced from Bendixen, M., (2003).
- Different breakfast foods (e.g. CER=cereal, MUE=muesli), with a total of 8 categories.
- Different attributes of those foods (‘Healthy’, ‘Economical’, ‘Tasteless’) with a total of 14 categories.
15
Breakfast example
- The table on the next slide is reproduced from Bendixen, M., (2003).
- Different breakfast foods (e.g. CER=cereal, MUE=muesli), with a total of 8 categories.
- Different attributes of those foods (‘Healthy’, ‘Economical’, ‘Tasteless’) with a total of 14 categories.
- Survey asked to match attributes to breakfasts.
15
Breakfast example
- The table on the next slide is reproduced from Bendixen, M., (2003).
- Different breakfast foods (e.g. CER=cereal, MUE=muesli), with a total of 8 categories.
- Different attributes of those foods (‘Healthy’, ‘Economical’, ‘Tasteless’) with a total of 14 categories.
- Survey asked to match attributes to breakfasts.
- A cross tab shows the frequency with which each food was matched to each attribute.
15
Breakfast example
| BE | CER | FRF | MUE | POR | STF | TT | YOG | |
|---|---|---|---|---|---|---|---|---|
| Economical | 3 | 24 | 7 | 3 | 20 | 3 | 16 | 7 |
| Expensive | 27 | 6 | 9 | 33 | 5 | 18 | 3 | 10 |
| Family Favourite | 31 | 14 | 7 | 4 | 10 | 2 | 5 | 5 |
| Healthy | 18 | 14 | 31 | 38 | 25 | 28 | 8 | 34 |
| Long Prepare | 35 | 0 | 0 | 0 | 9 | 10 | 1 | 0 |
| Nutritious | 25 | 14 | 32 | 28 | 25 | 26 | 7 | 31 |
| Quick | 2 | 54 | 26 | 33 | 8 | 8 | 15 | 20 |
| Summer | 13 | 42 | 37 | 22 | 11 | 16 | 7 | 35 |
| Tasteless | 2 | 8 | 0 | 6 | 2 | 2 | 0 | 1 |
| Tasty | 34 | 24 | 33 | 21 | 16 | 26 | 11 | 26 |
| Treat | 31 | 5 | 4 | 3 | 3 | 16 | 4 | 17 |
| Weekdays | 9 | 47 | 11 | 24 | 15 | 6 | 13 | 10 |
| Weekends | 56 | 12 | 10 | 5 | 8 | 23 | 16 | 18 |
| Winter | 26 | 10 | 11 | 10 | 32 | 19 | 6 | 8 |
16
Visualising this
We can visualise this using Correspondence Analysis which requires the ca package.
library(ca) caout<-ca(breakfastct) plot(caout) You need to install the ca package first
17
Visualising this
## Warning: package 'ca' was built under R version 3.6.2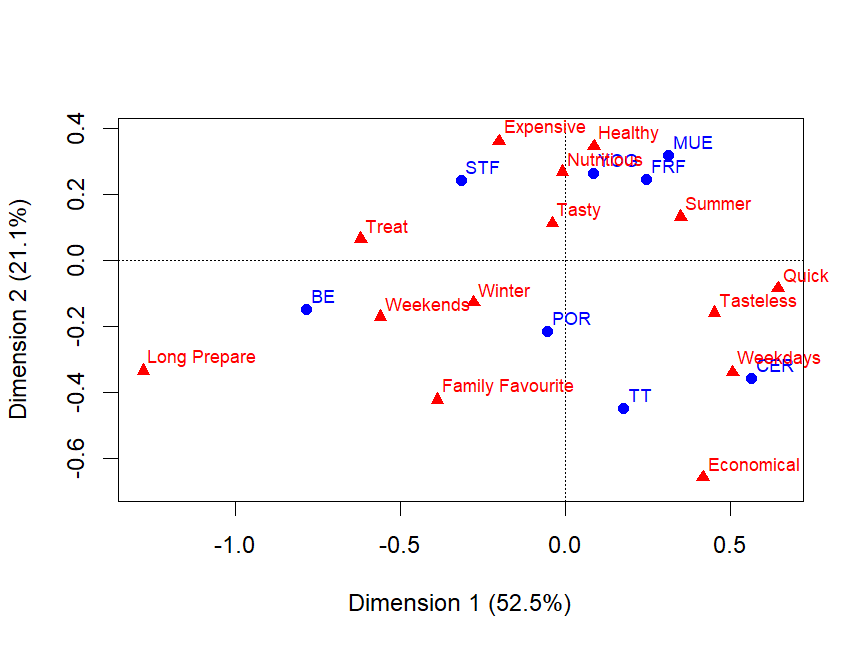
18
What can we see?
- Towards the top of the plot are categories like Expensive, Healthy and Nutritious. There are associated with Muesli (MUE) and Fresh Fruit(FRF).
19
What can we see?
- Towards the top of the plot are categories like Expensive, Healthy and Nutritious. There are associated with Muesli (MUE) and Fresh Fruit(FRF).
- The left of the plot has the catgeory Long Prepare, with Bacon and Eggs (BE) closest to this point.
19
What can we see?
- Towards the top of the plot are categories like Expensive, Healthy and Nutritious. There are associated with Muesli (MUE) and Fresh Fruit(FRF).
- The left of the plot has the catgeory Long Prepare, with Bacon and Eggs (BE) closest to this point.
- Cereal (CER) is associated with Weekdays.
19
What can we see?
- Towards the top of the plot are categories like Expensive, Healthy and Nutritious. There are associated with Muesli (MUE) and Fresh Fruit(FRF).
- The left of the plot has the catgeory Long Prepare, with Bacon and Eggs (BE) closest to this point.
- Cereal (CER) is associated with Weekdays.
- What else?
19
Correspondence Analysis
- The plot is easy to interpret. Categories that are close to one another on the plot have a strong association with one another.
20
Correspondence Analysis
- The plot is easy to interpret. Categories that are close to one another on the plot have a strong association with one another.
- This is the case when we compare
20
Correspondence Analysis
- The plot is easy to interpret. Categories that are close to one another on the plot have a strong association with one another.
- This is the case when we compare
- Two categories in the rows of the table,
20
Correspondence Analysis
- The plot is easy to interpret. Categories that are close to one another on the plot have a strong association with one another.
- This is the case when we compare
- Two categories in the rows of the table,
- Two categories in the column of the table,
20
Correspondence Analysis
- The plot is easy to interpret. Categories that are close to one another on the plot have a strong association with one another.
- This is the case when we compare
- Two categories in the rows of the table,
- Two categories in the column of the table,
- A category in the row of the cross tab with a category in the column of a cross tab
20
Correspondence Analysis
- The plot is easy to interpret. Categories that are close to one another on the plot have a strong association with one another.
- This is the case when we compare
- Two categories in the rows of the table,
- Two categories in the column of the table,
- A category in the row of the cross tab with a category in the column of a cross tab
- What about the remaining output?
20
Other output
summary(caout,row=FALSE,column=FALSE) ## ## Principal inertias (eigenvalues): ## ## dim value % cum% scree plot ## 1 0.193095 52.5 52.5 ************* ## 2 0.077731 21.1 73.6 ***** ## 3 0.043854 11.9 85.6 *** ## 4 0.032804 8.9 94.5 ** ## 5 0.012257 3.3 97.8 * ## 6 0.005687 1.5 99.4 ## 7 0.002363 0.6 100.0 ## -------- ----- ## Total: 0.367791 100.021
Connection to PCA/MDS
- There are similarities with material covered in PCA and MDS
22
Connection to PCA/MDS
- There are similarities with material covered in PCA and MDS
- We visualise with a biplot.
22
Connection to PCA/MDS
- There are similarities with material covered in PCA and MDS
- We visualise with a biplot.
- Terms such as eigenvalues and scree plot reappear.
22
Connection to PCA/MDS
- There are similarities with material covered in PCA and MDS
- We visualise with a biplot.
- Terms such as eigenvalues and scree plot reappear.
- In PCA/MDS the aim was to maximise variance or minimise strain.
22
Connection to PCA/MDS
- There are similarities with material covered in PCA and MDS
- We visualise with a biplot.
- Terms such as eigenvalues and scree plot reappear.
- In PCA/MDS the aim was to maximise variance or minimise strain.
- In CA the aim is to maximise inertia.
22
Inertia
- Categorical data are not ordinal.
23
Inertia
- Categorical data are not ordinal.
- We cannot measure dependence in categorical data by seeing whether 'large' values of one variable coincide with 'large' values of the other variable.
23
Inertia
- Categorical data are not ordinal.
- We cannot measure dependence in categorical data by seeing whether 'large' values of one variable coincide with 'large' values of the other variable.
- We cannot use correlation.
23
Inertia
- Categorical data are not ordinal.
- We cannot measure dependence in categorical data by seeing whether 'large' values of one variable coincide with 'large' values of the other variable.
- We cannot use correlation.
- Inertia is a measure of the dependence in categorical data, closely related to the chi square statistic from a test of independence between two categorical variables.
23
Inertia
- Categorical data are not ordinal.
- We cannot measure dependence in categorical data by seeing whether 'large' values of one variable coincide with 'large' values of the other variable.
- We cannot use correlation.
- Inertia is a measure of the dependence in categorical data, closely related to the chi square statistic from a test of independence between two categorical variables.
- Let us quickly revise this.
23
Chi Square test
- Suppose we have two variables
24
Chi Square test
- Suppose we have two variables
- Variable 1 has two categories A and B
24
Chi Square test
- Suppose we have two variables
- Variable 1 has two categories A and B
- Variable 2 has two categories X and Y
24
Chi Square test
- Suppose we have two variables
- Variable 1 has two categories A and B
- Variable 2 has two categories X and Y
- Assume Variable 1 and 2 are independent
24
Chi Square test
- Suppose we have two variables
- Variable 1 has two categories A and B
- Variable 2 has two categories X and Y
- Assume Variable 1 and 2 are independent
- On the next slide we will have an incomplete cross tab
24
Cross Tab
| V1 \ V2 | X | Y | Total |
|---|---|---|---|
| A | 50 | ||
| B | 50 | ||
| Total | 20 | 80 | 100 |
If variable 1 and variable 2 are independent then what numbers do you expect to be in the empty cells?
25
Cross Tab
| V1 \ V2 | X | Y | Total |
|---|---|---|---|
| A | 10 | 40 | 50 |
| B | 10 | 40 | 50 |
| Total | 20 | 80 | 100 |
Under independence
- Pr(A,X)=Pr(A)Pr(X)
- Pr(B,X)=Pr(B)Pr(X)
- Pr(A,Y)=Pr(A)Pr(Y)
- Pr(B,Y)=Pr(B)Pr(Y)
26
Independence is boring
- Independence is not interesting.
27
Independence is boring
- Independence is not interesting.
- We cannot draw any conclusions about association between categories across different variables.
27
Independence is boring
- Independence is not interesting.
- We cannot draw any conclusions about association between categories across different variables.
- If we were to do the crude plot from the beer example, all points would lie in the same direction.
27
Independence is boring
- Independence is not interesting.
- We cannot draw any conclusions about association between categories across different variables.
- If we were to do the crude plot from the beer example, all points would lie in the same direction.
- In correspondence analysis, for perfect independence all row and column categories fall on a single point.
27
Random variation
- Even for independence, due to randomness we may actually get a table like this:
| V1 \ V2 | X | Y | Total |
|---|---|---|---|
| A | 12 | 38 | 50 |
| B | 8 | 42 | 50 |
| Total | 20 | 80 | 100 |
- How do we know whether the variables are truly independent and not due to random variation?
28
The chi square test
For the chi square test, in each cell we compute
(Oij−Eij)2Eij
where Oij is the observed count in each cell and Eij is the expected count in each cell.
29
Chi Square Statistic
The chi square statistic is
χ2=r∑i=1c∑j=1(Oij−Eij)2Eij
where r and c are the number of rows and columns in the cross tab respectively.
30
The chi square test
- If the variables are truly independent then it is unlikely that one would observe large values of χ2
31
The chi square test
- If the variables are truly independent then it is unlikely that one would observe large values of χ2
- In this case we reject the null and conclude the variables are dependent.
31
The chi square test
- If the variables are truly independent then it is unlikely that one would observe large values of χ2
- In this case we reject the null and conclude the variables are dependent.
- However, we can also think of the χ2 stat as a measure of dependence where:
31
The chi square test
- If the variables are truly independent then it is unlikely that one would observe large values of χ2
- In this case we reject the null and conclude the variables are dependent.
- However, we can also think of the χ2 stat as a measure of dependence where:
- Small values indicate low dependence
- Large values indicate high dependence
31
Inertia
- Correspondence analysis is based on a similar idea.
32
Inertia
- Correspondence analysis is based on a similar idea.
- However the counts in each cell Oi and Ei are replaced with probabilities oij=Oijn and eij=Eij/n.
32
Inertia
- Correspondence analysis is based on a similar idea.
- However the counts in each cell Oi and Ei are replaced with probabilities oij=Oijn and eij=Eij/n.
- Each count is dividided by n which is the total of all cell counts (i.e. r×c).
32
Inertia
- Correspondence analysis is based on a similar idea.
- However the counts in each cell Oi and Ei are replaced with probabilities oij=Oijn and eij=Eij/n.
- Each count is dividided by n which is the total of all cell counts (i.e. r×c).
- Instead of the χ2 we get inertia defined as Inertia=χ2n
32
Correspondence Analysis
- Correspondence analysis is about explaining as much inertia as possible with a small number of dimensions.
33
Correspondence Analysis
- Correspondence analysis is about explaining as much inertia as possible with a small number of dimensions.
- Instead of the original rows and columns in the cross tab, a small number of linear combinations of these rows and columns are formed.
33
Correspondence Analysis
- Correspondence analysis is about explaining as much inertia as possible with a small number of dimensions.
- Instead of the original rows and columns in the cross tab, a small number of linear combinations of these rows and columns are formed.
- A good approximation to the original cross tab could be be reconstructed from these linear combinations.
33
Geometric Interpretation
- Each column category can be plotted in r-dimensions.
34
Geometric Interpretation
- Each column category can be plotted in r-dimensions.
- Each row category can be plotted in c-dimensions.
34
Geometric Interpretation
- Each column category can be plotted in r-dimensions.
- Each row category can be plotted in c-dimensions.
- Correspondence Analysis rotates both of these to provide the most interesting 'optimal' 2D visualisation
34
Geometric Interpretation
- Each column category can be plotted in r-dimensions.
- Each row category can be plotted in c-dimensions.
- Correspondence Analysis rotates both of these to provide the most interesting 'optimal' 2D visualisation
- Here 'optimal' refers to maximising inertia.
34
Back to the output
summary(caout,row=FALSE,column=FALSE) ## ## Principal inertias (eigenvalues): ## ## dim value % cum% scree plot ## 1 0.193095 52.5 52.5 ************* ## 2 0.077731 21.1 73.6 ***** ## 3 0.043854 11.9 85.6 *** ## 4 0.032804 8.9 94.5 ** ## 5 0.012257 3.3 97.8 * ## 6 0.005687 1.5 99.4 ## 7 0.002363 0.6 100.0 ## -------- ----- ## Total: 0.367791 100.035
How to intepret this
- Eigenvalues previously told us:
36
How to intepret this
- Eigenvalues previously told us:
- The variance explained by each principal component in PCA.
36
How to intepret this
- Eigenvalues previously told us:
- The variance explained by each principal component in PCA.
- Give some indication of the Goodness of fit for MDS.
36
How to intepret this
- Eigenvalues previously told us:
- The variance explained by each principal component in PCA.
- Give some indication of the Goodness of fit for MDS.
- In CA the eigenvalues tell us the proportion of inertia explained by the solution.
36
How to intepret this
- Eigenvalues previously told us:
- The variance explained by each principal component in PCA.
- Give some indication of the Goodness of fit for MDS.
- In CA the eigenvalues tell us the proportion of inertia explained by the solution.
- A 2D solution is usually used for visualisation.
36
How to intepret this
- Eigenvalues previously told us:
- The variance explained by each principal component in PCA.
- Give some indication of the Goodness of fit for MDS.
- In CA the eigenvalues tell us the proportion of inertia explained by the solution.
- A 2D solution is usually used for visualisation.
- In the breakfast example the visualisation explains 73.6% of the inertia.
36
Matrix decompositions
37
Matrix decompositions
- Wherever dimension reduction is used there is usually a matrix decomposition hidden somewhere.
38
Matrix decompositions
- Wherever dimension reduction is used there is usually a matrix decomposition hidden somewhere.
- In this case, the matrix that is decomposed is related to the cross tab.
38
Matrix decompositions
- Wherever dimension reduction is used there is usually a matrix decomposition hidden somewhere.
- In this case, the matrix that is decomposed is related to the cross tab.
- In particular consider the values
mij=oij−eij√eij
38
What about CA?
- Now consider a matrix M with mij in the ith row and jth column.
39
What about CA?
- Now consider a matrix M with mij in the ith row and jth column.
- Let the SVD of this matrix be M=UDV′
39
What about CA?
- Now consider a matrix M with mij in the ith row and jth column.
- Let the SVD of this matrix be M=UDV′
- We will consider
39
What about CA?
- Now consider a matrix M with mij in the ith row and jth column.
- Let the SVD of this matrix be M=UDV′
- We will consider
- Post-multiplying by V
- Pre-multiplying by U′
39
Post-multiplying by V
- This gives UDV′V=UD
40
Post-multiplying by V
- This gives UDV′V=UD
- We get a factor score for each row category that is a linear combination of all column categories.
40
Post-multiplying by V
- This gives UDV′V=UD
- We get a factor score for each row category that is a linear combination of all column categories.
- These are a bit like principal components for the row categories.
40
Pre-multiplying by U′
- This gives U′UDV′=DV′
41
Pre-multiplying by U′
- This gives U′UDV′=DV′
- We get a factor score for each column category that is a linear combination of all row categories.
41
Pre-multiplying by U′
- This gives U′UDV′=DV′
- We get a factor score for each column category that is a linear combination of all row categories.
- These are a bit like principal components for the column categories.
41
On the same plot
- All the information can be summarised in a single plot using the biplot
42
On the same plot
- All the information can be summarised in a single plot using the biplot
- For CA the symmetric normalisation is often used.
42
On the same plot
- All the information can be summarised in a single plot using the biplot
- For CA the symmetric normalisation is often used.
- This means we plot the first two columns of UD1/2 and VD1/2
42
On the same plot
- All the information can be summarised in a single plot using the biplot
- For CA the symmetric normalisation is often used.
- This means we plot the first two columns of UD1/2 and VD1/2
- This way we do not prioritise a more accurate representation neither for rows nor for columns.
42
Application
43
Example: Hotel Reviews
- For an interesting example related to marketing consider hotel reviews.
44
Example: Hotel Reviews
- For an interesting example related to marketing consider hotel reviews.
- Many websites provide user reviews.
44
Example: Hotel Reviews
- For an interesting example related to marketing consider hotel reviews.
- Many websites provide user reviews.
- The words in each review can be scraped from the web
44
Example: Hotel Reviews
- For an interesting example related to marketing consider hotel reviews.
- Many websites provide user reviews.
- The words in each review can be scraped from the web
- In the following example eight hotels in Melbourne were considered
44
Example: Hotel Reviews
- For an interesting example related to marketing consider hotel reviews.
- Many websites provide user reviews.
- The words in each review can be scraped from the web
- In the following example eight hotels in Melbourne were considered
- Four that were highly rated: Crown Towers, Adelphi, Larwill and QT
44
Example: Hotel Reviews
- For an interesting example related to marketing consider hotel reviews.
- Many websites provide user reviews.
- The words in each review can be scraped from the web
- In the following example eight hotels in Melbourne were considered
- Four that were highly rated: Crown Towers, Adelphi, Larwill and QT
- Four that were not highly rated: Mercure, FlagstaffCity, Citiclub, Hotel Sophia
44
Example: Hotel Reviews
- For each hotel, 100 reviews were scraped.
45
Example: Hotel Reviews
- For each hotel, 100 reviews were scraped.
- So called stop words ('the', 'a', 'is') were removed as were the names of the hotels.
45
Example: Hotel Reviews
- For each hotel, 100 reviews were scraped.
- So called stop words ('the', 'a', 'is') were removed as were the names of the hotels.
- The 20 most frequent words used for each hotel.
45
Example: Hotel Reviews
- For each hotel, 100 reviews were scraped.
- So called stop words ('the', 'a', 'is') were removed as were the names of the hotels.
- The 20 most frequent words used for each hotel.
- Combining these lists for 8 hotels led to 63 words (some words appear on multiple top 20 lists)
45
Example: Hotel Reviews
- Jaccard similarity could be used to do MDS
46
Example: Hotel Reviews
- Jaccard similarity could be used to do MDS
- However there are two interesting things that will not be captured by such an analysis
46
Example: Hotel Reviews
- Jaccard similarity could be used to do MDS
- However there are two interesting things that will not be captured by such an analysis
- The frequency with which words appear is important.
46
Example: Hotel Reviews
- Jaccard similarity could be used to do MDS
- However there are two interesting things that will not be captured by such an analysis
- The frequency with which words appear is important.
- The association between the hotels and words.
46
Example: Hotel Reviews
- On Moodle you will find a cross tab featuring the frequency with which each word appeared on each review
Adelphi Citiclub CrownTowers FlagstaffCity HotelSophia Larwill Mercure QT amazing 24 1 24 1 0 15 1 33 bar 13 4 1 1 2 5 8 48 bathroom 3 7 8 6 14 4 19 6 bed 13 11 3 9 15 25 19 19 booked 6 21 9 15 10 1 5 1 breakfast 5 5 6 6 17 5 9 9 city 15 4 17 17 9 17 11 12 clean 8 22 7 32 37 21 19 7 close 11 9 2 14 11 12 17 7 club 1 64 25 0 0 0 0 0 comfortable 15 4 17 6 17 24 20 27 cross 0 0 0 2 18 0 0 0 crown 0 0 89 0 0 0 0 2 crystal 0 0 24 0 0 0 0 0 dear 97 0 47 0 0 6 41 0 enjoyed 28 51 18 1 2 20 8 46 experience 36 2 18 1 3 11 11 39 fantastic 46 4 10 1 1 17 5 21 feedback 32 66 17 0 1 6 15 39 forward 1 51 5 0 0 4 13 4 free 10 4 2 14 14 6 5 2 friendly 23 17 16 9 9 30 19 35 good 12 67 9 21 29 21 27 14 great 71 76 31 14 19 52 19 95 hear 23 7 32 1 3 17 9 44 hello 1 0 0 0 0 9 0 62 helpful 13 12 4 9 7 26 15 16 hi 0 0 0 0 0 23 1 29 hotel 74 172 49 32 61 51 65 67 leave 41 2 5 2 0 11 1 14 location 51 25 17 10 28 26 19 35 lovely 21 2 10 0 1 31 3 30 melbourne 36 7 49 22 28 19 26 77 much 45 61 11 4 8 18 3 40 my 26 15 40 17 21 28 26 27 night 18 53 16 26 17 8 14 13 nights 7 27 8 16 9 10 14 4 noise 2 64 0 3 5 1 6 1 north 0 0 1 0 0 1 25 0 old 1 0 0 6 5 0 21 3 park 0 0 0 2 0 24 1 1 parking 2 2 5 18 2 15 13 2 place 9 10 9 17 12 9 8 11 positive 1 55 7 1 1 9 2 6 really 13 10 5 4 11 21 3 43 receive 1 55 2 0 0 0 0 0 reception 0 4 6 7 27 5 9 3 review 49 98 39 1 1 37 23 32 room 34 61 70 59 81 64 61 51 rooms 30 53 23 31 10 34 33 35 service 41 57 30 2 9 10 16 40 southern 0 0 0 2 18 0 0 0 staff 72 25 35 26 25 44 41 76 station 1 2 0 4 21 0 0 0 stay 86 100 71 24 21 60 58 66 stayed 21 32 33 31 21 26 29 23 taking 61 99 7 1 0 15 21 37 team 44 0 21 0 0 3 9 8 thank 89 127 51 0 0 38 27 44 time 86 99 15 5 9 36 29 51 towers 0 0 69 0 0 0 0 1 walk 5 2 5 13 14 5 5 4 wonderful 48 2 16 1 1 11 4 27
47
Example: Hotel Reviews
The data can be loaded and correspondence analysis can be carried out using
load('hotels.RData') hoteltable%>%ca%>%plot48
Example: Hotel Reviews
49
Conclusions
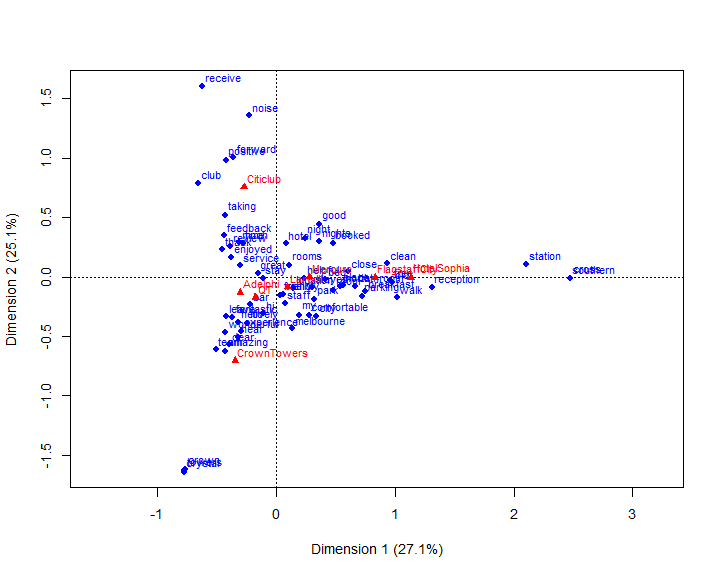
- Towards the bottom left of the plot are words like wonderful, amazing and fantastic.
50
Conclusions
- Towards the bottom left of the plot are words like wonderful, amazing and fantastic.
- The more highly rated hotels Crown Towers, QT and Adelphi are closer towards the bottom left
50
Conclusions
- Towards the bottom left of the plot are words like wonderful, amazing and fantastic.
- The more highly rated hotels Crown Towers, QT and Adelphi are closer towards the bottom left
- Towards the top of the plot the words noise and club appear together with the Citiclub hotel
50
Conclusions
- Towards the bottom left of the plot are words like wonderful, amazing and fantastic.
- The more highly rated hotels Crown Towers, QT and Adelphi are closer towards the bottom left
- Towards the top of the plot the words noise and club appear together with the Citiclub hotel
- This suggests that there may be complaints about noise from a night club.
50
Conclusions
- Towards the right of the plot the word old appears as does Hotel Sophia and Flagstaff
51
Conclusions
- Towards the right of the plot the word old appears as does Hotel Sophia and Flagstaff
- These are lower rated hotels, the age of the hotels may be a problem.
51
Conclusions
- Towards the right of the plot the word old appears as does Hotel Sophia and Flagstaff
- These are lower rated hotels, the age of the hotels may be a problem.
- Can you see anything else?
51
Example: Hotel Reviews
## ## Principal inertias (eigenvalues): ## ## dim value % cum% scree plot ## 1 0.199004 27.1 27.1 ******* ## 2 0.184450 25.1 52.2 ****** ## 3 0.155095 21.1 73.3 ***** ## 4 0.075622 10.3 83.6 *** ## 5 0.058206 7.9 91.5 ** ## 6 0.038432 5.2 96.7 * ## 7 0.024115 3.3 100.0 * ## -------- ----- ## Total: 0.734923 100.052
Example: Hotel Reviews
You must enable Javascript to view this page properly.
53
Critique of the Analysis
- Together the first two dimensions only explain slightly more than half of the inertia (52.2%)
54
Critique of the Analysis
- Together the first two dimensions only explain slightly more than half of the inertia (52.2%)
- This suggests a large proportion of dependence is not explained by the plot
54
Critique of the Analysis
- Together the first two dimensions only explain slightly more than half of the inertia (52.2%)
- This suggests a large proportion of dependence is not explained by the plot
- Counting the frequency of words can be problematic.
54
Critique of the Analysis
- Together the first two dimensions only explain slightly more than half of the inertia (52.2%)
- This suggests a large proportion of dependence is not explained by the plot
- Counting the frequency of words can be problematic.
- Consider clean v not clean.
54
Critique of the Analysis
- Together the first two dimensions only explain slightly more than half of the inertia (52.2%)
- This suggests a large proportion of dependence is not explained by the plot
- Counting the frequency of words can be problematic.
- Consider clean v not clean.
- Also some aspects of the analysis are quite crude. Why use top 20 words? Why not 100?
54
Critique of the Analysis
- Together the first two dimensions only explain slightly more than half of the inertia (52.2%)
- This suggests a large proportion of dependence is not explained by the plot
- Counting the frequency of words can be problematic.
- Consider clean v not clean.
- Also some aspects of the analysis are quite crude. Why use top 20 words? Why not 100?
- More words more difficult to visualise.
54
Summary
- Main things to know
55
Summary
- Main things to know
- CA used for categorical data.
55
Summary
- Main things to know
- CA used for categorical data.
- Used to visualise two variable with many categories.
55
Summary
- Main things to know
- CA used for categorical data.
- Used to visualise two variable with many categories.
- Aim is to maximise proportion of explained inertia.
55
Summary
- Main things to know
- CA used for categorical data.
- Used to visualise two variable with many categories.
- Aim is to maximise proportion of explained inertia.
- Know how can it be used in practice.
55