Probabilistic Forecast Reconciliation: Properties, Evaluation and Score Optimisation

Abstract

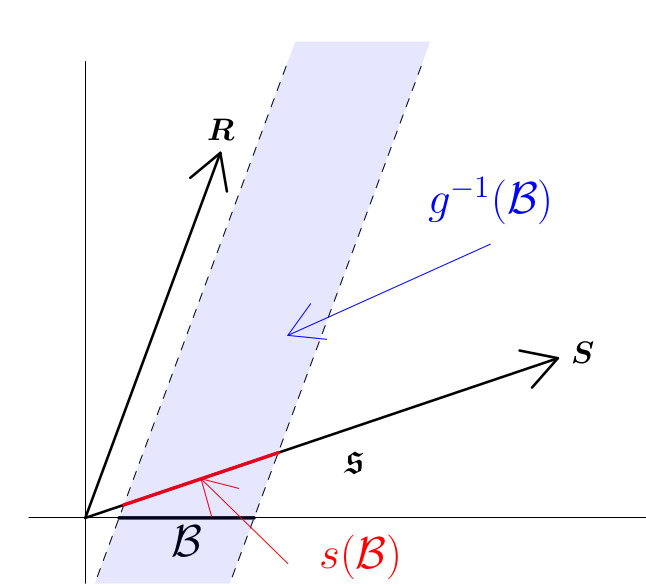
We develop a framework for prediction of multivariate data that follow some known linear constraints, such as the example where some variables are aggregates of others. This is particularly common when forecasting time series (predicting the future), but also arises in other types of prediction. For point prediction, an increasingly popular technique is reconciliation, whereby predictions are made for all series (so-called ‘base’ predictions) and subsequently adjusted to ensure coherence with the constraints. This paper extends reconciliation from the setting of point prediction to probabilistic pre- diction. A novel definition of reconciliation is developed and used to construct densities and draw samples from a reconciled probabilistic prediction. In the elliptical case, it is proven that the true predictive distribution can be recovered from reconciliation even when the location and scale matrix of the base prediction are chosen arbitrarily. To find reconciliation weights, an objective function based on scoring rules is optimised. The energy and variogram scores are considered since the log score is improper in the context of comparing unreconciled to reconciled predictions, a result also proved in this paper. To account for the stochastic nature of the energy and variogram scores, optimisation is achieved using stochastic gradient descent. This method is shown to improve base predictions in simulation studies and in an empirical application, particu- larly when the base prediction models are severely misspecified. When misspecification is not too severe, extending popular reconciliation methods for point prediction can result in a similar performance to score optimisation via stochastic gradient descent. The methods described here are implemented in the ProbReco package for R.

Anastasios N. Panagiotelis

Associate Professor of Business Analytics

My research interests include applied statistics and data science.